slam14讲之李群李代数

1.李群和李代数

1.R和ϕ的关系

R是随着时间t变化的且R * RT = I，因此对时间t求导，得到反对称矩阵。因此根据反对称矩阵找到一个对应R的向量

李代数的引出是根据旋转对时间求导，根据R矩阵的正交性会得到一个反对称矩阵。根据之前的知识我们知道反对称矩阵可以用 一个向量加上反对称符合表示 这样就把三维空间R和二维向量Φ联系起来。同时我们会知道 二维的是三维的一个映射 ，映射关系服从指数映射

我们上面知道了 如何从一个Φ 推导出R 符合罗德里公式 ，因次Φ = Θα 也可以根据迹的公式和关系 分解得到两个变量

同时我们把R(t)利用导数定义展开的时候可以得到定义式：

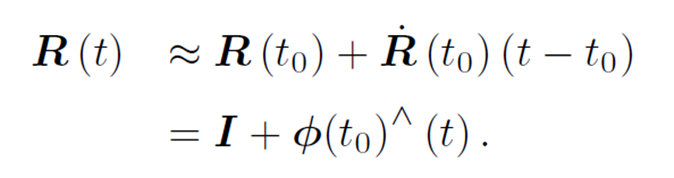
在t0附近，

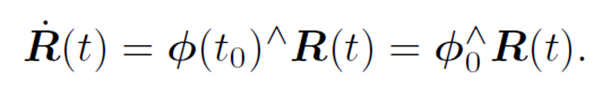
利用微分方程求解

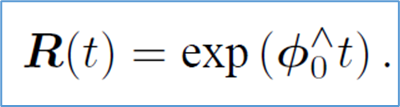
总结：ϕ描述的是R在某个局部的导数关系， 这就是指数对数的映射关系。

2.指数映射

3.扰动模型

1.

在SLAM问题中，待求解的变量都是位姿（较上个状态的旋转，平移），而一般采取优化的方法来求出待解变量。而优化的问题中，导数是非常重要的消息。https://zhuanlan.zhihu.com/p/504777287

因此在按照一般的导数定义求导的时候，预求f(x)在某点x0的导数，需要给x0增加一个微小量 Δx 。按照这想法，把微小量 当作一个微小的旋转量，左乘或者右乘到f(x)上，这也也可以得到导数，这也的思想是扰动模型。

而如何处理两个exp(ϕ^)【也就是R】相乘的时候的计算问题，这就是BCH公式 ：说明了R左乘或者右乘微小旋转后李代数上的表达。同时李群上不能相加，李代数上能相加，在李代数上相加也可以转换为李群上对R的左乘或者右乘的形式。

2.

矩阵的指数运算并不满足标量的运算公式，满足是BCH公式

R矩阵的乘法 在指数运算上可以符合一些向量的运算公式

引出 我们一般需要对T进行求导，而李群不满足 加法 李代数满足加法

因此有两种想法 利用李代数 加一个微小变量，进行导数定义

另一个就是左乘微小扰动 （相当于李代数加法） 对扰动求导

在本章之后构造的误差函数，对自变量是不方便直接求导的，因此对自变量进行小量扰动，然后求出对小量的偏导，令其为0，得到小量，再把自变量加上小量，进行更新，进行下一轮的迭代。

3

另一种思想，高博ppt上说的

由于R没有加法，导数无从定义

存在两种解决办法：

对 R 对应的李代数加上小量，求相对于小量的变化率（导数模型）；

对 R 左乘或右乘一个小量，求相对于小量的李代数的变化率（扰动模型）。

总结，微小扰动求导是一种方法，因为可能想的是其实对R*ΔR就相当于再exp(ϕ^ + Jr^-1(ϕ^)*ϕ2^）可以把右侧的当作一个小量t 其实和导数定义差不多的意思。