CVPR2020 | PoTrip | 迈向可迁移目标性攻击

---

论文链接

本文 “Towards Transferable Targeted Attack” 聚焦于深度学习中可迁移的目标性攻击这一关键问题。深度神经网络虽应用广泛，但对抗样本的存在威胁其安全，现有方法在生成可迁移的目标性对抗样本方面存在不足。该研究发现传统方法存在梯度衰减致噪声固化和未充分利用真实标签信息等问题，并提出创新方法。通过在 ImageNet 数据集上对多种先进网络进行实验，结果表明该方法在白盒和黑盒攻击中成功率显著高于现有方法，为提升神经网络对抗攻击的安全性提供了重要思路。

---

摘要-Abstract

An intriguing property of adversarial examples is their transferability, which suggests that black-box attacks are feasible in real-world applications. Previous works mostly study the transferability on non-targeted setting. However, recent studies show that targeted adversarial examples are more difficult to transfer than non-targeted ones. In this paper, we find there exist two defects that lead to the difficulty in generating transferable examples. First, the magnitude of gradient is decreasing during iterative attack, causing excessive consistency between two successive noises in accumulation of momentum, which is termed as noise curing. Second, it is not enough for targeted adversarial examples to just get close to target class without moving away from true class. To overcome the above problems, we propose a novel targeted attack approach to effectively generate more transferable adversarial examples. Specifically, we first introduce the Poincar ́e distance as the similarity metric to make the magnitude of gradient self-adaptive during iterative attack to alleviate noise curing. Furthermore, we regularize the targeted attack process with metric learning to take adversarial examples away from true label and gain more transferable targeted adversarial examples. Experiments on ImageNet validate the superiority of our approach achieving 8% higher attack success rate over other state-of-the-art methods on average in black-box targeted attack.

对抗样本的一个有趣特性是它们的可迁移性，这表明黑盒攻击在现实应用中是可行的。先前的工作大多研究非目标设定下的可迁移性。然而，最近的研究表明，目标性的对抗样本比非目标性的更难迁移。在本文中，我们发现存在两个导致生成可迁移样本困难的缺陷。首先，在迭代攻击过程中梯度的幅值会减小，这使得在动量积累过程中连续两个噪声之间过度一致，这种现象被称为噪声固化。其次，对于目标性的对抗样本来说，仅仅接近目标类别而不远离真实类别是不够的。为了克服上述问题，我们提出了一种新的目标性的攻击方法，以有效地生成更具可迁移性的对抗样本。具体来说，我们首先引入庞加莱距离作为相似性度量，使迭代攻击过程中的梯度幅值自适应，以缓解噪声固化。此外，我们利用度量学习对目标性的攻击过程进行正则化，使对抗样本远离真实标签，从而获得更具可迁移性的目标性的对抗样本。 在 ImageNet 上的实验验证了我们的方法的优越性，在黑盒有目标性攻击中，我们的方法比其他最先进的方法平均攻击成功率高出 8%.

---

引言-Introduction

深度学习在各领域取得成功的同时，深度神经网络（DNNs）的稳健性与安全性备受关注，因对抗样本问题使其面临安全隐患，促使众多对抗攻击方法涌现以评估和提升其稳健性。

• 攻击方法分类及特性：攻击方法依对抗特异性分为非目标性和目标性攻击两类。非目标性攻击期望对抗样本预测为除原类别外的任意类别，部分方法生成的此类样本跨模型迁移性强，引发黑盒攻击安全问题；目标性攻击要求样本被误判为特定类别，但现有多数方法侧重目标性攻击，针对黑盒的目标性攻击方法效果不佳，简单扩展非目标性攻击方法无法有效利用目标性攻击特性，致使生成样本迁移性差。
• 本文研究动机与贡献：发现现有黑盒目标性攻击方法存在梯度幅值下降致噪声固化和未利用真实标签信息两大缺陷。为解决这些问题，首次引入Poincaré空间作为度量空间，并通过新的三元组损失利用真实标签信息。主要贡献包括：重新审视目标性攻击特性开发新方法；识别并解决噪声固化问题；利用真实标签信息生成样本；通过实验证明方法在目标性攻击中优于现有方法。

---

背景-Background

对抗攻击方法

• 基本原理：在对抗攻击中，对于给定的分类器$f(x)$，目标是找到一个小扰动$\delta$，满足$\Vert \delta {\Vert }_{\infty }\le ϵ$，使得$f(x^{adv})\ne y$，其中$x^{adv}=x+\delta$，通常通过最大化交叉熵损失来求解。
• 黑盒攻击：解决上述优化问题若需计算损失函数对输入的梯度则为白盒攻击，如 L - BFGS 虽能生成对抗样本但耗时不实用，FGSM 利用输入梯度符号学习对抗样本。在无法获取梯度的黑盒攻击场景下，因对抗样本的迁移性可将白盒攻击转化，为此提出系列方法提升迁移性。如 MI - FGSM 集成动量项使噪声添加方向更平滑；$D{I}^2$ - FGSM 以一定概率变换图像缓解过拟合；TI - FGSM 用未平移图像梯度卷积近似优化平移图像扰动，这些方法能生成有效的黑盒对抗样本。
• 目标性攻击：在多类分类问题中，与非目标性攻击不同，需目标模型输出特定目标标签。虽已有研究表明可迁移的非目标性对抗样本易找，但先前方法生成的目标性对抗样本难迁移，虽有将非目标性攻击方法扩展的尝试，但仍缺乏有效生成能欺骗黑盒模型的目标性对抗样本的方法，尤其对于对抗训练模型。

Poincaré 球

Poincaré球是一种典型的双曲空间，在几何性质上与欧几里得空间存在显著差异。在 Poincaré球中，如图 1（a） 所示，存在通过点 P 且不与直线 R 相交的不同直线，并且其内部的弧线永远不会到达球的圆周。这类似于双曲面上的测地线延伸至无穷远，意味着当点朝着 Poincaré球的表面移动时，其表面上的距离相对于欧几里得距离呈指数增长。

从表示能力来看，Poincaré球能够在单位球内拟合整个几何结构，相比欧几里得表示具有更高的容量。这一特性使其在计算机视觉任务的度量学习和表示学习领域引起了广泛关注，尤其是在处理复杂数据分布方面具有潜在优势。

Poincaré球内所有点都位于 n 维单位${\ell }_2$球内，任意两点 u 和 v（满足${\ell }_2$范数小于 1）之间的距离定义为$d(u,v)=\text{arccosh}(1+\delta (u,v))$，其中$\delta (u,v)=2\frac{\Vert u-v{\Vert }^2}{(1-\Vert u{\Vert }^2)(1-\Vert v{\Vert }^2)}$。从 图 1（b） 可以观察到，任何点到 Poincaré球边缘的距离趋近于无穷大。并且如 图 1（c） 所示，当点接近球表面时，Poincaré距离的增长幅度会急剧增大，这表明在该区域内梯度的幅值会随着向表面靠近而增加，这种独特的距离度量和梯度变化特性为后续在对抗攻击方法中的应用奠定了基础。

图 1：（a）：庞加莱球中的直线由球内所有与球边界正交的欧几里得弧线以及圆盘的所有直径组成。给定直线 R 的平行线可能在点 P 相交。（b）：庞加莱球模型的高容量。此图中每条线的长度相同。（c）：相对于欧几里得距离和 v 的范数，$d(u,v)$的增长情况，$\Vert u{\Vert }^2=0.98$

---

方法-Methodology

动机-Motivations

• 与非目标性攻击的关键差异未被利用：目标性攻击与非目标性攻击存在两个关键区别，但现有方法未有效利用。一是目标性攻击有目标，需找到对抗样本的（局部）最小点，而非目标性攻击只需避开局部极大值并远离判别边界；二是目标性攻击要确保对抗样本既不像原类别又更接近目标类别，但现有方法在这两方面表现不佳，导致迁移性差。
• 交叉熵损失引发的噪声固化问题：现有多数方法用交叉熵作损失函数，在目标性攻击的迭代过程中，其梯度与预测概率 $p_i$ 呈线性关系且单调递减，致使梯度在迭代中趋于消失。如 MI - FGSM 虽对梯度重缩放，但未考虑实际梯度大小，导致在目标类附近，因动量积累使连续噪声方向相似，产生噪声固化现象。这在非目标性攻击中有助于远离判别边界，但在目标性攻击中不利于找到目标类最小值，且当目标类概率接近 1 时，因 softmax 饱和，梯度变化小，若最后几次迭代梯度方向不当会积累误差。
• 对原标签信息的忽视：传统方法只关注最大化目标类概率，忽略对抗样本与原标签的距离。实验表明，这些方法在白盒环境下虽有效，但在目标攻击中，目标性对抗样本难以与真实类别分离，而原标签信息长期被忽视，因此有必要利用原标签生成更强大的目标性对抗样本。

图2：两类情况（(t = 1)，(t = 2)）下softmax输出(P(t = 1 | z))的概率。当(P(t = 1 | z))趋近于1时，它随(z)的变化缓慢。

图3：在MI - FGSM和基于庞加莱（Poincaré）攻击中，连续两次扰动的余弦相似度以及相应的目标类概率。为避免选择性呈现数据，结果是在包含1000个样本的公开ImageNet兼容数据集中的前10张图像上取平均值得到的。

图4：对来自同一真实类别但被误分类为目标类别的对抗图像进行t-SNE可视化。在没有三元组损失的情况下，将对抗样本与相应的真实类别区分开来更困难。

利用庞加莱距离度量的目标性攻击-Targeted Attack with Poincar´e Distance Metric

该部分主要围绕利用 Poincaré 距离度量改进目标攻击展开。

• 考虑到标签的 one - hot 编码向量 $y$ 满足 ${\sum }_i{y}_i=1$ 且 $\Vert y{\Vert }_2=1$，这表明 $y$ 处于 Poincaré 球的边缘，其到任何点的距离为 $+\infty$。在目标攻击中，需要降低模型 logits 与目标类的距离，而根据 Poincaré 球的性质，越靠近边界，梯度值越大。

• 直接使用 Poincaré 距离存在一个关键问题，即融合的 logits 不满足 $\Vert l(x){\Vert }_2<1$。为解决此问题，文中采用 ${\ell }_1$ 距离对 logits 进行归一化处理。同时，由于目标标签到任何点的距离为 $+\infty$ 会导致优化困难，因此参考已有方法，从目标标签 $y$ 中减去一个小常数 $\xi =0.0001$.

• 定义了 Poincaré 距离度量损失 ${\mathcal{L}}_{Po}(x,y)=d(u,v)=\text{arccosh}(1+\delta (u,v))$，其中 $u=l_k(x)/{\Vert l_k(x)\Vert }_1$， v = max ⁡ { y − ξ , 0 } v=\max\{y-\xi,0\} v=max{y−ξ,0}，这里的 $l(x)$ 是通过融合多个模型的 logits 得到的，具体为 $l(x)={\sum }_{k=1}^K{w}_k{l}_k(x)$，其中 $K$ 表示集成模型的数量，$l_k(x)$ 是第 $k$ 个模型的输出 logits，$w_k$ 是第 $k$ 个模型的集成权重且 $w_k>0({\sum }_{k=1}^K{w}_k=1)$，在无特殊说明时，文中使用的融合 logits 为这些模型的平均值。

• 通过采用 Poincaré 度量，使得梯度幅值在且仅在数据点靠近目标标签（即靠近表面）时增长，从而实现了梯度的自适应调整，让噪声的方向变得更加灵活，有助于提升目标攻击的效果和对抗样本的可迁移性。

用于目标攻击的三元组损失-Triplet Loss for Targeted Attack

该部分主要介绍了针对目标攻击引入的三元组损失（Triplet Loss）。

• 在目标攻击中，传统损失函数通常仅与目标标签相关，这导致生成的对抗样本可能与原始类过于接近，使得部分对抗样本仍被目标模型分类到原始类。为解决此问题，引入了度量学习中的经典三元组损失到目标攻击过程。

• 三元组损失不仅能减小对抗样本输出与目标标签的距离，还能增大其与真实标签的距离。其典型形式为 ${\mathcal{L}}_{trip}(x^a,x^p,x^n)=[D(x^a,x^p)-D(x^a,x^n)+\gamma {]}_{+}$，其中 $\gamma \ge 0$ 是定义距离度量 $D(x^a,x^p)$ 和 $D(x^a,x^n)$ 之间间隔的超参数，$x^a$、$x^p$、$x^n$ 分别代表锚点、正例和负例。

• 但在目标攻击场景下，难以像标准情况那样从原始数据集采样三元组输入，因为通常只有少量图像而非整个数据集。因此，文中决定使用干净图像的 logits $l(x_{clean})$、one - hot 目标标签和真实标签 $y_{tar}$、$y_{true}$ 作为三元组输入，即 ${\mathcal{L}}_{trip}(y_{tar},l(x_i),y_{true})=[D(l(x_i),y_{tar})-D(l(x_i),y_{true})+\gamma {]}_{+}$.

• 又因为 $l(x^{adv})$ 未归一化，所以采用角距离作为距离度量 $D(l(x^{adv}),y_{tar})=1-\frac{|l(x^{adv})\cdot y_{tar}|}{\Vert l(x^{adv}){\Vert }_2\Vert y_{tar}{\Vert }_2}$，角距离可排除范数对损失值的影响。

• 最后，将三元组损失项添加到损失函数中，得到总体损失函数 ${\mathcal{L}}_{all}={\mathcal{L}}_{Po}(l(x),y_{tar})+\lambda \cdot {\mathcal{L}}_{trip}(y_{tar},l(x_i),y_{true})$，以此来提高生成的对抗样本的可迁移性，并使对抗样本远离真实类。

---

实验-Experiments

该部分通过一系列实验评估所提方法性能，并与其他先进对抗方法在大规模 ImageNet 数据集上进行对比。

• 实验设置

  • 数据集：采用包含 1000 张图像的 ImageNet 兼容数据集开展实验。
  • 网络：研究 9 种 ImageNet 上的先进网络，包括 6 种正常训练模型（如 Inception - v3、Inception - v4 等）和 3 种对抗训练模型（如 ens3 - advInception - v3 等）。
  • 参数：各攻击者参数遵循已有研究默认设置，如步长 $\alpha =ϵ/T$、迭代次数 $N=20$、最大像素扰动 $ϵ=16$ 等，同时设定了动量项衰减因子、随机输入多样性概率等，在本文方法中还确定了三元组损失权重 $\lambda =0.01$ 和 margin $\gamma =0.007$。
  • 攻击方法：选用 $D{I}^2-FGSM$ 和 TI - FGSM 两种先进的基于迭代的黑盒攻击方法作对比，同时在补充材料中展示了 MI - FGSM 等更多方法的实验结果。
    

• 攻击自然训练模型结果：对抗样本在白盒和黑盒攻击不同设置下进行测试。白盒攻击中，所提方法平均比 $D{I}^2-FGSM$ 和 TI - FGSM 成功率高 7.0%和 5.9%；黑盒攻击时，比这两种方法成功率高出 8%以上，且生成的对抗样本与干净图像差异微小，人眼难以察觉。
  
  表 1：与 $D{I}^2-FGSM$ 和 TI - FGSM 相比的有目标性对抗攻击的成功率（%）。其中“-”、“Po”和“Trip”分别表示留出网络、庞加莱距离和三元组损失。有目标性的对抗样本是在一组网络上生成的。结果表明，该方法在集成网络（白盒设置）和留出网络（黑盒设置）中均显著优于其他所有方法。
  
  图 5：我们生成的 $ϵ=16$ 的对抗样本（第一行）及其对应的原始图像（第二行）和添加的噪声（第三行）。可以看出几乎没有明显差异。这些图展示的是数据集中的前 5 张图像。

• 攻击对抗训练模型结果：对抗训练模型对对抗样本有更强抗性，但本文方法仍表现更优，证明了其在应对更具挑战性的对抗训练模型时生成可迁移对抗样本的有效性，突破了现有方法的局限。
  
  表 2：与针对一组白盒模型和一个留出的黑盒目标模型的 $D{I}^2-FGSM$ 和 TI - FGSM 相比，有目标性的对抗攻击在对抗训练模型上的成功率（%）

• 消融研究

  • Poincaré 度量影响：对比基于交叉熵损失和 Poincaré 距离的方法，实验表明随着迭代，前者梯度下降，后者梯度适度增长，使更新方向更聚焦当前梯度，避免噪声固化，从而使对抗样本更新方向更优。
    
    图 6：迭代过程中的梯度值。为避免选择性挑选数据，结果是在具有 1000 个样本的公共 ImageNet 兼容数据集的前 10 张图像上取平均值得到的。
  • 三元组损失影响：将对抗样本分为目标转移成功、非目标转移成功和正确分类三类。结果显示 Poincaré 攻击虽能找到有效噪声方向，但会使部分样本被正确分类，而三元组损失可使对抗样本远离真实类，增强迁移性，弥补了 Poincaré 攻击的不足。
    
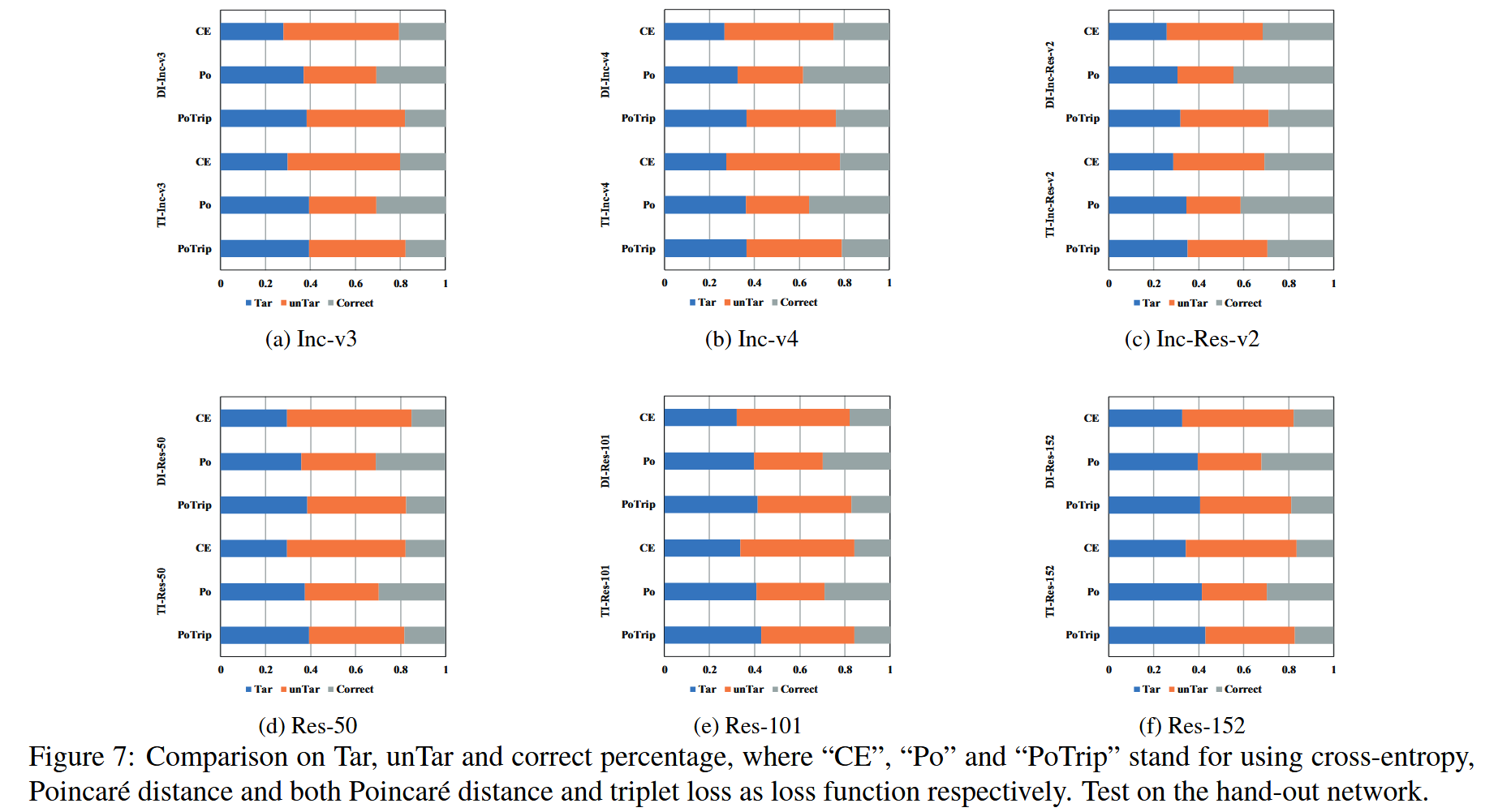
    图 7：对目标转移成功样本（Tar）、非目标转移成功样本（unTar）和正确分类样本（correct）百分比的比较，其中“CE” “Po” 和 “PoTrip” 分别代表使用交叉熵、庞加莱距离以及庞加莱距离和三元组损失作为损失函数。在留出网络上进行测试。

---

结论-Conclusion

本文摒弃了将目标攻击视为非目标攻击简单延伸的传统观点，而是基于在目标攻击中发现的特殊性质开展研究。通过利用 Poincaré 距离和三元组损失，成功提出了一种全新的可迁移目标攻击方法。

该方法借助高容量的 Poincaré 空间作为度量空间，有效避免了噪声固化问题，同时基于度量学习的方式充分挖掘了额外的真实标签信息。

在 ImageNet 数据集上进行的大量实验结果充分表明，与传统攻击方法相比，新提出的攻击方法在目标攻击场景下，无论是针对黑盒模型还是白盒模型，都取得了显著更高的攻击成功率，有力地证明了该方法在提升对抗样本迁移性方面的有效性和优越性，为后续相关领域的研究提供了重要的参考和借鉴。