【FOC磁场定向控制】自制FOC驱动器

---

引言

  无刷直流电机（Brushless Direct Current Motor, BLDCM）矢量控制（Field-Oriented Control, FOC）技术历经数十年发展已日趋成熟，其应用场景已深度渗透至民生领域与工业体系。在日常生活场景中，该技术广泛赋能新能源汽车驱动系统、滚筒洗衣机变频模块、真空吸尘器动力单元、扫地机器人行走机构及智能电风扇调速系统等终端产品；在工业与特种领域，其更是工业机器人高精度伺服关节、军用无人机动力系统等核心装备实现稳定运行的关键支撑技术。可以说，在依赖电机驱动的现代化装备体系中，矢量控制技术已成为保障其性能的核心基础技术之一。
  相较于传统方波控制策略，矢量控制技术通过磁场与转矩的解耦控制，可显著降低电机运行过程中的转矩脉动，进而满足装备对高精度定位、快速动态响应及平稳运行的严苛需求。近年来，伴随全球机器人产业的爆发式增长，对电机驱动系统的控制精度、动态性能及可靠性提出了更高要求，使得矢量控制技术的学术研究价值与工程应用价值进一步凸显，成为相关领域的研究热点之一。

---

一、无刷电机的概念与控制原理

1.1 概念

  直流无刷电机的驱动，就是依靠改变电机定子线圈的电流交变频率和波形，在定子周围形成磁场，驱动转子永磁体转动，进而带动电机转起来。因此，研究如何产生和改变输入定子三相的电流交变频率和波形是我们的工作重点。

1.2 六步换相法

  一对极电机的霍尔传感器安装位置如图1.2所示。每个电机只需要3个霍尔传感器，并呈120°电角度摆放，就能准确检测定子三相的换向时刻。也有按60°电角度摆放的，只是霍尔传感器输出顺序不同，原理上一样。

1.2 一对极电机的霍尔传感器安装位置

  每当霍尔传感器经过磁极时，其输出状态便改变一次。这样，磁场旋转一个电周期，每个霍尔传感器会改变2次输出状态，3个霍尔传感器共改变6次输出状态，这便是六步换相法原理。
  电角度指的是磁场旋转角度：机械角度×极对数=电角度；电周期指的是磁场旋转的周期。

1.3 三相全桥逆变电路

  如图1.3所示，假设某一时刻，与$A$相连接的两个功率管$Q_1$和$Q_2$关断，电机的$A$相浮空；与$B$相连接的上桥臂功率管$Q_3$开通，B相连接到电源的正极。为了防止短路，上下两个功率管不能同时开通，因此$Q_3$开通的时候，$Q_4$必须关断。与$C$相连接的上桥臂功率管$Q_5$关断，下桥臂功率管$Q_6$开通，$C$相直接与电源的负极连接。此时，电流从电源的正极进入$Q_3$，流入电机的$B$相，并从电机的$C$相流出，最后通过$C$相的下桥臂功率管$Q_6$进入电源的负极。

1.3 电机逆变器驱动电路

  通电线圈产生磁场，在定子磁场的作用下会产生一定角度的旋转。如果这个时候根据霍尔传感器的输出状态，改变功率管的开通顺序，转子会持续转动到下一个位置。根据霍尔传感器的输出状态，那么转子会不停地从一个位置运动到另一个位置，从而周期性地旋转起来。每一次改变通电顺序，称为一次换向，一个电周期共需要6次换向，这就是所谓的六步换向。旋转时，定子磁场和转子磁场始终保持适当的角度差，要使电机产生的力矩增大，可以适当调整定子磁场领先转子磁场的角度。

二、矢量控制

2.1 Clarke变换

  Clarke变换实际上就是降维解耦的过程，把难以辨别和控制的三相相位差，120°的电机波形降解为二维矢量。如图2.1所示为Clarke变换：

2.1 Clarke变换

  由图2.1可推导公式如式$(1)、(2)、(3)$所示：
针对$\alpha -\beta$坐标系中的 $\alpha$ 轴：
$$\{\begin{array}{l}{I}_{\alpha }=i_a-\sin 30^{\circ }{i}_b-\cos 60^{\circ }{i}_c\\ I_{\alpha }=i_a-\frac{1}{2}{i}_b-\frac{1}{2}{i}_c\end{array}\text{\hspace{1em}(1)}$$
针对$\alpha -\beta$坐标系中的 $\beta$ 轴：
$$\{\begin{array}{l}{I}_{\beta }=\cos 30^{\circ }{i}_b-\cos 30^{\circ }{i}_c\\ I_{\beta }=\frac{\sqrt{3}}{2}{i}_b-\frac{\sqrt{3}}{2}{i}_c\end{array}\text{\hspace{1em}(2)}$$
  将公式$(1)、(2)$写成矩阵形式，得Clarke变换基本形式，如式$(3)$所示：
$$\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]\text{\hspace{1em}(3)}$$
  等幅值Clarke变换形式，如式$(4)$所示：
$$\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]\text{\hspace{1em}(4)}$$
  等功率Clarke变换形式，如式$(5)$所示：
$$\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\sqrt{\frac{2}{3}}\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]\text{\hspace{1em}(5)}$$
式$(4)$为Clarke等幅值正变换，是将三相相位差降解为二维矢量，为了控制三相相位输出，因此需要采用Clarke逆变换，得Clarke等幅值逆变换，如式$(6)$所示：
$$\{\begin{array}{l}{i}_a=I_a\\ i_b=\frac{\sqrt{3}{I}_{\beta }-I_a}{2}\\ i_c=\frac{-I_a-\sqrt{3}{I}_{\beta }}{2}\end{array}\text{\hspace{1em}(6)}$$

2.2 Park变换

  通过 2.1 节阐述的克拉克变换（Clarke Transformation），可有效对无刷电机正弦驱动模式下的三相电流曲线实施降维处理，将其从三相静止坐标系问题转化为 $\alpha -\beta$ 两轴静止坐标系问题；与此同时，该变换的正变换与逆变换关系亦已通过推导得以明确。
  但是只有它是不够的，还需要将这个理论和旋转的电机对应起来，也就是建立电机在旋转时候的数学模型，可以得到 $I_{\alpha }$ 和 $I_{\beta }$，从而控制三相输出；而Park变换正是一种能够把电机旋转的物理状态转化为变化的 $I_{\alpha }$ 和 $I_{\beta }$ 的一种数学转换方法。如图2.2所示为Park变换：

2.2 Park变换

  由图2.2可知，$\alpha -\beta$坐标系是固定在电机定子上的；$d-q$坐标系是可以随电机转动而转动的，以电机的转子固连。图2.2中，$d-q$坐标系因转动而造成与$\alpha -\beta$坐标系的差角$\theta$，就被称为电角度。
  由图2.2可推导公式如式$(7)、(8)、(9)$所示：
对于映射到$D$轴上的$\alpha ，\beta$分量：
$$i_d=i_{\alpha }\cos \theta +i_{\beta }\sin \theta \text{\hspace{1em}(7)}$$
对于映射到$Q$轴上的$\alpha ，\beta$分量：
$$i_q=-i_{\alpha }\sin \theta +i_{\beta }\cos \theta \text{\hspace{1em}(8)}$$
  将公式$(7)、(8)$写成矩阵形式，得Park变换基本形式，如式$(9)$所示：
$$\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]\text{\hspace{1em}(9)}$$
  式$(9)$所示的矩阵被称为旋转矩阵，亦是Park正变换；则对式$(9)$矩阵取逆，进行逆变换并拆分得到，如式$(10)$所示：
$$\{\begin{array}{l}{i}_{\alpha }=i_d\cos \theta -i_q\sin \theta \\ i_{\beta }=i_q\cos \theta +i_d\sin \theta \end{array}\text{\hspace{1em}(10)}$$
  由式$(10)$可知，通过设定$i_q$与$i_d$的给定值即可表征电机的旋转状态；当驱动电机运行时，系统将持续生成新的电角度，进而循环输出控制指令以维持电机的旋转过程。通常在简单的foc控制中，只需要控制$i_q$的大小，而把$i_d$设置为零；此时$i_q$的大小间接就决定了定子三相电流的大小，进而决定了定子产生磁场的强度，再进一步可以说明$i_q$决定了电机产生力矩大小；只要电机能够产生力矩，那么电机就会绕着它的中轴旋转，从而改变电角度产生新的电角度，通过新电角度变换后产生正确的力矩以维持电机旋转过程。

三、SVPWM

  由第二章节所述的spwm方法相比于svpwm的效率(电压利用率)会低1.1547倍，为了解决这个损失从而提升效率，产生了svpwm；svpwm数学方法的产生，正是为了解决spwm算法效率低的问题，换来的就是电机力矩的提升，以及更好的电机运动效果。
  所以，从spwm改进到svpwm的方法就是，在spwm波形上叠加锯齿波以达到削峰效果，即可得马鞍波。

3.1 合成矢量

  实际上，svpwm的公式就是用电机的六步换相法来进行描述的；详细请见1.2小节。若以六步换相法建立矢量关系，那么每换向一步电机就要前进60°，即分辨率为60°，这种情况过于粗糙。那么如何优化六步换相法使电机控制变得连续呢？即引出svpwm算法的第一步：通过矢量合成360°范围内的各个磁场。

3.2 扇区

  由1.3小节可知，定义：上面3颗mos管为上桥臂，下面3颗mos管为下桥臂。假定上桥臂开通，下桥臂关断，将该桥臂的状态记为1，反之记为0。因为有3个桥臂，因此我们可以定义开关函数$S_x$（$x=a,b,c$）为：
$$S_x=\{\begin{array}{ll}1& \text{上桥臂开通，下桥臂关断}\\ 0& \text{上桥臂关断，下桥臂开通}\end{array}\text{\hspace{1em}(11)}$$
  于是，3个桥臂的状态可以有$2^3=8$种，也就是A、B、C三相共有8种状态组合。
  假设一种状态组合为A相上桥臂开通，下桥臂关断，A相直接连接到电源的正极；B相上桥臂关断，下桥臂开通，B相直接连接到电源的负极；C相上桥臂关断，下桥臂开通，C相直接连接到电源的负极。也就是说$S_{\text{a}}=1$、$S_{\text{b}}=0$、$S_{\text{c}}=0$，此时的等效电路如图3.2a所示。

3.2a 状态100时的等效电路

  我们用$U_{\text{a}}$、$U_{\text{b}}$、$U_{\text{c}}$表示各相的相电压，也就是各相相对于电机中性点$\text{N}$的电压：
$$\{\begin{array}{l}{U}_{\text{a}}=U_{\text{A}}-U_{\text{N}}\\ U_{\text{b}}=U_{\text{B}}-U_{\text{N}}\\ U_{\text{c}}=U_{\text{C}}-U_{\text{N}}\end{array}\text{\hspace{1em}(12)}$$
  那么在$S_x$（$x=a,b,c$）的状态为100时，B相与C相相当于并联后再与A相串联，由图4.2所示的等效电路可以推出：
$$\{\begin{array}{l}{U}_{\text{a}}=\frac{2}{3}{U}_{\text{dc}}\\ U_{\text{b}}=-\frac{1}{3}{U}_{\text{dc}}\\ U_{\text{c}}=-\frac{1}{3}{U}_{\text{dc}}\end{array}\text{\hspace{1em}(13)}$$
  将8个矢量放到矢量分布图中，如图3.2b所示，红色为A-B-C三相空间静止坐标系。$U_0(100)$表示A相上桥臂开通，A相直接连接到电源的正极；B相和C相下桥臂开通，B相和C相直接连接到电源的负极。此时起作用的是A相，因此该矢量与A轴重合，$U_0(100)$中的下标“0”表示其在矢量圆中的位置为$0^{\circ }$。

3.2b 基础矢量与矢量圆

  $U_{120}(010)$表示B相上桥臂开通，B相直接连接到电源的正极；A相和C相下桥臂开通，A相和C相直接与电源的负极连接。此时起作用的是B相，因此该矢量与B轴重合，所以在空间上与$U_0(100)$相差$120^{\circ }$，下标“120”表示其在矢量圆中的位置为$120^{\circ }$。
  其他矢量以此类推，黑色的中间矢量$U_{60}(110)$可以看作相邻矢量$U_0(100)$和$U_{120}(010)$的合成矢量；$U_{\text{z}}(111)$和$U_{\text{z}}(000)$是零矢量，它们不产生磁场，对电机不起作用。
  根据伏秒平衡原理，一个开关周期内某个矢量的作用效果等同于与它相邻的两个基础矢量分别作用不同时间的效果之和。
  假定某个非零矢量$U_{\text{ref}}$位于图3.2b所示矢量图的扇区Ⅰ中，那么如图3.2c所示，$T_4$是基础矢量$U_0(100)$的作用时间，$T_6$是基础矢量$U_{60}(110)$的作用时间。

3.2c 扇区Ⅰ的基础矢量合成

  二进制数100代表十进制数4，二进制数110代表十进制数6。为了区分各个基础矢量的作用时间，我们以6个基础矢量的二进制开关函数表示基础矢量的作用时间。

3.3 矢量作用时间与七段式调制方式分析

  通过图3.2c可知，使用六步换相法的基础矢量合成任意位置的矢量。
V4矢量的通电做功时间 T1:
$$T_1=T\times DC\times \sin (60°-\alpha )\text{\hspace{1em}(14)}$$
V6矢量的通电做功时间 T2:
$$T_2=T\times DC\times \sin (\alpha )\text{\hspace{1em}(15)}$$
不做功的时间：
$$T_0=1-T_1-T_2\text{\hspace{1em}(16)}$$
  T是控制周期的长短，对于单位周期，我们可以直接设置T=1
  DC与前面提到的Iq/Uq相关，可以理解为想要产生的磁场强度
由于V4和V6的做功都在同一个周期内发生的，因此，相同相的做功时间其实可以叠加，如：
  对于V4矢量来说，要合成DC，三相做功时间是：
$$T_1\times (1,0,0)=(T1,0,0)\text{\hspace{1em}(17)}$$
  对于V6矢量来说，要合成DC，三相做功时间是：
$$T_2\times (1,1,0)=(T2,T2,0)\text{\hspace{1em}(18)}$$
  叠加式$(17)、(18)$做功时间，有：
$$(T1,0,0)+(T2,T2,0)=(T1+T2,T2,0)\text{\hspace{1em}(19)}$$
  则有：
$$\{\begin{array}{l}{T}_a=T_1+T_2\\ T_b=T_2\\ T_c=0\end{array}\text{\hspace{1em}(20)}$$
  然而，对于svpwm，三相pwm占空比采用中间调制的方式，如图3.3所示：

3.3 七段式调制的扇区波形

  因此，对式$(20)$转化得：
$$\{\begin{array}{l}{T}_a=T_1+T_2+\frac{T_0}{2}\\ T_b=T_2+\frac{T_0}{2}\\ T_c=0+\frac{T_0}{2}\end{array}\text{\hspace{1em}(21)}$$

3.4 Uq与T1，T2的关系

  经过上述章节内容讲解与推导得最终关系为：
$$\begin{array}{rl}& \sqrt{U_{\alpha }^2+U_{\beta }^2}=\frac{2}{3}\sqrt{u_a^2+u_b^2+u_c^2}\\ & \sqrt{(u_a+u_b+u_c{)}^2}=|u_a{|}^2+|u_b{|}^2+|u_c{|}^2+2|u_a||u_b|\cos (60^{\circ })+2|u_a||u_c|\cos (60^{\circ })+2|u_b||u_c|\cos (120^{\circ })=U_{dc}=|DC|\\ & \sqrt{U_{\alpha }^2+U_{\beta }^2}=\frac{2}{3}|DC|\\ & T_1=\frac{2\sqrt{3}}{3}\frac{|DC|}{U_{dc}}{T}_s\sin (60^{\circ }-\alpha )=\sqrt{3}\frac{\sqrt{U_{\alpha }^2+U_{\beta }^2}}{U_{dc}}{T}_s\sin (60^{\circ }-\alpha )=\sqrt{3}\frac{\sqrt{U_q^2+U_d^2}}{U_{dc}}{T}_s\sin (60^{\circ }-\alpha )\\ & T_2=\frac{2\sqrt{3}}{3}\frac{|DC|}{U_{dc}}{T}_s\sin (\alpha )=\sqrt{3}\frac{\sqrt{U_{\alpha }^2+U_{\beta }^2}}{U_{dc}}{T}_s\sin (\alpha )=\sqrt{3}\frac{\sqrt{U_q^2+U_d^2}}{U_{dc}}{T}_s\sin (\alpha )\end{array}\text{\hspace{1em}(22)}$$

四、有感FOC

  有感控制又名有传感器FOC控制，指的就是利用电机上的物理角度传感器，来准确地测得转子的位置，即：电角度。例如，使用AS5600编码器。

五、无感FOC

  无感FOC是利用其他的方法来估计这个转子的位置，即：电角度。
方法：从电机的相电流进行间接推算而得到；利用"反电动势"估算电机转子位置，如式$(23)$所示：
$$\frac{di}{dt}=-\frac{R_m}{L_m}{I}_m+\frac{1}{L_m}(U_a-V_{BEMF})\text{\hspace{1em}(23)}$$
  式$(23)$所示为重要推论：电机的电压方程，此方程是针对a，b，c相的等效电路提出的。
方法：利用$U_{\alpha }$，$U_{\beta }$，$i_{\alpha }$，$i_{\beta }$推算出$V_{BEM{F}_a}$，$V_{BEM{F}_b}$的方法，如式$(24)$所示：
$$\theta =-\arctan \left(\frac{V_{BEMF\_a}}{V_{BEMF\_\beta }}\right)\text{\hspace{1em}(24)}$$
  式$(24)$所示为重要推论：反正切求解电角度，此方程是针对$\alpha -\beta$轴上的反电动势提出的。

5.1 滑膜观测器

  为什么要使用滑膜观测器呢，看式$(25)$所示：
$$V_{BEMF\_a}=-\left(\frac{L_m}{T_s}\right)(i_{a\_now}-i_{a\_prev})+R_m{i}_{\alpha \_now}-U_{\alpha }\text{\hspace{1em}(25)}$$
  由于不同负载情况下，线圈不同的发热情况会带来电阻和电感量，磁导率的变化；如果直接计算$V_{BEMF\_a}$会造成信号毛刺超大无法使用。
因此，使用不同的估测值去计算一个可稳定测量的值进行不断矫正估测的$V_{BEMF\_a}$，这种逆向递推跟随思路，即：滑膜观测器，如式$(26)$所示：
$$i_{a\_now}(\text{预测})=i_{a\_prev}+T_s\left[-\frac{R_m}{L_m}{i}_{a\_now}+\frac{1}{L_m}(U_a-V_{BEMF\_a})\right]\text{\hspace{1em}(26)}$$饱和函数sat:
$$V_{BEMF\_a}=h\times \text{sat}(i_{a\_now}(\text{预测})-i_{a\_now})\text{\hspace{1em}(27)}$$
  由于滑膜观测器观测对象实际上是反电动势，因此在静止状态下不适用，如果在静止时也能产生反电势的话，就要借助高频注入的概念了。

5.2 PLL锁相环

  如图5.2所示为无感PLL观测器示意图。

5.2 无感PLL观测器示意图

  由式$(9)$推导得反电动势的帕克逆变换，如式$(28)$所示：
$$\left[\begin{array}{c}{E}_d\\ E_q\end{array}\right]=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}{E}_{\alpha }\\ E_{\beta }\end{array}\right]\text{\hspace{1em}(28)}$$
  从式$(28)$中分离出$d$分量：
$$E_d=E_{\alpha }\cos \theta +E_{\beta }\sin \theta \text{\hspace{1em}(29)}$$
  将条件1：$I_d=0$的工况下$E_d=0$的工况代入式$(29)$得：
$$E_d=E_{\alpha }\cos \theta +E_{\beta }\sin \theta =0\text{\hspace{1em}(30)}$$
  $\theta$为电角度，若条件1成立的情况下，如果算法观测电角度$\theta$与电机运行状态匹配$E_d$就一定为0。PLL锁相环正是利用了$I_d$等于0时，$E_d$等于0这一点的物理特性，来实现无感电角度观测功能的，如式$(31)$所示：
$$E_{dest}=E_{\alpha }\cos {\theta }_{est}+E_{\beta }\sin {\theta }_{est}=0\text{\hspace{1em}(31)}$$
  将式$(30)$中的$\theta$替换成了无感算法中估计的电角度${\theta }_{est}$，式中，$E_{dest}$是根据PLL算法观测的电角度${\theta }_{est}$求得的$d$轴反电动势。
$$E_{dest}=E_{\alpha }\cos {\theta }_{est}+E_{\beta }\sin {\theta }_{est}\ne 0\text{\hspace{1em}(32)}$$
  如果${\theta }_{est}$不准确，则会变成公式$(32)$。
则，可以误差使用式$(33)$表示：
$$error=E_d-E_{dest}\text{\hspace{1em}(33)}$$
由于实际物理系统中$E_d=0$，展开式子，得到：
$$error=E_d-E_{dest}=0-\left(E_{\alpha }\cos {\theta }_{est}+E_{\beta }\sin {\theta }_{est}\right)\text{\hspace{1em}(34)}$$
  而PLL的原理，就是利用公式$(34)$这个真实的$d$轴反电动势$E_d$和由${\theta }_{est}$预测的电机反电动势$E_{dest}$的差值$error$，来估算转子的角速度$\theta$点。
式$(35)、(36)$就是PLL算法的速度估计式：
$$i_{err}=\sum T_s\times K_i\times error\text{\hspace{1em}(35)}$$
  式(35)中的$K_i$转换系数，一般根据实际无感闭环效果调试得出。
$$\dot{\theta }=K_p\times error+i_{err}\text{\hspace{1em}(36)}$$
  式$(36)$是无感FOC PLL法电机转子角速度估计式。
构建低通滤波，获取低通滤波速度：
$$\dot{{\theta }_{fil{t}_{now}}}=\dot{{\theta }_{fil{t}_{prev}}}\times 0.9+\dot{\theta }\times 0.1\text{\hspace{1em}(37)}$$
无感FOC PLL法电机转子电角度估计式：
$${\theta }_{est}=\sum T_s\times \dot{{\theta }_{fil{t}_{now}}}\text{\hspace{1em}(38)}$$
5.2小节公式描述均可反扑图5.2与之对应。

5.3 PLL观测器与滑膜观测器的性能区别

滑膜观测器：
$${\theta }_{est}=-\arctan \left(\frac{V_{BEMF\_a}}{V_{BEMF\_\beta }}\right)\text{\hspace{1em}(39)}$$
  ${\theta }_{est}$微分后为$\dot{\theta }$。特点：通过对反电动势这个含毛刺量反正切得到电角度${\theta }_{est}$，再微分得到电角度$\dot{\theta }$；直接处理毛刺量，导致信号毛刺大，不干净。
PLL观测器：
$$\dot{\theta }=K_p\times error+i_{err}\text{\hspace{1em}(40)}$$
  $\dot{\theta }$积分后为${\theta }_{est}$。特点：通过对电机运动物理原理的理解先把$error$类推为角度加速度，再积分求角速度$\dot{\theta }$；最后积分求的电角度${\theta }_{est}$不直接处理毛刺量，信号更纯净。

5.4 VF算法

  VF启动(Voltage-Frequency，电压-频率比 开环启动)。无感FOC启动流程思路，先通过VF算法开环启动产生足够的反电动势，以供观测器观测后，再到观测器代替编码器，观测速度和电角度的闭环模式。

六、硬件电路搭建

6.1 主控电路与通信电路设计

  在构建本文所述系统架构时，单片机最小系统作为维持系统正常运行的基础单元，为整个系统的稳定工作提供了底层支撑 ，如图6.1所示为STM32最小系统框图。

6.1 STM32最小系统与通信电路图

  由图3.1可以看出STM32最小系统的硬件组成部分主要有:微控制器MCU、电源电路、晶振电路、复位电路等。电源电路通过线性稳压器AMS1117将输入4.75V至15的电压降为最小系统所需的3.3V稳定电压。晶振电路为系统提供了稳定和精确的时钟频率,同时外接与晶振频率相匹配的负载电容。复位电路包括一个复位按钮,连接到STM32F1芯片上的NRST引脚以允许手动复位,复位引脚还需要一个上拉电阻以确保在没有按下复位按钮时,引脚保持高电平状态。这些电路的设计共同构建了一个STM32最小系统。
  为提升系统通信兼容性与供电适配性，设计中额外集成CAN通信接口，以满足不同场景下多设备间的数据交互需求。

6.2 三相全桥逆变电路设计

  在永磁同步电机FOC控制系统中，三相逆变电路是不可或缺的“能量转换核心”——它将直流母线电压通过PWM调制逆变为三相可调交流电压，精准驱动电机定子绕组，同时为FOC算法的电流闭环、磁链定向提供物理执行载体。其经典三相全桥拓扑（6个功率开关器件构成），配合SVPWM等策略，既能最大化利用母线电压、降低电流谐波，又需通过死区补偿、散热设计与故障保护，平衡控制精度与运行可靠性，是FOC技术从理论落地工程的关键环节，如图6.2所示。

6.2 三相全桥逆变电路设计

6.3 PCB板的设计与开发

6.3.1 系统原理图设计

  为了更好的实现本文系统的实物展示，本文采用嘉立创EDA软件进行系统原理图绘制，如图6.3.1所示为系统原理图。

6.3.1 系统原理图

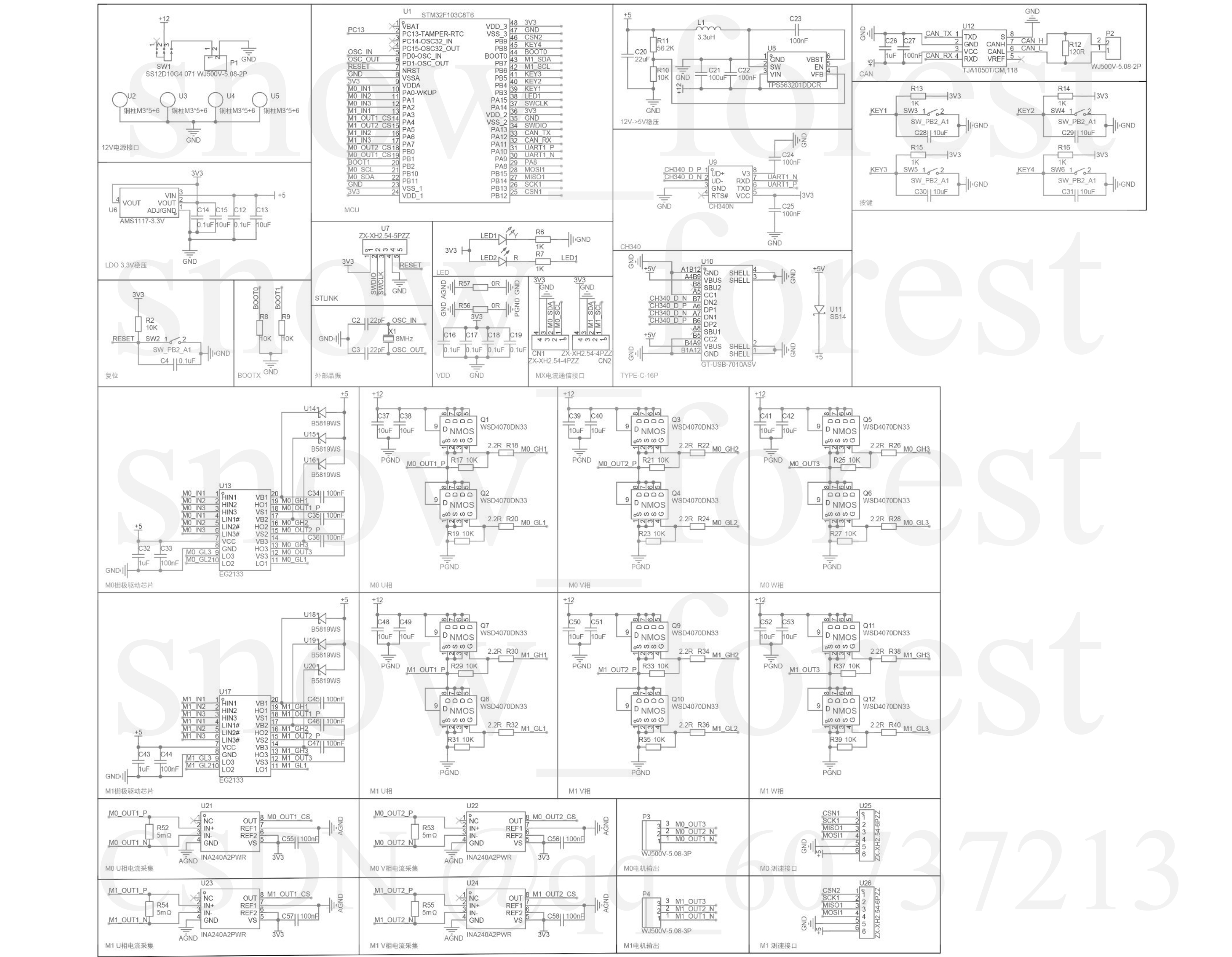
6.3.2 系统PCB布局布线

  通过原理图的绘制，然后转到PCB板的绘制，从布局和布线去减少器件间的耦合性等干扰特性，如图6.3.2所示为系统PCB。

6.3.2 系统PCB

总结

  本文围绕无刷直流电机矢量控制（FOC）技术展开系统研究，先阐述了无刷电机的驱动本质、六步换相法及三相全桥逆变电路等基础原理；随后深入推导了FOC核心的Clarke变换与Park变换，并分析了SVPWM技术的矢量合成、扇区划分及作用时间计算等优化策略，以提升电压利用率与电机性能；还对比了有感FOC与无感FOC的实现方式与性能差异；最后介绍了基于STM32的主控、通信及三相全桥逆变电路设计与PCB开发流程，形成了从理论算法到硬件实现的完整技术框架。

参考资料

【自制FOC驱动器】深入浅出讲解FOC算法与SVPWM技术
FOC学习笔记-基于灯哥FOC
一套极简易的直流无刷电机(Deng FOC)开发套件介绍
SimpleFOC（Dengfoc）移植STM32F407HAL库(一 )-----开环控制