怎么算两列数之间的 correlatoin coefficient?
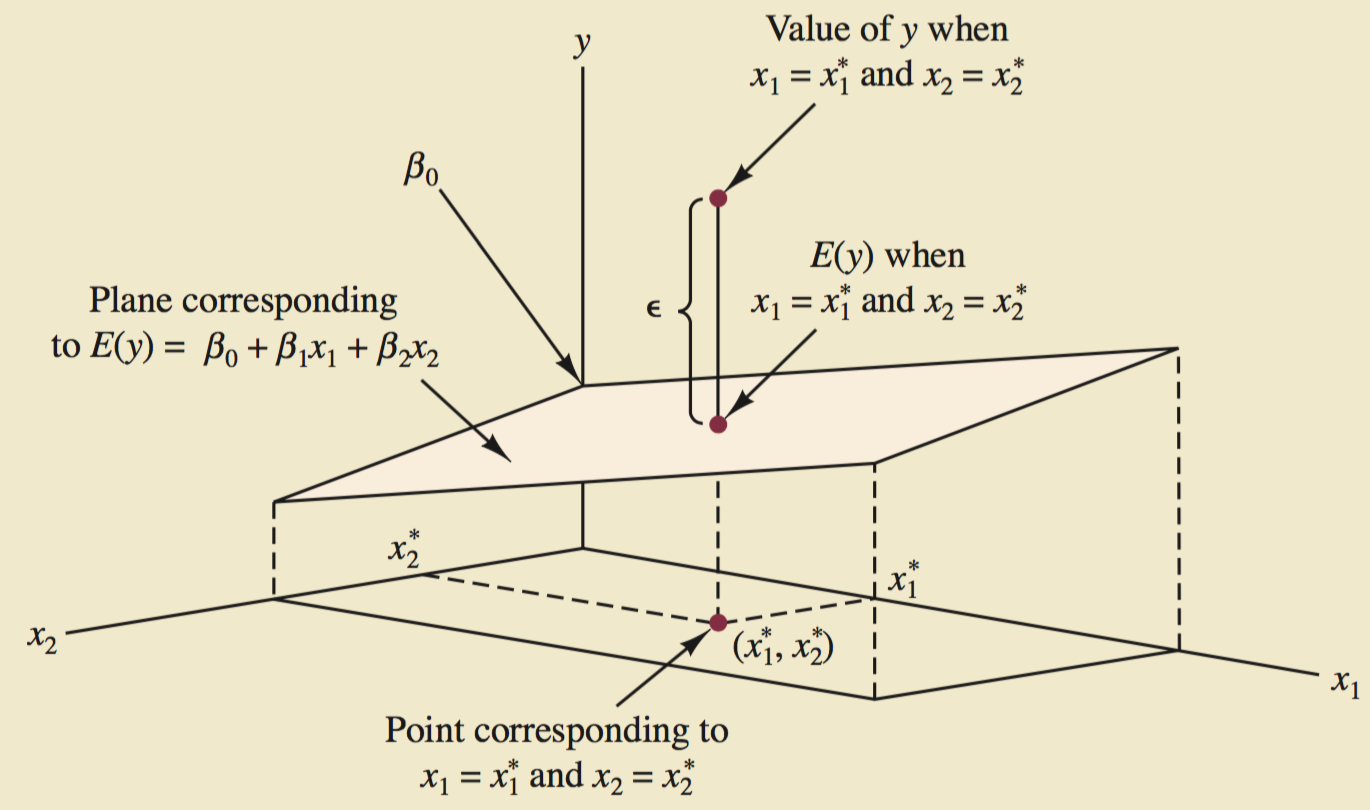
15.1 Multiple Regression Model
15.3 Coefficient of Determination
Why Adjusted?
Avoid overestimating the impact of adding an independent variable on the amount of variability explained by the estimated regression equation.
15.4 Model Assumptions
15.5 Testing for Significance
F test for overall significance; T test for individual significance
F Test
H0: β1 = β2 = … = βp = 0
Ha: One or more of the parameters is not equal to zero

n= 观测数目
p =自变量数目
t Test
Multicollinearity 多重共线性
当多元回归方程总体显著性的 F 检验表明有一个显著关系时,我们可能得出单个参数没有一个是显著地不同于0的结论。只有当自变量之间的相关性非常小,才有可能回避这个问题。
F test is significant. but two t test is not significant. With x2 already in the model, x1 does not make a significant contribution to determining the value of y. 怎么发现?当两个自变量的 correlation coefficient >0.7
15.7 Qualitative Independent Variables
如果 qualitative variables 是两个的话,那么可以变成 0 1
The important point to remember is that when a qualitative variable has k levels, k-1 dummy variables are required in the multiple regression analysis.
15.8 Residual Analysis
Detecting Outliers
Minitab classifies an observation as an outlier if the value of its standardized residual is less than -2 or greater than +2.
Influential Observations
Minitab computes the leverage values and uses the rule of thumb hi > 3( p + 1)/n to identify influential observations.
Cook’s Distance
如果 Di >1,那么表明第 i 次观测值是一个有影响力的观测值,并对这个观测值做进一步的考察。
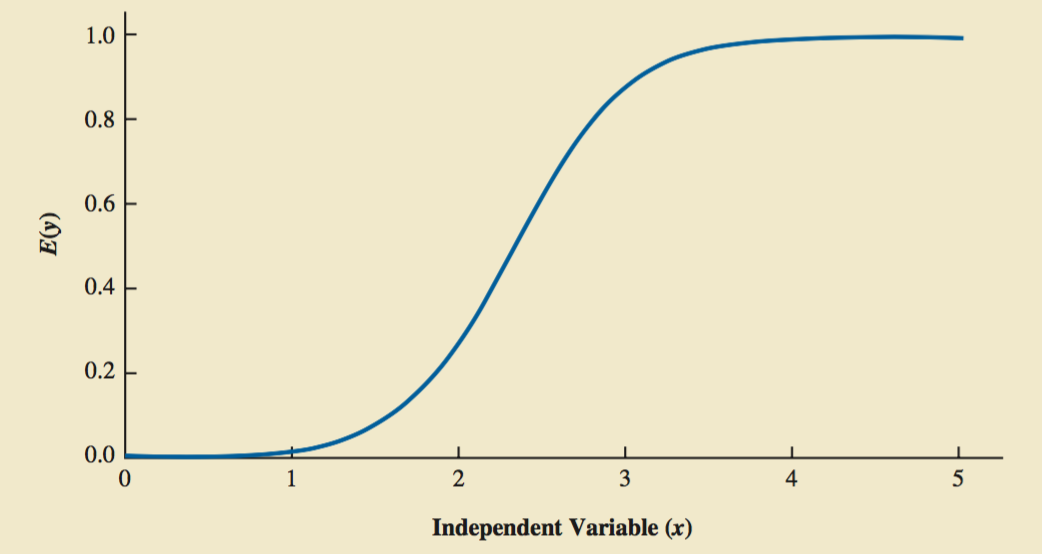
15.9 Logistic Regression

The Probability of y=1 given x1,x2,…,xp
Testing for Significance
H0: β1 = β2 = 0
Ha: One or both of the parameters is not equal to zero
G follows a chi-square distribution with degrees of freedom equal to the number of independent variables in the model
如果是一个个的 Variable,就用 z test
Managerial Use
问题是:发 coupon,想预测一下哪些消费者在收到 coupon 会用?
通过 logistics regression,得到下面的这张表:

结果:
Customers who have a Simmons credit card: Send the catalog to every customer who spent 2000 or more last year
Customers who do not have a Simmons credit card: Send the catalog to every customer who spent 6000 or more last year
Interpreting Logistic Regression Equation
The odds in favor of an event occurring is defined as the probability the event will occur divided by the probability the event will not occur.
Odds ratio: odds of a one-unit increase in only one of the independent variables.
Odds Ratio = odds1 / odds0








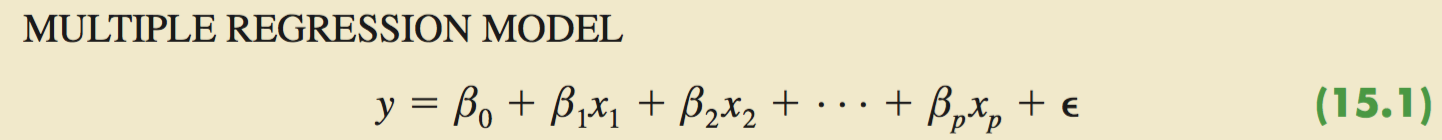


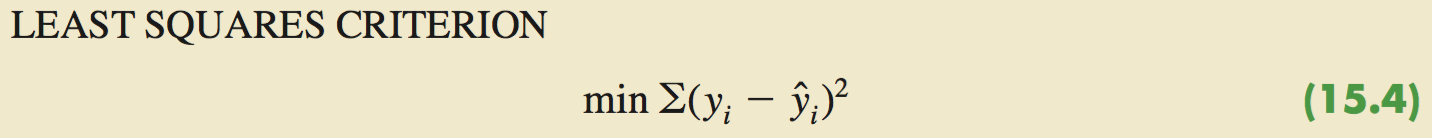








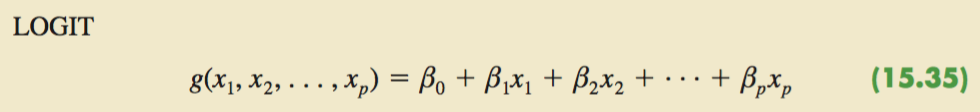
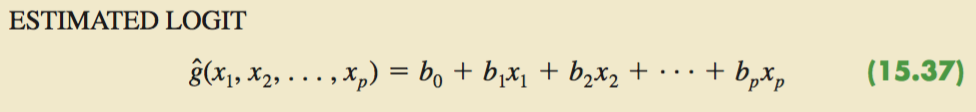
















 1223
1223

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








