CSDN笔记

拉普拉斯变换的收敛域(ROC)与逆变换(ILT)

1.是否可积即是否收敛(如果可收敛,面积/拉氏值即为收敛域)

（1）收敛的条件：e^(-jwt)积分为振荡函数

（2）常系数线性微分方程对应线性时不变系统，其分析步骤有三：

（3）拉氏逆变换（ILT）的方法：

传递函数的极点：s=-4,s=-1;

求解过程中令s=-4,s=-1解出A,B；

1.化简时采用欧拉公式的两个变形形式(要熟记！)进行化简，即为e^(i*狗)=cos(狗)+isin（狗）；

 传递函数(Transfer Function)与拉普拉斯变换

1.传递函数的推导

(1)卷积可以简单的理解为叠加的状态在未消失时再次叠加

 2.令u(t)=c时，u(t)=ce^(0),继续推导如下：

 

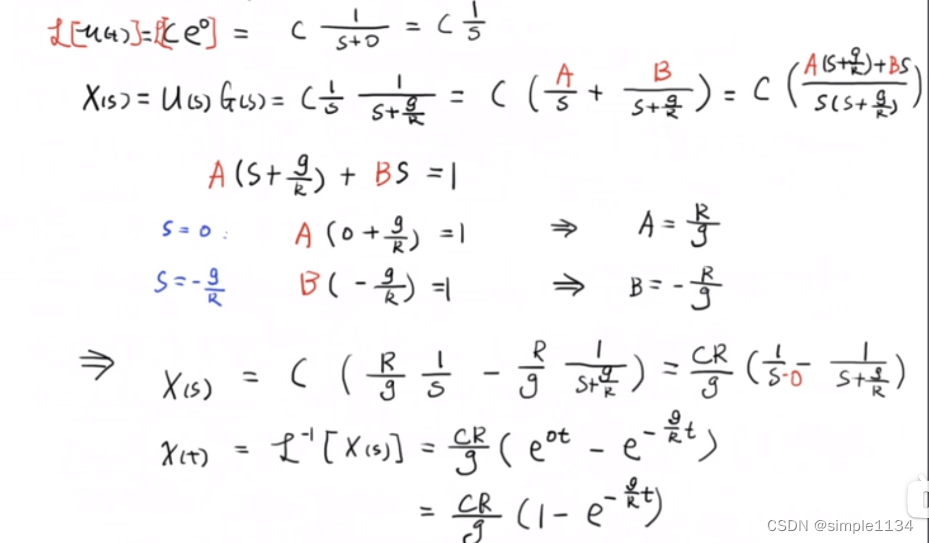
 将x（t）作图可得：

 由图可知x(t)是在一个范围内衰减的，观察e的指数0，-g/R,发现令u(s)*g(s)的分母部分=0时，得到极点s1=0,s2=-g/R,因此可得重要结论:通过控制系统极点，来控制系统输出。

 

稳定性分析 

由第一节可知开环闭环系统响应如下，给系统输入单位冲击响应就可以判断系统的稳定性，单位冲击响应的拉普拉斯变换是1，所以X(s)=G(s),对系统的稳定性分析变为对系统传递函数的分析。

 传递函数分子为零的点为零点，分母为零的点为极点

 从下图可以看出来，由于极点的正负，可以影响系统的稳定性

共轭复根的实部是负的，其输出函数为e^(-t)sin⁡(t+∅)。sin⁡(t+∅)和这两个函数相乘会趋于稳定，同理，如果实部为正，会让系统发散，为零则处于临界状态

 总结如下图为：如果极点为实数，落在左半平面稳定（红色），右半平面（蓝色）发散；如果为一对共轭复根，落在左半平面（棕色）一边震荡一边稳定，右半平面（绿色）一边震荡一边收敛；如果只有虚部（黄色），就是震荡的响应

所以，在设置控制器D的时候，是需要控制器的极点再左半平面，在现代控制理论中，研究的是状态矩阵的特征值，这些特征值实际上就对应着极点