机器学习模型可解释性进行到底 —— 从SHAP值到预测概率（二）

第一篇主要把SHAP值的各类图表操作方式进行展示：
机器学习模型可解释性进行到底 —— SHAP值理论（一）

接下来主要围绕一篇文章的内容展开【黑盒模型实际上比逻辑回归更具可解释性】

源代码部分：smazzanti/tds_black_box_models_more_explainable
自己的测试代码：mattzheng/ml_interpretability

非常有意思的一个案例，里面把SHAP值的解释性又增强了一步。

SHAP值对于人类来说是不可理解的(即使对于数据科学家来说也是如此)，概率的概念要容易理解得多。

所以文章将SHAP -> 预测概率进行迁移。

其他参考：
机器学习模型可解释性进行到底——特征重要性（四）
机器学习模型可解释性进行到底 ——PDP&ICE图（三）

---

---

1 一元插值

1.1 原文理论部分

想要从SHAP过渡到概率，最明显的方法是绘制相对于SHAP和(每个个体)的预测的生存概率(每个个体)。

很明显，这是一个确定性函数。也就是说，我们可以毫无差错地从一个量转换到另一个量。毕竟，两者之间的唯一区别是，概率必然在[0,1]，而SHAP可以是任何实数。因此:

其中f(.)是一个单调递增的s型函数，它将任意实数映射到[0,1]区间(为简单起见，f()可以是一个以[0,1]为界的普通插值函数)。

让我们以一个个体为例。假设已知除年龄外的所有变量，其SHAP和为0。现在假设年龄的SHAP值是2。

我们只要知道f()函数就可以量化年龄对预测的生存概率的影响：它就是f(2)-f(0)。在我们的例子中，f(2)-f(0) = 80%-36% = 44%

毫无疑问，生存的概率比SHAP值更容易被理解。

SHAP矩阵出发，应用以下公式就足够了：

得到下面的：

例如，拥有一张三等舱的票会降低第一个乘客的生存概率-4.48%(相当于-0.36 SHAP)。请注意，3号乘客和5号乘客也在三等舱。由于与其他特征的相互作用，它们对概率的影响(分别为-16.65%和-5.17%)是不同的。

1.2 解析映射函数

参考文章：Python：插值interpolate模块

文章中，所使用的SHAP -> 预测概率进行迁移的方法为：一维插值interp1d()

插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。

计算插值有两种基本的方法，

• 1、对一个完整的数据集去拟合一个函数；
• 2、对数据集的不同部分拟合出不同的函数，而函数之间的曲线平滑对接。

第二种方法又叫做仿样内插法，当数据拟合函数形式非常复杂时，这是一种非常强大的工具。

import numpy as np
from scipy import interpolate
import pylab as pl

x=np.linspace(0,10,11)
y=np.sin(x)

xnew=np.linspace(0,10,101)

pl.plot(x,y,'ro')
list1=['linear','nearest']
list2=[0,1,2,3]
for kind in list1:
    print(kind)
    f=interpolate.interp1d(x,y,kind=kind)
    #f是一个函数，用这个函数就可以找插值点的函数值了：
    ynew=f(xnew)
    pl.plot(xnew,ynew,label=kind)

pl.legend(loc='lower right')
pl.show()

来看一则例子，先是用interpolate.interp1d 拟合一个逼近函数，然后用该函数去拟合xnew
这里kind有两种逼近的方法：linear / nearest

官方的一元线性插值参考：
Scipy Tutorial-插值interp1d

---

2 实例测试：SHAP -> 预测概率

CatBoostClassifier模型对分类比较友好，同时内嵌了shap值计算。
大概的流程是：

• 创建catboost模型
• 使用模型预测，得到样本预测的：pred_cat
• 使用模型预测全样本的shap值：cat.get_feature_importance(data = Pool(X_all, cat_features=cat_features), type = 'ShapValues')
• 用一元插值函数拟合f(shap_sum，pred_cat)，其中shap_num代表每个样本shap值加总
• 利用上面函数拟合f(shap_sum - 特征值)，获得新的概率值，具体参考：

shap_df[feat_columns].apply(lambda x: shap_sum - x).apply(intp)\
                .apply(lambda x: probas - x)

2.1 细拆转化映射函数

来看一下笔者改进之后的转化函数，参考笔者代码：util.py：

from scipy.interpolate import interp1d
#probas_cat = pd.Series(cat.predict_proba(X_all)[:,1],index=X_all.index)

def shap2deltaprob_v2(shap_df, 
                   probas,
                   func_shap2probas = 'interp1d'):
    '''
    shap值 -> 映射到概率上面
    
    
    map shap to Δ probabilities
    --- input ---
    :features: list of strings, names of features
    :shap_df: pd.DataFrame, dataframe containing shap values
    :shap_sum: pd.Series, series containing shap sum for each observation
    :probas: pd.Series, series containing predicted probability for each observation
    :func_shap2probas: function, maps shap to probability (for example interpolation function)
    --- output ---
    :out: pd.Series or pd.DataFrame, Δ probability for each shap value
    '''
    
    feat_columns = shap_df.columns.to_list() # 模型的特征名称
    shap_sum = shap_df.sum(axis = 1)
    
    if func_shap2probas == 'interp1d' :
        shap_sum_sort = shap_sum.sort_values()
        probas_cat_sort = probas[shap_sum_sort.index]
        intp = interp1d(shap_sum_sort,
                        probas_cat_sort, 
                        bounds_error = False, 
                        fill_value = (0, 1))
    
    # 1 feature
    if type(feat_columns) == str or len(feat_columns) == 1:
        return probas - (shap_sum - shap_df[feat_columns]).apply(intp)
    # more than 1 feature
    else:
        return shap_df[feat_columns].apply(lambda x: shap_sum - x).apply(intp)\
                .apply(lambda x: probas - x)

拟合函数： interp1d(shap_sum_sort,probas_cat_sort)
代表拟合了一个映射函数：f(x -> y) => f(每个样本shap汇总 -> 预测概率 )，公式为：

现在函数核心是利用该映射函数，找到影响的impact概率，公式为：

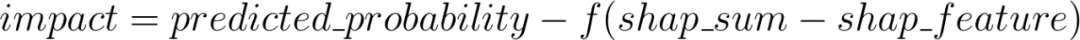
代码对应为：probas - (shap_sum - shap_df[feat_columns]).apply(intp)
也就是：
shap_sum - x -> ??，其中shap_num-x为shap增量

2.2 转化概率后如何解读——表格

直接贴原文啦

例如，拥有一张三等舱的票会降低第一个乘客的生存概率-4.48%(相当于-0.36 SHAP)。请注意，3号乘客和5号乘客也在三等舱。由于与其他特征的相互作用，它们对概率的影响(分别为-16.65%和-5.17%)是不同的。

2.3 转化概率后如何解读——边际效应

原文提及了，按照shap的计算方式，那么比如男/女特征，不同样本的shap值是不一样的，
那么就可以分组来计算一下平均数与标准差。

        count      mean       std
Sex                              
female  466.0 -0.005457  0.077510
male    843.0  0.000164  0.044532

这边笔者将原文进行了简单的微调：

def partial_deltaprob_v2(feature, X, dp_col, cutoffs = None ):
    '''
    return univariate analysis (count, mean and standard deviation) of shap values based on the original feature
    --- input ---
    :feature: str, name of feature,单个样本
    :X: pd.Dataframe, shape (N, P),全量的X，不是训练集
    :dp_col：shap计算之后全样本值
    :cutoffs: list of floats, cutoffs for numerical features,是否去掉一些特征
    --- output ---
    :out: pd.DataFrame, shape (n_levels, 3)
    '''
    # dp_col = shap2deltaprob(feature, shap_df, shap_sum, probas, func_shap2probas)
    dp_col_mean = dp_col.mean()
    dp_col.columns = 'DP_' + dp_col.columns
    out = pd.concat([X[feature], dp_col], axis = 1)
    if cutoffs:
        intervals = pd.IntervalIndex.from_tuples(list(zip(cutoffs[:-1], cutoffs[1:])))
        out[feature] = pd.cut(out[feature], bins = intervals)
        out = out.dropna()   
    out = out.groupby(feature).describe().iloc[:, :3]
    out.columns = ['count', 'mean', 'std']
    out['std'] = out['std'].fillna(0)
    return out

这里原文有：dp_col.name = 'DP_' + feature，那么一般是不会命名成功，会报错，因为一个数据表中有两个一样的col：

报错 ValueError: Grouper for 'NOX' not 1-dimensional

所以，笔者在py3.7需改成：dp_col.columns = 'DP_' + dp_col.columns

另外看一下画图函数:

import matplotlib.pyplot as plt

def plot_df(dp):
    # partial_deltaprob_v2 输出值进行画图
    plt.plot([0,len(dp)-1],[0,0],color='dimgray',zorder=3)
    plt.plot(range(len(dp)), dp['mean'], color = 'red', linewidth = 3, label = 'Avg effect',zorder=4)
    plt.fill_between(range(len(dp)), dp['mean'] + dp['std'], dp['mean'] - dp['std'],
                     color = 'lightskyblue', label = 'Avg effect +- StDev',zorder=1)
    yticks = list(np.arange(-.2,.41,.1))
    plt.yticks(yticks, [('+' if y > 0 else '') + '{0:.1%}'.format(y) for y in yticks], fontsize=13)
    plt.xticks(range(len(dp)), dp.index, fontsize=13)
    plt.ylabel('Effect on Predicted\nProbability of Survival',fontsize=13)
    plt.xlabel('Sex', fontsize=13)
    plt.title('Marginal effect of\nSex', fontsize=15)
    plt.gca().set_facecolor('lightyellow')
    plt.grid(zorder=2)

2.3.1 乘客年龄的边际效应

2.3.2 乘客票价的边际效应

2.3.3 交互作用：乘客票价 vs. 客舱等级

这里的图三代表两个变量的交互作用，其实也是，两变量分组汇总。

红线表示平均效应(一组中所有个体的年龄效应的均值)，蓝带(均值±标准差)表示同一组中个体年龄效应的变异性。变异是由于年龄和其他变量之间的相互作用。

这个方法的可提供的价值：

• 我们可以用概率来量化效果，而不是用SHAP值。例如，我们可以说，平均来说，60-70岁的人比0-10岁的人(从+14%到-13%)的存活率下降了27%
• 我们可以可视化非线性效应。例如，看看乘客票价，生存的可能性上升到一个点，然后略有下降
• 我们可以表示相互作用。例如，乘客票价与客舱等级。如果这两个变量之间没有相互作用，这三条线就是平行的。相反，他们表现出不同的行为。蓝线(头等舱乘客)的票价稍低。特别有趣的是红线(三等舱乘客)的趋势：在两个相同的人乘坐三等舱时，支付50 - 75英镑的人比支付50英镑的人更有可能生存下来(从-10%到+5%)。

3 案例

笔者把文章进行简单修改，是使用catboost的，记录在：catboost_test.py

还模拟了一个XGB的模型，可见：xgboost_test.py

# train an XGBoost model
import xgboost
import shap
import pandas as pd


# 获取数据
X, y = shap.datasets.boston()

# train an XGBoost model
model = xgboost.XGBRegressor().fit(X, y)

# 计算概率值
probas_xgb = pd.Series(model.predict(X),index=X.index)
probas_xgb

# 获得全样本的shap值
explainer = shap.Explainer(model)
shap_values = explainer(X)

shap_df = pd.DataFrame([list(shap_values[n].values)  for n in range(X.shape[0])],columns = X.columns )
shap_df

# shap值 映射向 概率
from util import shap2deltaprob_v2
shap_temp = shap2deltaprob_v2(shap_df, 
                   probas_xgb,
                   func_shap2probas = 'interp1d')
shap_temp


# 画出重点shap值
shap_temp = shap_temp.head().applymap(lambda x:('+'if x>0 else '')+str(round(x*100,2))+'%')

shap_temp.style.apply(lambda x: ["background:orangered" if float(v[:-1])<0 else "background:lightgreen"
                                for v in x], axis = 1)

# 影响分析
from util import partial_deltaprob_v2 ,plot_df

# 单特征分析
shap_temp = shap2deltaprob_v2(shap_df, 
                   probas_xgb,
                   func_shap2probas = 'interp1d')


feature = 'RAD' # 一个特征
dp_col = shap_temp
out = partial_deltaprob_v2(feature, X, dp_col, cutoffs = None )

plot_df(out)


# 特征交叉分析 - 分组汇总,不封装了...

4 SHAP值下：类别特征额外处理

参考文章:SHAP的理解与应用
里面有专门处理类别变量的方式，不过文章中的结论是，是否one-hot处理，差别蛮大，貌似我自己测试，没有差别，
可能是我哪一步出错了…没细究…
参考代码：lightgbm_test.py