可解释机器学习模型：解释SHAP分析的非技术指南

可解释机器学习模型：解释SHAP分析的非技术指南

参考:

1. 博客：https://www.aidancooper.co.uk/a-non-technical-guide-to-interpreting-shap-analyses/?xgtab&
2. 代码：https://github.com/AidanCooper/shap-analysis-guide/tree/main

1. 引言(Introduction)

随着可解释性成为机器学习项目越来越重要的要求，越来越需要将SHAP等技术的复杂输出传达给非技术利益相关者。

随着可解释性成为机器学习项目越来越重要的要求，人们越来越需要将模型解释技术的复杂输出传达给非技术利益相关者。SHAP（SHapley Additive exPlanations）可以说是解释机器学习模型如何进行预测的最强大的方法，但对于那些不熟悉该方法的人来说，SHAP分析的结果可能是不直观的。

本指南旨在为两个受众提供服务：

1. 对于数据科学家来说，本指南概述了一种结构化的方法，用于呈现SHAP分析的结果，以及如何向不熟悉SHAP的观众解释推荐的情节。
2. 对于那些需要能够理解SHAP输出而不是基本方法的人，本指南提供了关于如何解释常见的SHAP图并从中获得有意义的见解的全面解释。

本指南将清晰度置于严格的技术准确性之上。对于那些希望深入挖掘某些主题的人，提供了有用资源的链接。可以在GitHub上找到重现此分析的代码。

1.1. What is SHAP?

SHAP是一种解释机器学习模型如何进行个体预测的方法。SHAP将预测分解为来自模型的每个输入变量的贡献的总和${}^{[1，2]}$。对于数据（即行）中的每个实例，每个输入变量（也称为“特征”）对模型预测的贡献将根据该特定实例的变量值而变化。

为了理解这些贡献是如何结合起来解释预测的，有必要讨论机器学习模型的输出是什么样子的。

在机器学习回归模型的情况下，即预测连续结果的模型，输出只是预测值：例如房价或明天的温度。

图1。机器学习回归器和分类器模型的示例输出(预测), f(x)。对于分类器示例，将0和1之间的模型输出分数阈值设定为0.5，以产生二进元的预测。

对于机器学习分类器模型，即预测二元是/否结果的模型，情况稍微复杂一些。在这种情况下，模型输出0到1之间的分数，然后将其阈值设置为指定值（通常为0.5）。高于阈值的分数对应于阳性预测（例如肿瘤是恶性的），而低于该阈值的分数则对应于阴性预测（肿瘤是良性的）。这个分数可以松散地（但不是严格地，除非模型已经校准${}^{[3]}$）被视为一种概率，其中较高的分数对应于更有信心的积极预测，较低的分数对应着更有信心的消极预测。

A machine learning model’s prediction, f(x), can be represented as the sum of its computed SHAP values, plus a fixed base value, such that:
$$f(x)=basevalue+sum(SHAPvalues)$$

SHAP的输出是一个数据集，其维度与最初训练模型的维度相同(即它具有与列相同的输入变量和行相同的实例)。然而，此数据集不包含基础数据的值，而是包含SHAP值。至关重要的是，机器学习模型对每个实例的预测可以被再现为这些SHAP值的总和加上固定的基本值，使得模型输出，$f(x)=basevalue+sum(SHAPvalues)$。对于回归模型，基本值等于目标变量的平均值（例如数据集中的平均房价），而对于分类模型，基本价值等于阳性类别的流行率（例如数据集中恶性肿瘤的百分比）。正如我们将在下面的章节中看到的那样，SHAP值揭示了输入变量如何影响机器学习模型的预测的有趣见解，无论是在单个实例层面上，还是在整个群体中。

图2。使用SHAP作为事后解释技术来解释机器学习回归器的预测f(x)。

SHAP可以作为事后解释技术应用于任何机器学习模型，即在模型训练后应用，并且对算法本身是不可知的。也就是说，为基于树的模型（如随机森林和梯度增强树）计算SHAP特别有效${}^{[4]}$。

1.2. What can SHAP be used for?

SHAP量化了每个输入变量对模型进行预测的重要性。这可能是一个有用的理智检查，以确保模型的行为是合理的：模型是否利用了我们基于领域专业知识所期望的特征？这也是满足监管环境中 "解释权 "要求的一种方式^[5]。

偶尔，SHAP会在一个无害的特征和预测的结果之间浮现出异常强烈的关系。这通常是由于基础数据的问题，例如从被预测的目标变量到有关特征的信息泄露。因此，当模型具有可疑的高预测性能时，SHAP可以成为一个有用的诊断工具。

其他时候，这些令人惊讶的关系是合法的，可以作为假设生成的机制：即为什么这个特征有如此高的预测性，我们可以做什么来验证这个理论？

在从SHAP分析中获得洞察力时，应谨慎行事。重要的是，不要对某些特征导致某些结果的结论过度投入，除非实验是在因果框架内进行的（这种情况很少）^[6] 。SHAP只告诉你模型在它所训练的数据背景下的表现：它不一定揭示现实世界中变量和结果之间的真正关系。决策者经常被诱惑将SHAP分析中的特征视为可以操纵的拨盘，以设计特定的结果，因此必须传达这种区别。

2. SHAP Analysis Walk-Through

在这个SHAP分析的例子中，我们使用了一个描述波士顿506个房价实例的流行数据集的修改版^[7]。这是一个回归问题，任务是开发一个机器学习模型，根据12个特征预测连续的房价，这些特征在表1中列出。

图3显示了表1中特征的分布，以及机器学习回归器模型所预测的房价的目标值。房价的中位数是21200美元–这个数据毕竟是70年代的数据…!

图3.模型输入变量（又称 "特征"，左）的分布和被预测的目标房价的图表（右），数据集中有506个房屋实例。

SHAP是一种与模型无关的技术，可以应用于任何机器学习算法，所以模型开发过程的具体细节对本讨论并不重要。在这个演练中，我们训练了一个梯度提升树模型，这是一个强大的、流行的用于这类任务的算法。

2.1 Local interpretability: explaining individual predictions

解释对数据的个别实例的预测被称为局部可解释性(local interpretability)。SHAP用模型的每个输入变量的贡献来解释单个预测是如何得出的。这是一种高度直观的方法，可以产生简单但信息量大的输出。

2.1.1 Waterfall plots(瀑布图)

图4. 波士顿住房价格数据集中与预测房价中值相对应的单个案例的瀑布图示例。

瀑布图是对单一预测的最完整显示。在图4中，一个瀑布图的例子解释了每个特征对数据集中的中位价格房屋的预测的基本贡献。瀑布结构强调了正负贡献的相加性，以及它们是如何建立在基础值上以产生模型的预测结果f(x)的。

2.1.2 Force plots

瀑布图在解释一个预测时是广泛的，不放过任何细节，而力图则是同等的表示，以更浓缩的形式显示关键信息（图5）

图5. 与预测房价中位数相对应的力图或个案的例子。这完全等同于图4中的瀑布图，但对相同信息的看法更紧凑。

力量图对于同时检查数据的多个实例的解释是很有用的，因为它们的结构紧凑，可以将输出垂直堆叠起来，便于比较（图6）。

图6. 数据实例的力图示例，预测房价在第80（顶部）、第60、第40和第20（底部）百分位。注意：所有图中的基础值22,533美元是一致的（对数据的所有实例也是如此）。

2.3 Global interpretability: understanding drivers of predictions across the population

全局解释(global interpretation)方法的目标是描述机器学习模型在其输入变量值的整体分布方面的预期行为。通过SHAP，这一点可以通过汇总整个群体中单个实例的SHAP值来实现。

2.3.1 Bar plots

用SHAP进行全面解释的最简单的起点是检查所有数据中每个特征的平均绝对SHAP值。这平均量化了每个特征对预测房价的贡献大小（正或负）。平均绝对SHAP值越高的特征就越有影响力。平均绝对SHAP值基本上可以替代更传统的特征重要性测量，但有两个关键优势：

• 平均绝对SHAP值在理论上更加严谨，并且与哪些特征对预测影响最大有关（这通常是我们感兴趣的）。传统的特征重要性是以更抽象和特定算法的方式来衡量的，并由每个特征对模型预测性能的改善程度决定。
• 平均绝对SHAP值有直观的单位–在这个例子中，它们被量化为美元，像目标变量一样。特征的重要性通常以反直觉的单位表示，基于复杂的概念，如树形算法的节点杂质。

图7. 条形图显示每个变量的平均绝对SHAP值。这向我们展示了各变量对模型预测房价的排名和相对影响。

如图7所示，平均绝对SHAP值通常显示为条形图，按其重要性排列特征。要检查的关键特征是特征的排序和平均绝对SHAP值的相对大小。这里我们看到，工薪阶层的百分比是最有影响力的变量，对每个预测的房价平均贡献了±3,821美元。相比之下，信息量最小的变量，查尔斯河，只贡献了±13美元–考虑到它在93%的数据集中有相同的0值，这并不令人惊讶（见图3）。

2.3.2 Beeswarm plots(蜂巢图)

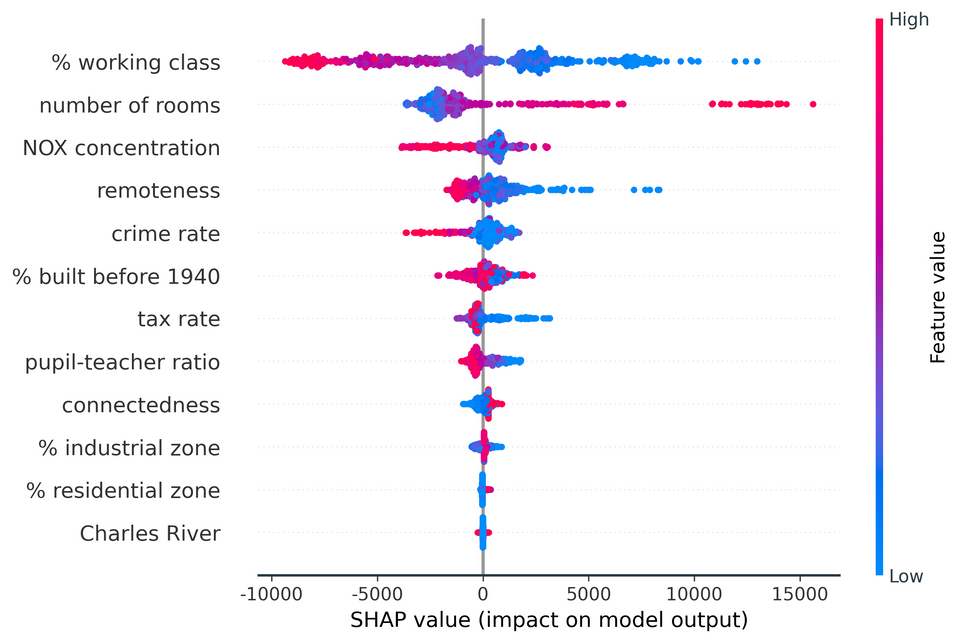
SHAP特征重要性柱状图是一种优于传统替代方法的方法，但孤立地看，除了其更严格的理论基础外，它们几乎没有提供额外的价值。蜂巢图是一种更复杂、信息更丰富的SHAP值显示，它不仅揭示了特征的相对重要性，而且揭示了它们与预测结果的实际关系。

图8.蜂群图，按平均绝对SHAP值排列。这提供了一个丰富的概述，说明在所有的数据中，变量是如何影响模型的预测的。

图9显示了我们的波士顿房价例子的蜂巢图。之前的柱状图没有告诉我们每个特征的基本值与模型预测的关系，现在我们可以研究这些关系。

例如，我们看到，较低的工薪阶层百分比值具有正的SHAP值（向右延伸的点越来越蓝），较高的工薪阶层百分比值具有负的SHAP值（向左延伸的点越来越红）。这表明，工人阶级较多的地区的房屋预测价格较低。房间数的情况正好相反–房间数越多，房价预测值就越高。

点的分布也可以是有信息的。对于犯罪率，我们看到一个密集的低犯罪率实例集群（蓝点），其SHAP值较小但为正。高犯罪率的实例（红点）进一步向左延伸，表明高犯罪率对价格的消极影响比低犯罪率对价格的积极影响更大。

图9.如果需要，可以对条形图和蜂巢图进行调整。顶部：条形图显示每个变量的最大（而不是平均）绝对SHAP值。底部：使用绝对SHAP值的蜂群图--是简单的条形图和复杂的蜂群图之间的折中。

尽管图7和图8中的条形图和蜂群图是迄今为止最常用的SHAP值的总体表示方法，但也可以创建其他的可视化图。图9强调了两种变化：一种是采用最大而非平均的绝对SHAP值；另一种是条形图和蜂群图的混合。

2.3.3 Dependence plots(依赖图)

蜂巢图是信息密集型的，可以同时提供许多特征的SHAP值的广泛概述。然而，为了真正理解一个特征的值与模型预测结果之间的关系，有必要检查依赖图。

图10显示了前五个特征的依赖图，并揭示了SHAP值和变量值之间的关系在每个特征中都有很大的不同。工薪阶层在整个数值范围内表现出一个负的、近乎线性的趋势。房间数的SHAP值在4到6.5个房间之间具有可比性，但随后急剧增加。对于氮氧化物浓度，其分布是不连贯的，在千万分之0.68两侧的变量值有明显的分离。

图10.由平均绝对SHAP值决定的前五个最重要特征的依赖图。

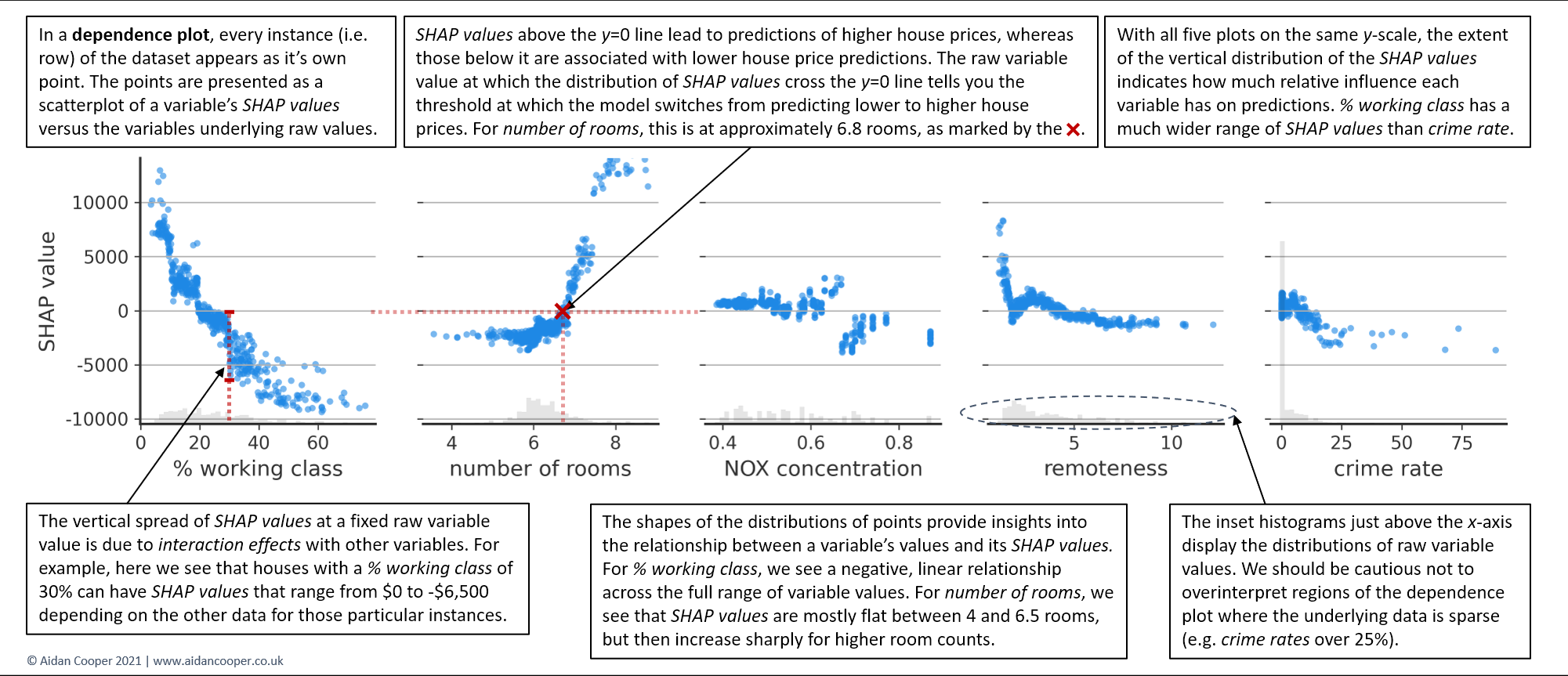
在固定变量值中看到的SHAP值的垂直离散是由于与其他特征的**交互效应(interaction effects)**造成的。这意味着一个实例对某一特征的SHAP值并不完全取决于该特征的值，而且还受到该实例其他特征值的影响。如图11所示，依存关系图通常是以强交互特征的值来表示的。对于这个房屋定价数据集来说，交互作用并不特别突出，但有些案例研究的特征之间有戏剧性的交互作用^[8] 。

图11.以氮氧化物浓度表示的工人阶级百分比的依赖图，这是工人阶级百分比与之有最强互动效应的特征。

3. 结论(Conclusion)

SHAP是一种强大的机器学习解释技术，能够产生大量复杂的分析输出。在构建将SHAP结果传达给利益相关者的故事时，应仔细考虑，以确保结论是有效的，并理解该技术的局限性。我希望本指南中的建议和解释能提供一个可操作的框架，帮助您的SHAP分析产生预期的影响。