David Silver《Reinforcement Learning》课程解读—— Lecture 4： Model-Free Prediction

David Silver《Reinforcement Learning》课程解读—— Lecture 4： Model-Free Prediction

DP动态规划能够解决已知environment的MDP问题，即已知$\ S,A,P,R,γ$，根据是否已知policy又将问题划分为prediction和control的问题。本质上来说这种known MDP问题已知environment即转移矩阵与reward函数。

但是很多问题中environment未知，不清楚做出了某个action之后会变到哪个state，也不知道这个action好不好，即说不清environment体现的model是什么。

这种情况下需要解决的prediction和control问题即model-free prediction和model-free control。<该问题只能从与environment交互得到的experience中获取信息>

本节即针对未知environment的policy evaluation，在给定policy下，求取state的value function是多少？

episode：从某个状态开始执行到终止状态的一次遍历$S_1,A_1,R_2,···，S_k$称为episode，已知很多episodes。

目录：

• Introduction
• Monto-Carlo Learning
• Temporal-Difference Learning
• TD(λ)

---

1. Introduction

1. Model-Free prediction
   
   • estimate the value function of an unknown MDP
2. Model-Free control
   
   • optimize the value function of an unknown MDP

---

2. Monte-Carlo Learning

1. 特点
   
   • 直接从experience的episode中学习
   • 不需要MDP的transition、rewards
   • 主要思想：value = mean return，即反复测试求平均。

2. Monte-Carlo Policy Evaluation

   • 基本内容
     
     • 目标：在策略π下，从experience的episodes中学到$v_π$
     • 已知：
       
       • a. return是所有的折扣回报之和
         $$\begin{align*} G_{t}= R_{t+1}+\gamma R_{t+2}+\cdot \cdot \cdot +\gamma^{k} R_{t+k+1}=\sum_{k=0}^{\infty }\gamma^{k} R_{t+k+1} \end{align*}$$
       • b. value function 是return的期望值（第二节中，每个state的value function是return的期望值）
         $$\begin{align*} v_{\pi }\left ( s \right )=E_{\pi }\left [ G_{t}|S_{t}=s \right ] \end{align*}$$
     • 关键：与第二节讲到的不同，Monte-Carlo policy 假设每个状态的value function取值等于多个episodes的return $G_t$d的平均值而非期望值，即在Monte-Carlo policy evaluation的假设下，值函数的取值从期望简化成了均值。这就需要每个episode是完整的流程，即一定要执行到终止状态。
     • 由于每一步的reward都知道，则意味着每一步的return $G_{t}$都可以计算出来。因此，通过反复测试，这样很多状态就会被遍历到，而且不止一次，那么每次就可以把在状态下的return求取平均值。当episode无限大时，得到的数据也就接近于真实的数据。Monte-Carlo方法就是使用统计学的方法来取代Bellman方法的计算方法。
     • 有两种访问次数的记录方式，一种是在一个episode中只记录第一次访问到的s，一种是一个episode中每次访问到s都记录下来。
     • First-Visit MC Policy Evaluation，每一次的episode中state只使用第一次到达的t来计算return
       
     • Every-Visit MC Policy Evaluation，每一次的episode中state只要访问到就计算return求平均
       

   • 特点：可以看到蒙特卡洛方法是极其简单的。但是缺点也是很明显的，需要尽可能多的反复测试，而且需要到每一次测试结束后才来计算，需要耗费大量时间。“AlphaGo就是使用蒙特卡洛的思想。不是蒙特卡洛树搜索，而是说在增强学习中使用蒙特卡洛方法的思想。AlphaGo每次也是到下棋结束，而且只使用最后的输赢作为return。所以这也是非常神奇的事，只使用最后的输赢结果，竟然能够优化每一步的走法。”

   • Incremental Monte-Carlo

     • Incremental Mean
       序列$\left \{ x_{1},x_{2},\cdot \cdot \cdot \right \}$的均值$\left \{ u_{1},u_{2},\cdot \cdot \cdot \right \}$可以增量式增加
       

       $$\begin{eqnarray} u_{k} &=&\frac{1}{k}\sum_{j=1}^{k}x_{j}\\ &=&\frac{1}{k}\left ( x_{k}+ \sum_{j=1}^{k-1}x_{j}\right )\\ &=&\frac{1}{k}\left ( x_{k}+\left ( k-1 \right )u_{k-1} \right )\\ &=&u_{k-1}+\frac{1}{k}\left ( x_{k}-u_{k-1} \right ) \end{eqnarray}$$

     • Incremental Monte-Carlo Updates

       • Updates V(s) incrementally after episode $S_1, A_1, R_2, ···,S_T$。
       • 针对每一次新的访问，先次数加1，$N(S_t)=N(S_t)+1$，然后更新$V(S_t)=V(S_t)+\frac{1}{N(S_t)}(G_t-V(S_t))$
       • 在解非固定问题时，可以将$\frac{1}{N(S_t)}$设置为一个常数$\alpha$，即$V(S_t)=V(S_t)+\alpha(G_t-V(S_t))$.

---

3. Temporal-Difference Learning

1. 思想
   基于Bootstrapping思想，即在中间状态中会估计当前获得的return值，并更新之前状态能获得的return，因此它不需要走完一个episode的全部流程。而前面分析的蒙特卡洛方法，其一个特点就是需要运行完整个episode从而获得准确的result。但是往往很多场景下要运行完整个episode是很费时间的
2. 特点
   
   • 直接从experience的episode中学习
   • 不需要MDP的transitions、rewards
   • 通过bootstrapping从不完整的episode中学习
     bootstraping。即通过估计的方法来引导计算。那么蒙特卡罗不使用bootstraping，而TD使用bootstraping。
   • 每一步都可以更新，这是显然，也就是online learning，学习快
   • 从一个猜测更新到另一个猜测
   • 可以面对没有结果的场景，应用范围广
3. TD vs MC
   
   • 目标：learn $v_\pi$ online from experience under policy $\pi$.
   • Incremental every-visit Monte-Carlo
     根据真实的 reward $G_t$更新 $V(S_t)$:
     $$\begin{eqnarray}V(S_t)=V(S_t)+\alpha(G_t-V(S_t))\end{eqnarray}$$
   • Simplest temporal-difference learning algorithm: TD(0)
     根据估计的return更新$V(s_t)$, 估计return：$R_{t+1}+\gamma V(S_t+1)$:
     $$\begin{eqnarray} V(S_t)=V(S_t)+\alpha(R_{t+1}+\gamma V(S_t+1)-V(S_t))\end{eqnarray}$$
     其中，$R_{t+1}+\gamma V(S_t+1)$是 TD target,
     $\delta _{t}=R_{t+1}+\gamma V(S_t+1)-V(S_t)$是 TD error, 代表了估计前后return的差值
   • 平衡Bias/Variance是机器学习比较经典的一个问题，bias是指预测结果与真实结果的差值，variance是指训练集每次预测结果之间的差值，bias过大会导致欠拟合它衡量了模型是否准确，variance过大会导致过拟合衡量了模型是否稳定。
   • TD算法的相对缺点：因为TD target是估计值，估计是有误差的，这就会导致更新得到value是有偏差的。很难做到无偏估计。
   • TD算法的相对优点：TD target 是每一个 step 进行估计的，仅最近的动作对其有影响，而 MC 的 result 则受到整个时间片中动作的影响，因此 TD target 的方差 variance 会比较低，也就是波动性小。
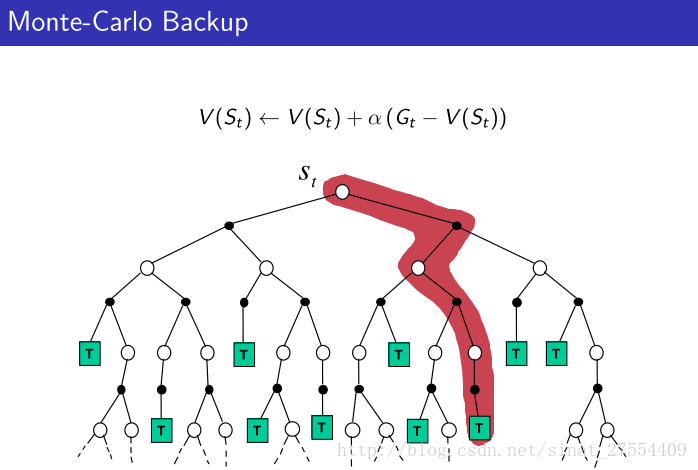
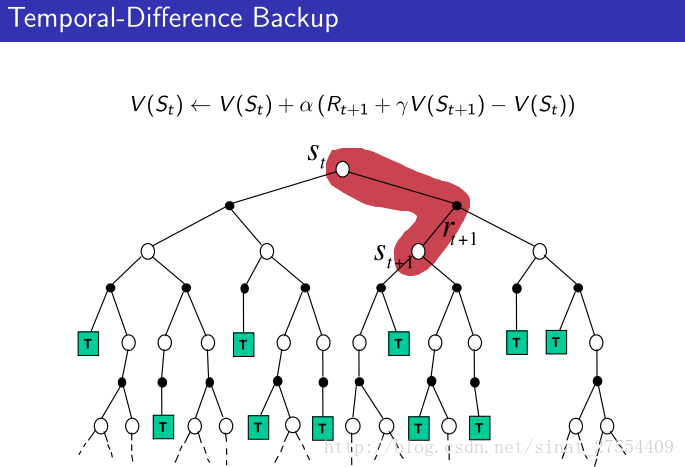
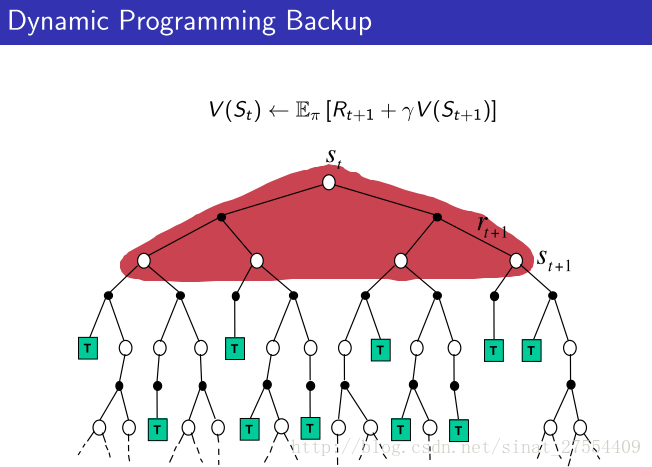
   • 具体对比如下图所示：
     
   • 在David Silver的课件中，有三张图，很直观地对比了MC，TD以及DP的不同：
     
     
     
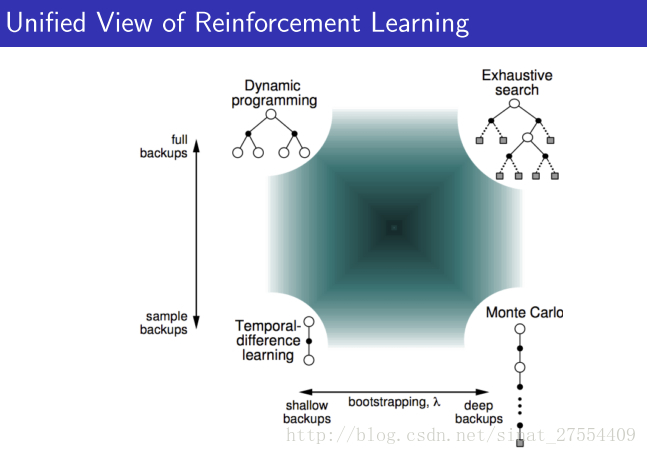
     从上面可以很清楚的看到三者的不同。DP就是理想化的情况，遍历所有。MC现实一点，TD最现实，但是TD也最不准确。但是没关系，反复迭代之下，还是可以收敛的。
   • 整个增强学习算法也都在上面的范畴里：
     
     
   • 上面的图是用Policy Evaluation解决强化学习问题的一些算法的区别与相关性，最左边的竖线表示如果考虑了所有的可能发生的情况那么就是动态规划，如果只考虑了部分采样那么就是时序差分。下面的横线表示如果考虑了一次episode中全部的动作就是Monte-Carlo，如果只考虑部分动作就是时序差分。如果又考虑全部情况又考虑每一种情况的全部动作就是穷举。

---

4. TD$\left ( \lambda \right )$

1. 思想
   
   • $TD\left ( 0 \right )$: 在某个状态$S$下执行某个动作后转移到下一个状态${S}'$时，估计${S}'$的return再更新S。
   • 若$S$之后执行2次动作转移到${S}''$时再返回来更新$S$的值函数，那么就是另外一种形式，从而根据step的长度n可以扩展TD到不同形式，当step的长度达到episode的终点时就变成了MC，从而得到统一公式如下：
     $$\begin{align*} G_{n}= R_{t+1}+\gamma R_{t+2}+\cdot \cdot \cdot +\gamma^{n-1} R_{t+n}+r^{n} V(S_{t+n}) \end{align*}$$

$$\begin{align*} V\left ( S_{t} \right )=V\left ( S_{t} \right )+\alpha \left ( G_{t}^{\left ( n \right )}-V\left ( S_t \right ) \right )\end{align*}$$

• 
  
  • $TD\left ( \lambda \right )$: 若将不同的n对应的return平均一下，就能获得更加鲁邦的结果，而为了有效地将不同return结合起来，对每个return都赋予了一个权重$1-\lambda,\left ( 1-\lambda \right )lambda,\cdot \cdot \cdot ,\left ( 1-\lambda \right )\lambda^{n}$，参数是$lambda$，这样又可以得到一组更新value function公式：
    $$\begin{align*}G_{t}^{\lambda }=\left ( 1-\lambda \right )\sum_{n=1}^{\infty }\lambda ^{n-1}G_{t}^{n} \end{align*}$$

$$\begin{align*}V\left ( S_t \right )=V\left ( S_t \right )+\alpha \left ( G_{t}^{\lambda }-V\left ( S_t \right ) \right ) \end{align*}$$