标量、向量、矩阵、张量之间的区别和联系

前言

深度学习的表现之所以能够超过传统的机器学习算法离不开神经网络，然而神经网络最基本的数据结构就是向量和矩阵，神经网络的输入是向量，然后通过每个矩阵对向量进行线性变换，再经过激活函数的非线性变换，通过层层计算最终使得损失函数的最小化，完成模型的训练。所以要想学好深度学习，对这些基础的数据结构还是要非常了解。

标量

标量(scalar)：一个标量就是一个单独的数(整数或实数)，不同于线性代数中研究的其他大部分对象(通常是多个数的数组)。标量通常用斜体的小写字母来表示，例如：$x$，标量就相当于Python中定义的

x = 1

向量

向量(vector)：一个向量表示一组有序排列的数，通过次序中的索引我们能够找到每个单独的数，向量通常用粗体的小写字母表示，例如：$\mathbf{x}$，向量中的每个元素就是一个标量，向量中的第$i$个元素用$x_i$表示，向量相当于Python中的一维数组

import numpy as np
#行向量
a = np.array([1,2,3,4])

矩阵

矩阵(matrix)：矩阵是一个二维数组，其中的每一个元素由两个索引来决定($A_{i,j}$)，矩阵通常用加粗斜体的大写字母表示，例如：$\mathbf{X}$。我们可以将矩阵看做是一个二维的数据表，矩阵的每一行表示一个对象，每一列表示一个特征。在Python中的定义为

import numpy as np
#矩阵
a = np.array([[1,2,3],[4,5,6],[7,8,9]])

张量

张量(tensor)：超过二维的数组，一般来说，一个数组中的元素分布在若干维坐标的规则网格中，被称为张量。如果一个张量是三维数组，那么我们就需要三个索引来决定元素的位置($A_{i,j,k}$)，张量通常用加粗的大写字母表示，例如：$\mathbf{X}$

import numpy as np
#张量
a = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])

标量向量矩阵张量之间的联系

通过上面的介绍可以总结一下，标量是0维空间中的一个点，向量是一维空间中的一条线，矩阵是二维空间的一个面，三维张量是三维空间中的一个体。也就是说，向量是由标量组成的，矩阵是向量组成的，张量是矩阵组成的。

用一个比较通俗的例子可以概括为：假设你手中拿着一根棍子，标量就是我们只知道棍子的长度，但是不知道棍子指向的方向。向量就是我们除了知道棍子的长度之外还知道棍子指向的是左边还是右边，矩阵就是除了知道向量知道的信息外还知道棍子是朝上还是朝下，张量就是除了知道矩阵知道的信息外还知道棍子是朝前还是朝后。

线性代数常用的运算

一、向量的运算

1.点积

点积(dot product)又被称为数量积(scalar product)或者内积(inner product)：是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。

代数意义

两个向量$a(a_1,a_2,\dots ,a_n)$和$b(b_1,b_2,\dots ,b_n)$的点积定义为：$a\cdot b=a_1{b}_1+a_2{b}_2+\dots \dots +a_n{b}_n$，使用矩阵乘法并把（纵列）向量当作n×1 矩阵，点积还可以写为：$a\cdot b=a^T\ast b$，这里的$a^T$指示矩阵$a$的转置。

import numpy as np
a = np.array([1,2,3])
b = np.array([3,2,1])
#向量的点积运算
print(np.dot(a,b))#10

几何意义

除此之外，向量积还有另一种定义$\vec{a}\cdot \vec{b}=|\vec{a}|\ast |\vec{b}|\ast cos\theta$，该定义只对二维和三维空间有效，$|\vec{a}|$和$|\vec{b}|$表示向量的长度，$\theta$表示向量之间的夹角。

这个运算可以简单地理解为：在点积运算中，第一个向量投影到第二个向量上（这里，向量的顺序是不重要的，点积运算是可交换的），然后通过除以它们的标量长度来“标准化”。这样，这个分数一定是小于等于1的，可以简单地转化成一个角度值。利用向量积的几何意义，我们可以用来计算两个向量之间的夹角。

2.外积

设向量$\vec{c}$由两个向量$\vec{a}$与$\vec{b}$按下列方式定出：$\vec{c}$的模$|c|=|a||b|sin<a,b>$ $\vec{c}$的方向垂直于$\vec{a}$与$\vec{b}$所决定的平面（即$\vec{c}$既垂直于$\vec{a}$，又垂直于$\vec{b}$），$\vec{c}$的指向按右手规则从$\vec{a}$转向$\vec{b}$来确定。

那么，向量$\vec{c}$叫做向量$\vec{a}$与$\vec{b}$的外积，记作$\vec{a}\times \vec{b}$，即$\vec{c}=\vec{a}\times \vec{b}$ 。$|\vec{a}\times \vec{b}|$的值与以$\vec{a}$，$\vec{b}$为邻边的平行四边形的面积的值相同。一般地，向量外积的研究仅限于三维空间中

import numpy as np

a = np.array([0,2])
b = np.array([3,3])
#向量的外积
c = np.cross(b,a)
print(c)

通过外积我们可以用来快速求解平行四边形或三角形的面积，需要注意的是在计算向量积时候，向量之间的顺序，顺序相反会得到相反的结果(正数和负数)，判断方向时采用右手定则。

3.向量的范数

定义一个向量，$x=[x_1,x_2,...x_n]$

• 向量的1范数：向量中各个元素绝对值之和，$||x|{|}_1={\sum }_{i=1}^N|x_i|$
• 向量的2范数：向量中每个元素的平方和的平方根，$||x|{|}_2=\sqrt{{\sum }_{i=1}^N{x}_i^2}$
• 向量的负无穷范数：向量中所有元素的绝对值中最小的，$||x|{|}_{-\infty }=\underset{1\le x\le N}{\min }|x_i|$
• 向量的正无穷范数：向量中所有元素的绝对值中最大的，$||x|{|}_{\infty }=\underset{1\le x\le N}{\max }|x_i|$
• 向量的$p$范数：向量中每个元素的$p$次方和的$1/p$次幂，$||x|{|}_p=({\sum }_{i=1}^N|x{|}^p{)}^{1/p}$

二、矩阵的运算

1 .转置

转置(transpose)：是矩阵的重要操作之一。矩阵的转置是以对角线为轴的镜像，这条从左上角到右下角的对角线被称为主对角线(main diagonal)。如下图所示

其实就是将原矩阵的行变成了转置矩阵的列或将原矩阵的列变成转置矩阵的行。

2.矩阵的范数

定义一个矩阵${\mathbf{A}}_{mn}=\left\{\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right\}$

• 矩阵的1范数(列范数)：对矩阵每一列上的元素绝对值求和，再从中取一个列和最大的值，$||\mathbf{A}|{|}_1=\underset{1\le j\le n}{\max }{\sum }_{i=1}^m|a_{ij}|$
• 矩阵的2范数：矩阵${\mathbf{A}}^T\mathbf{A}$的最大特征值的平方根，$||\mathbf{A}|{|}_2=\sqrt{{\lambda }_{max}({\mathbf{A}}^T\mathbf{A})}$，式中的${\lambda }_{max}({\mathbf{A}}^T\mathbf{A})$为${\mathbf{A}}^T\mathbf{A}$的特征值绝对值最大的值，关于矩阵的特征值介绍将会在下一篇文章中详细介绍
• 矩阵的无穷范数(行范数)：对矩阵每一行的元素绝对值求和，再从中取一个行和最大的值，$||\mathbf{A}|{|}_{\infty }=\underset{1\le i\le m}{\max }{\sum }_{j=1}^n|a_{ij}|$
• 矩阵的核范数：矩阵的奇异值之和，这个范数可以用低秩表示
• 矩阵的$L_0$范数：矩阵的非0元素的个数，通常用它来表示稀疏度，$L_0$范数越小，0元素越多，矩阵就越稀疏。
• 矩阵的$L_1$范数：矩阵中的每个元素的绝对值之和，它是$L_0$范数的最优凸近似。
• 矩阵的$F$范数：矩阵的各个元素的平方之和再开平方根，通常也称为矩阵的$L_2$范数。
• 矩阵的$L_{21}$范数：矩阵先以每一列为单位，求每一列的$L_2$范数，再将得到的结果求$L_1$范数，所以它是介于$L_1$和$L_2$之间的一种范数。

3.常见的矩阵

• 方阵：也就方形矩阵，矩阵的列数与行数相等
• 对称矩阵：对称矩阵是一个方阵，矩阵的元素关于对角线对称，它的转置和自身相等，即$A=A^T$
• Jacobian矩阵：Jacobian矩阵是函数的一阶偏导数以一定方式排列成的矩阵
• 单位矩阵：主对角线上的元素都为1，其余元素全为0的n阶矩阵称为n阶单位矩阵，记为$I_n$或$E_n$ ，通常用$I$或$E$来表示
• 正交矩阵：如果$A{A}^T=I_n$，则$A$就被称为正交矩阵

4.矩阵的乘法

矩阵乘法：是最常见的矩阵乘积，两个矩阵相乘，必须要满足前一个矩阵的列数等于后一个矩阵的行数，一个$m\times p$的矩阵乘以一个$p\times n$会得到一个$m\times n$的矩阵。运算规则如下

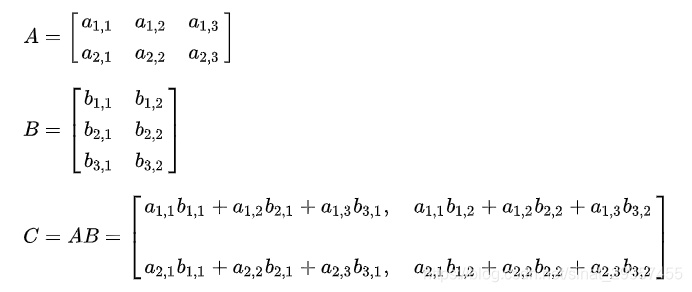
numpy的实现如下，和向量积一样

import numpy as np

a = np.array([[1,2,3],
              [-1,3,-2]])
b = np.array([[1,2],
              [3,4],
              [1,3]])
#矩阵相乘
print(np.dot(a,b))#或者使用np.matmul(a,b)
"""
[[10 19]
 [ 6  4]]
"""

5.矩阵哈达马积

哈达马积（Hadamard product）：也叫矩阵的元素相乘，矩阵对应元素相乘，两个矩阵在进行元素相乘的时候必须要有相同的行数和列数，计算公式如下

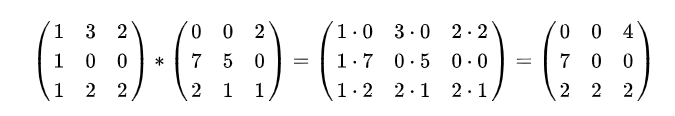
在Python中计算两个矩阵元素相乘的乘积直接相乘即可，如果两个相乘的矩阵行数和列数不相等会报错，相乘的时候其中一个可以是标量或向量，会自动使用广播，标量乘以矩阵中的所有元素，相当于对矩阵的元素做一个缩放

import numpy as np

a = np.array([[1,2],[3,4]])
b = np.array([[2,2],[1,3]])
#矩阵的元素相乘
c = a * b
print(c)
"""
[[ 2  4]
 [ 3 12]]
"""
#矩阵的广播
d = a * 2
print(d)
"""
[[2 4]
 [6 8]]
"""
d = a * np.array([1,2])
print(d)
"""
[[1 4]
 [3 8]]
"""

6.克罗内克积

克罗内克积（Kronecker Product）：克罗内克积是两个任意大小的矩阵间的运算，符号记作$\otimes$ 。克罗内克积也被称为直积或张量积。计算过程如下例所示：