ADAS倒车雷达超声波传感器elmos524.03驱动

最近一直在思考一个问题，什么是知识，什么是能力，自己的价值在哪里，感觉自己做笔记做的太少，燕过却不留声。最近也想总结下自己到底做过什么。固以此篇献给做汽车电子的朋友，以及想以超声波作为工程化落地的道友们。如有不对之处，欢迎指教。

话不多说，测距大多采用的方式都是”飞行时间法“，即获取某种信号，在介质中传播所用的时间。计算出距离，d = vt/2. 道理很简单。下边就详细说下，基于Elmos524.03芯片的倒车雷达如何工作的。以及工程化的处理方法。

工作原理

集成芯片Elmos524.03有发射回路和接收回路，我根据数据手册画了个草图：

芯片会产生固有频率的电压信号，信号通过引脚DRV1、2输出给外部压电陶瓷片，产生固定频率的机械波，也就是所谓的超声波，超声波遇到障碍物时会反射，反射信号经过AINS、D引脚进入芯片，在芯片内部先后经过GAIN放大，滤波然后进入比较器，滤波后的信号（signal）同预先设定的阈值（threshold）比较产生信号输出。此信号需要重点关注。

基于这个内部的工作原理，我也画了草图表示信号在单片机口的上表现形式，如下：

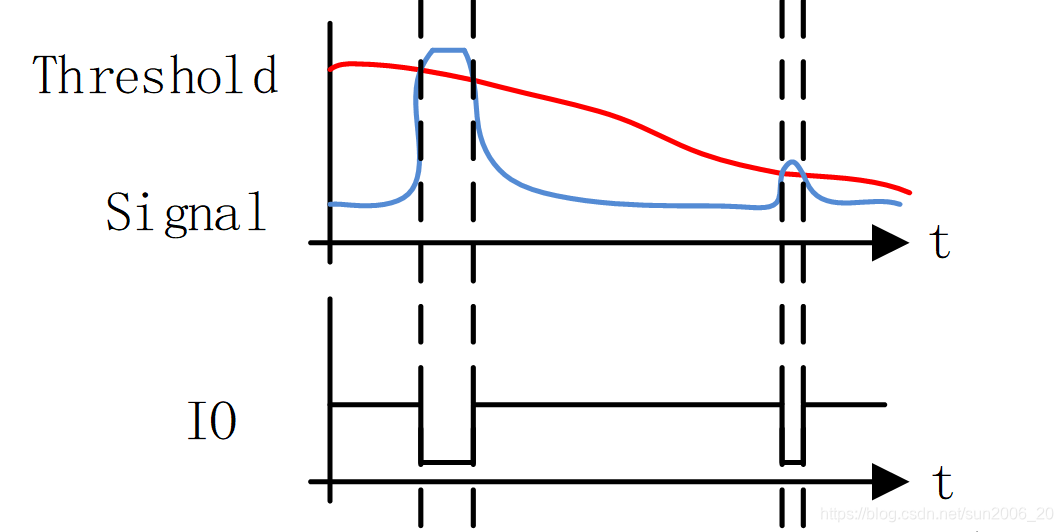
signal信号为模拟信号，IO输出的信号才是软硬件接口信号。

硬件接口

如果是探头供应商，则对探头的硬线比较了解，如果是采购别人的基于Elmos524.03芯片的探头，一般情况下都是三线连接，

 

Vsup：供电电压电源+，GND ：电源地  DATA：即为信号接口。

这里需要说明一点探头与ECU之间的接口虽为一根线，但与MCU之间的接口会是两根线，一根接IO输出，一根接捕获输入。实现单线双向IO的控制信号和反馈信号的传输。

软件接口

既然为单线连接，数据通过单线传输，所以就有自己的通信协议格式。Elmos524.03是采用脉宽编码进行通信的。

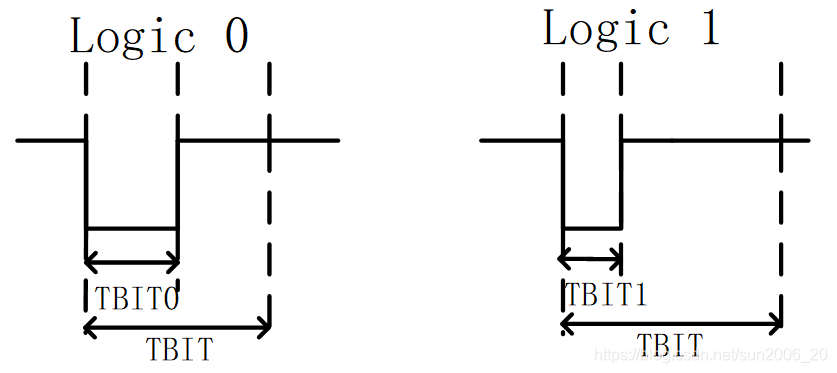
这些命令数据手册上都有说明，就不一一叙述。可以查看数据手册。重要的一点就是在数据传输的时候要保证数据的正确性，脉宽是控制在误差范围内。

实现这些命令可以采用定时器的方式。可以准确输出想要的脉冲命令。

一些复杂的命令也是几个简单的命令组合而成的。写配置/读状态/写EEPROM/读EEPROM等。

参数配置

配置的参数，其实就是对芯片原理中的几个信号处理的过程进行配置。大致有三个。

驱动电流/接受增益/阈值

对应的数据手册中都有说明，可以按照数据手册进行操作。这里需要说明的是 在进行软件编码的时候需要对这个参数做全覆盖。几个参数也是配合使用的。

信号捕获

关于信号的捕获，这里简单说下，可以将信号线上所有的信号进行记录，以便编码时对捕获的信号进行处理的时候，能够得到足够多的信息。

信号简单处理

对IO口上的信号进行数据处理，首先做简单的运算，对捕获的信号进行原始的运算，还原物理现场，还原信号线上的信号跳变情况。作为后续处理的输入。

信号比对--抗干扰

对于基本操作就不多做叙述，这里说下如何对障碍物检测的准确度进行保证，最大程度上避免误报。其中一个方法就是比对。

可以对同一个障碍物的回波进行多次比对。进而确认。并且可以达到去除噪声的目的。我画了一个草图如下：

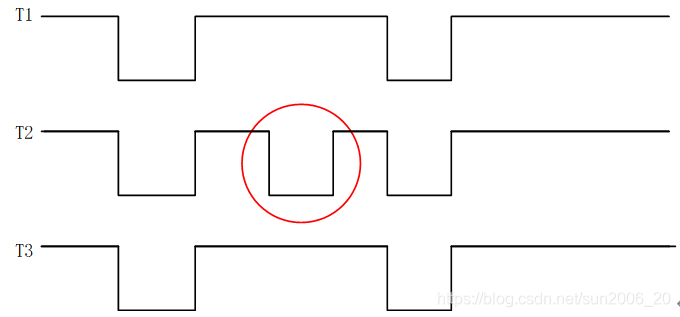
可以对两个周期或者三个周期内的测试信号进行比对。将干扰的回拨进行去除。如图中红色圈即为，噪声。或认为是无效目标。

信号分析

对比对后的信号进行分析。

分析信号对应的操作是在进行什么工作。简单举例来说，可以捕获到发送命令，然后判断发送命令是否正确，达到验证的目地。

对命令的验证需要有一定的范围，毕竟命令发送也是有一定的时间误差，芯片本身也是有一定的冗余。可以支持一定范围宽度的命令。

一般情况下，发送命令后，会有余震，会有回波。

当然这纯属理想情况。要知道在实际的应用中会有各种各样的状况发生。需要一一处理。尽量多的覆盖各种场景。

当然也可以根据捕获到的信号线上的命令进行诊断。后边再说。

回波判断

实际场景回波的数量一定不会只有一个。会有多有个脉冲，这时候就需要过滤出 有效的回波，可以在不同的距离上设置回波宽度门限，对干扰回波进行滤除。

余震判断

余震的长短可能会跟探头的批次有关。可以进行对空旷场景长时间的学习，得出余震的实际值，记录保存起来，便于在目标逐渐接近时，对障碍物是否进入盲区 做有效判断。

可以关注公众号，加入技术群，交流嵌入式的经验和知识。