0 引言
早些年在鹅厂实习了一段时间,因为没有什么特别紧急的需求(hahahahaha),所以主要花在了学习和捣鼓一些小工具上。有一个小需求是要实现鼠标拖动球体的转动,然后发现我不再能只用欧拉角来糊弄过去了。然后又发现,网上大部分资料的采用的欧拉角顺规都是xyz,然后我基于D3D11的辣鸡框架用了zxy,公式不太能直接套用,于是摸了两三天鱼,整理了一下几种三维旋转表示(欧拉角,四元数,旋转矩阵,轴角)与他们之间的相互转换的资料,并且加入了自己的一些推导,给出这些转换公式的推导思路和细节,这样子如果各位想使用其他欧拉角顺规和定义的时候,自己动手算一算就好了。
至于这几种三维旋转的表示形式随手百度Google都可以看到很多科普文的,这里着重说一下他们之间的转换的细节吧(不少公式和推导,预警一波,如果有错误请指出~)
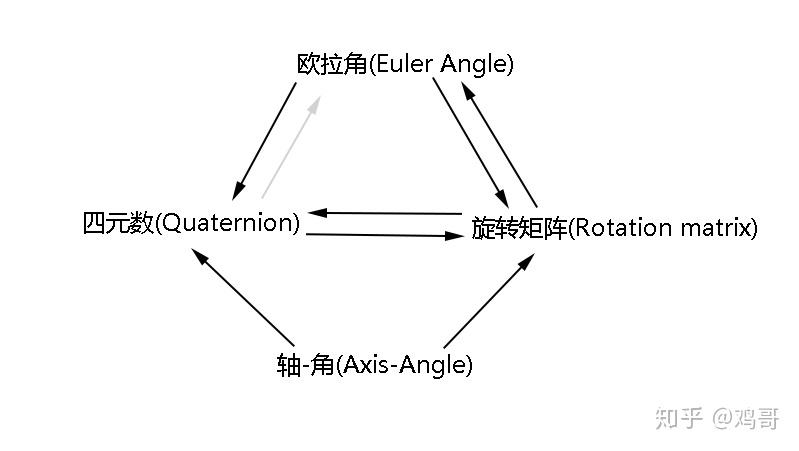
图:下文介绍的几种转换路径
1 欧拉角(Euler Angle)与旋转矩阵(Rotation Matrix)
1.1 欧拉角 ----> 旋转矩阵
D3D和OpenGL不同,用的坐标系是Y轴竖直向上的左手系,所以欧拉角的顺规是跟广大blog、OpenGL不一样的,那么博客上、甚至维基百科[2]上的各种基于右手系xyz顺规(分别对应roll, pitch,yaw)的看起来就不太能随随便便直接用了。
首先欧拉角旋转序列(Euler Angle Rotational Sequence)一共有12种顺规,6种绕三条轴的旋转(也叫Tait-Bryan Angle,XYZ,XZY,YXZ,YZX,ZXY,ZYX),另外6种只绕两条轴的旋转(也叫Proper Euler Angle,XYX,YXY,XZX,ZXZ,YZY,ZYZ)。如果相邻两次旋转是绕同一条轴,例如XXY,那么其实可以坍缩成XY。那么只绕一条轴旋转就根本不够自由度就不需要说了。也就是说,一共有12种基础旋转的组合顺序,它们可以旋转出三维的所有旋转状态。所以一共是12种旋转顺规(可以表示所有旋转的集合),DirectXMath库采用的是ZXY顺规,分别对应着Z-Roll,X-Pitch,Y-Yaw。
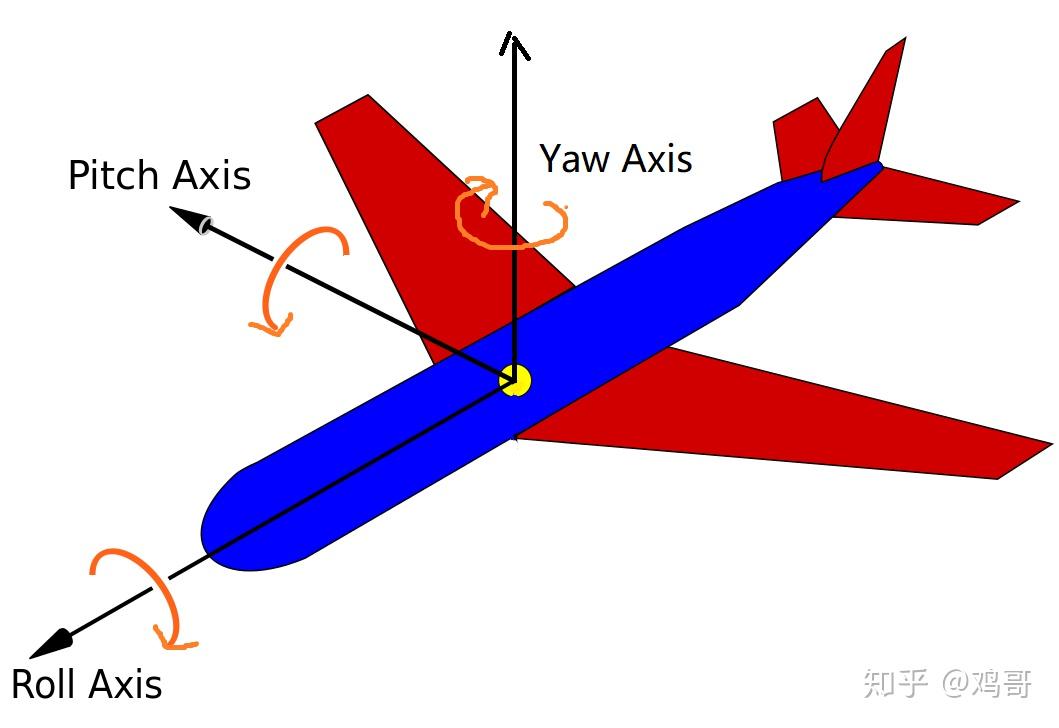
图:欧拉旋转与Yaw-Pitch-Roll的直观意义(网图魔改)
注意:那么下文我们都采用ZXY顺规来推导公式!采用列主向量(column major)!(但是注意DirectXMath API生成的矩阵其实是行主向量(row major)的)
参考一下维基百科的
[3]Euler Angle
Euler angles - Wikipediaen.wikipedia.org/wiki/Euler_angles编辑
[4]Rotation Matrix
Rotation matrix - Wikipediaen.wikipedia.org/wiki/Rotation_matrix编辑
欧拉角构造旋转矩阵就直接把三个Elemental Rotation Matrix乘在一起就好了(LaTeX扣得真累orz):
�(�,�,�)=��(�)��(�)��(�)=[����0����010−����0����][1000����−����0��������][����−����0��������0001]=[�10�1010−�10�1][1000�2−�20�2�2][�3−�30�3�30001]=[�1�1�2�1�20�2−�2−�1�1�2�1�2][�3−�30�3�30001]=[�1�3+�1�2�3�3�1�2−�1�3�2�1�2�3�2�3−�2�1�2�3−�1�3�1�3+�1�3�2�1�2]\begin{aligned} R(\alpha,\beta,\gamma) &=R_y (\alpha) R_x (\beta) R_z (\gamma) \\ &= \left[\begin{matrix} cos\alpha & 0 & sin\alpha \\ 0 & 1 & 0 \\ -sin\alpha & 0 & cos\alpha \end{matrix}\right] \left[\begin{matrix} 1 & 0 & 0 \\ 0 & cos\beta & -sin\beta \\ 0 & sin\beta & cos\beta \end{matrix}\right] \left[\begin{matrix} cos\gamma & -sin\gamma & 0 \\ sin\gamma & cos\gamma & 0 \\ 0 & 0 & 1 \end{matrix}\right] \\ &= \left[\begin{matrix} c_1 & 0 & s_1 \\ 0 & 1 & 0 \\ -s_1 & 0 & c_1 \end{matrix}\right] \left[\begin{matrix} 1 & 0 & 0 \\ 0 & c_2 & -s_2 \\ 0 & s_2 & c_2 \end{matrix}\right] \left[\begin{matrix} c_3 & -s_3 & 0 \\ s_3 & c_3 & 0 \\ 0 & 0 & 1 \end{matrix}\right] \\ &= \left[\begin{matrix} c_1 & s_1s_2 & s_1c_2 \\ 0 & c_2 & -s_2 \\ -s_1 & c_1s_2 & c_1c_2 \end{matrix}\right] \left[\begin{matrix} c_3 & -s_3 & 0 \\ s_3 & c_3 & 0 \\ 0 & 0 & 1 \end{matrix}\right] \\ &= \left[\begin{matrix} c_1c_3+s_1s_2s_3 & c_3s_1s_2-c_1s_3 & c_2s_1 \\ c_2s_3 & c_2c_3 & -s_2 \\ c_1s_2s_3-s_1c_3 & s_1s_3+c_1c_3s_2 & c_1c_2 \end{matrix}\right] \\ \end{aligned}
其中:
�1=���(�)=���(����),�1=����=���(����)�2=���(�)=���(�����ℎ),�2=����=���(�����ℎ)�3=���(�)=���(�����),�3=����=���(�����)c_1=cos(\alpha)=cos(Y_{yaw}), s_1=sin\alpha=sin(Y_{yaw})\\ c_2=cos(\beta)=cos(X_{pitch}), s_2=sin\beta=sin(X_{pitch})\\ c_3=cos(\gamma)=cos(Z_{roll}), s_3=sin\gamma=sin(Z_{roll})
这里要提一嘴内旋(intrinsic rotation)和外旋(extrinsic rotation):内旋的每个elemental绕的是object space basis的轴,外旋的每个elemental rotation绕的是world space(惯性系)basis的轴。上面的矩阵之所以是这么个顺序,是因为:
- 采用了ZXY顺规
- 采用列主向量
- 采用外旋的约定(毕竟在图形学里常用euler angle去表示物体相对于惯性系的旋转姿态)
那么给定一个向量 �v ,上面的矩阵左乘以这个向量,就是对它做一次主动旋转,得到变换后的向量 �′v' :
�′=��v'=Rv \\
在这规定下,上面的矩阵就是先roll Z,再pitch X,再yaw Y。
上面的欧拉角--->矩阵的结果与维基百科Euler Angles[3] �1�2�3Y_1X_2Z_3 给出的结果一致,那应该稳了:
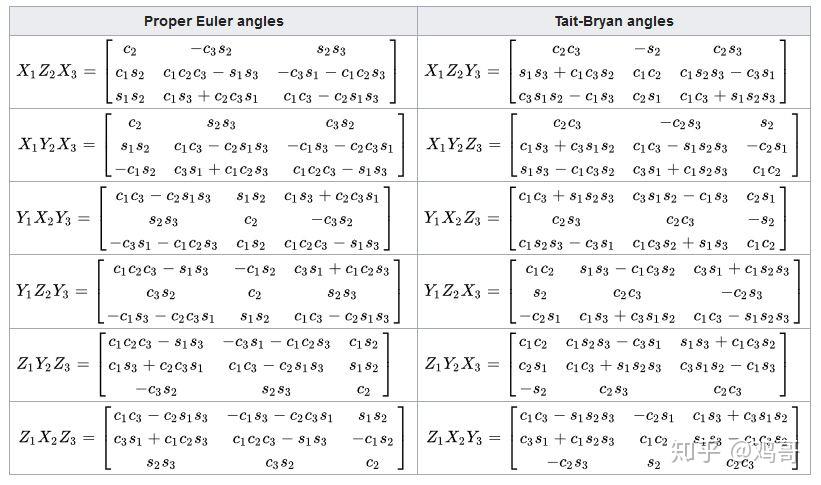
图:其实可以不用自己推的,维基百科把12种顺规乘出来的矩阵都写出来了
.
1.2 旋转矩阵----> 欧拉角
参考一篇NASA的关于姿态描述的技术报告[1]的Appendix-A6和[5],我们可以用旋转矩阵元素的相乘、相除、反三角函数等操作去“凑”出欧拉角。[5]给出了从XYZ顺规提取欧拉角的方法、步骤、思路,[1]则给出了全部12种顺规的欧拉角提取公式,但是没有给一些细节注意事项。所以总结一下,根据[1]、[5]、[7]《Real Time Rendering 3rd Edition》4.2.2和自己的推导,从ZXY顺规旋转矩阵提取欧拉角的公式是([1]原文下标似乎有点小问题):
- Y axis yaw angle:
�=����2(��������,��������)=����2(�13,�33)\alpha=atan2(sin\alpha cos\beta,cos\alpha cos\beta)=atan2(m_{13},m_{33})
- X axis pitch angle:
�=������(����)=������(−�23)\beta=arcsin(sin\beta)=arcsin(-m_{23})
- Z axis roll angle:
�=����2(��������,��������)=����2(�21,�22)\gamma=atan2(cos\beta sin\gamma,cos\beta cos\gamma)=atan2(m_{21},m_{22})
.
注意到一点,注意到矩阵的每一个元素都是pitch angle �\beta 的函数…所以当 �23=−����=±1m_{23}=-sin\beta=\pm1 即 ����=0cos\beta=0 的时候,这时候其他的欧拉角提取表达式就凉凉了(分子分母都是0, arctan和atan2都没有意义了)….其实pitch angle �=±�/2\beta=\pm \pi/2 恰好就是Gimbal Lock的位置。在Gimbal Lock的时候,旋转矩阵会退化为:
�(�,�,�)=[�1�3±�1�3±�3�1−�1�3000±1±�1�3−�1�3�1�3±�1�30]=[���(�±�)���(�±�)000±1−���(�±�)−���(�±�)0]\begin{aligned} R(\alpha,\beta,\gamma)&= \left[ \begin{matrix} c_1c_3\pm s_1s_3 & \pm c_3s_1-c_1s_3 & 0 \\ 0 & 0 & \pm 1 \\ \pm c_1s_3-s_1c_3 & s_1s_3 \pm c_1c_3 & 0 \end{matrix}\right]\\ &=\left[ \begin{matrix} cos(\alpha \pm \gamma) & sin(\alpha \pm \gamma) & 0 \\ 0 & 0 & \pm 1 \\ -sin(\alpha \pm \gamma) & -cos(\alpha \pm \gamma) & 0 \end{matrix}\right] \end{aligned}
.
那么要进一步处理万向节死锁的corner case就需要分两种情况:
- �=−�/2\beta=-\pi/2 ,此时 ����=−1,����=0 sin\beta=-1, cos\beta=0
�(�,�,�)=[�1�3−�1�3−�3�1−�1�3000±1−�1�3−�1�3�1�3−�1�30]=[���(�+�)−���(�+�)0001−���(�+�)−���(�+�)0]\begin{aligned} R(\alpha,\beta,\gamma)&= \left[ \begin{matrix} c_1c_3- s_1s_3 & -c_3s_1-c_1s_3 & 0 \\ 0 & 0 & \pm 1 \\ - c_1s_3-s_1c_3 & s_1s_3 - c_1c_3 & 0 \end{matrix}\right]\\ &=\left[ \begin{matrix} cos(\alpha + \gamma) & -sin(\alpha + \gamma) & 0 \\ 0 & 0 & 1 \\ -sin(\alpha + \gamma) & -cos(\alpha + \gamma) & 0 \end{matrix}\right] \end{aligned}
⇒�+�=����2(−�12,�11)\Rightarrow \alpha+\gamma =atan2(-m_{12},m_{11})
其中要给�\alpha或者 �\gamma其中一个欧拉角赋值,另外一个就按等式计算出来。
.
- �=�/2\beta=\pi/2 ,此时 ����=1,����=0 sin\beta=1, cos\beta=0
�(�,�,�)=[�1�3+�1�3�3�1−�1�3000−1�1�3−�1�3�1�3+�1�30]=[���(�−�)���(�−�)000−1−���(�−�)���(�−�)0]\begin{aligned} R(\alpha,\beta,\gamma)&= \left[ \begin{matrix} c_1c_3+ s_1s_3 & c_3s_1-c_1s_3 & 0 \\ 0 & 0 & -1 \\ c_1s_3-s_1c_3 & s_1s_3 + c_1c_3 & 0 \end{matrix}\right]\\ &=\left[ \begin{matrix} cos(\alpha - \gamma) & sin(\alpha - \gamma) & 0 \\ 0 & 0 & -1 \\ -sin(\alpha - \gamma) & cos(\alpha - \gamma) & 0 \end{matrix}\right] \end{aligned}
⇒�−�=����2(�12,�11)\Rightarrow \alpha - \gamma =atan2(m_{12},m_{11})
同样的,要给�\alpha或者 �\gamma其中一个欧拉角赋值,另外一个就按等式计算出来。
.
从旋转矩阵提取欧拉角的公式跟欧拉角顺规的选取有关,因为旋转矩阵的元素会略有不同,但是思路都是一样的,就是根据旋转矩阵的解析表达式+反三角函数凑出来23333。
2 四元数(Quaternion)与旋转矩阵
2.1 四元数---->旋转矩阵
众所周知的是,欧拉旋转是有万向节死锁(Gimbal Lock)的问题的。幸好我们有四元数(Quaternion)这种数学工具可以避免这个情况。一般来说,我们都会用单位四元数 q=�+�i+�j+�k\textbf q=w+x \textbf i+y \textbf j+z \textbf k 来表示旋转,其中 ||q||=�2+�2+�2+�2=1||\textbf q||=x^2+y^2+z^2+w^2=1 。那么给定一个单位四元数,可以构造旋转矩阵(column major)[1][4][8][14][15]:
�(�)=[1−2�2−2�22��−2��2��+2��2��+2��1−2�2−2�22��−2��2��−2��2��+2��1−2�2−2�2]\begin{aligned} R(q)&= \left[ \begin{matrix} 1-2y^2-2z^2 & 2xy-2zw & 2xz+2yw \\ 2xy+2zw & 1-2x^2-2z^2 & 2yz-2xw\\ 2xz-2yw & 2yz+2xw & 1-2x^2-2y^2 \end{matrix}\right]\\ \end{aligned}
这个四元数构造的大概思路就是把四元数的旋转操作写成矩阵形式(注:给定一个用于旋转的单位四元数 q=�+�i+�j+�k\textbf q=w+x \textbf i+y \textbf j+z \textbf k 和被旋转的三维向量 v\textbf v ,那么要直接用四元数旋转这个向量,则我们首先要构造一个纯四元数 p=(v,0)\textbf p=(\textbf v, 0) ,设旋转后的向量为 v′\textbf v' ,旋转后的向量构造的纯四元数为 p′=(v′,0)\textbf p'=(\textbf v', 0) ,那么 p′=qpq−1\textbf p'= \textbf q \textbf p \textbf q^-1 )。因为是用四元数来构造矩阵的,所以这个矩阵构造公式就没有欧拉角顺规的说法了。
.
2.2 旋转矩阵---->四元数
那第一步肯定是判断3x3矩阵是一个正交矩阵啦(满足 ���=���=�RR^T=R^TR=I )。那么如果这个矩阵已经是一个合法的旋转矩阵了,要从旋转矩阵里提取四元数,也是可以像提取欧拉角那样,用参数化过的矩阵的表达式凑出来。参考[8]《Real Time Rendering 3rd edition》Chapter4的思路,我们观察一下用四元数分量进行参数化的矩阵�(�)R(q) ,然后经过一顿操作,我们发现:
�32−�23=(2��+2��)−(2��−2��)=4���13−�31=(2��+2��)−(2��−2��)=4���21−�12=(2��+2��)−(2��−2��)=4��m_{32}-m_{23}=(2yz+2xw)-(2yz-2xw)=4xw\\ m_{13}-m_{31}=(2xz+2yw)-(2xz-2yw)=4yw\\ m_{21}-m_{12}=(2xy+2zw)-(2xy-2zw)=4zw
于是我们再凑出个实分量�w ,就可以把四元数四个分量都用矩阵元素表示出来了。于是我们又机智地发现了一个等式:
��(�(�))=�11+�22+�33=3−4(�2+�2+�2)=4(1−(�2+�2+�2))−1=4�2−1\begin{aligned} tr(R(q))&=m_{11}+m_{22}+m_{33}\\ &=3-4(x^2+y^2+z^2)\\ &=4(1-(x^2+y^2+z^2))-1\\ &=4w^2-1 \end{aligned}
其中 ��(�)tr(M) 是矩阵 �M 的迹(trace),也就是矩阵对角元素的和。因为这里用的是3x3矩阵,跟其他资料里面的表示有一点不同。所以我们可以把四元数的四个分量都用矩阵元素凑出来了:
�=(��(�)+12�=�32−�234��=�13−�314��=�21−�124�w=\frac{\sqrt{(tr(R)+1}}{2}\\ x=\frac{m_{32}-m_{23}}{4w}\\ y=\frac{m_{13}-m_{31}}{4w}\\ z=\frac{m_{21}-m_{12}}{4w}\\
有一点《Real Time Rendering》提到的, �w 绝对值比较小的时候,可能会出现数值不稳定的情况,那么想要数值稳定的话就得用一种不用除法的方式来凑,在这不展开了,可以看一下RTR 2333。
3 欧拉角与四元数
3.1 欧拉角---->四元数
首先提一下四元数的乘积:
p=�1+v1=�1+�1i+�1j+�1kq=�2+v2=�2+�2i+�2j+�2k\textbf p=w_1+\textbf v_1=w_1+x_1 \textbf i + y_1 \textbf j + z_1 \textbf k \\ \textbf q=w_2+\textbf v_2=w_2+x_2 \textbf i + y_2 \textbf j + z_2 \textbf k
⇒pq=�1�2−v1⋅v2+�2v1+�1v2+v1×v2=[�1�2+�1�2+�1�2−�1�2�1�2+�1�2+�1�2−�1�2�1�2+�1�2+�1�2−�1�2�1�2−�1�2−�1�2−�1�2]\begin{aligned} \Rightarrow \textbf p \textbf q &= w_1w_2 - \textbf v_1 \cdot \textbf v_2 + w_2 \textbf v_1+w_1\textbf v_2 + \textbf v_1\times \textbf v_2 \\ &= \left[\begin{matrix} x_1w_2+w_1x_2+y_1z_2-z_1y_2\\ y_1w_2+w_1y_2+z_1x_2-x_1z_2\\ z_1w_2 + w_1z_2 + x_1y_2-y_1x_2\\ w_1w_2-x_1x_2-y_1y_2-z_1z_2 \end{matrix}\right] \end{aligned}
参考维基百科[2]的思路,欧拉角构造四元数,跟欧拉角构造旋转矩阵一样,就是把三个基础旋转Elemental Rotation组合在一起。
那么用于旋转的四元数 �(�,�,�,�)q(x,y,z,w) 的表达式是:
�(�,�,�)=��(�)��(�)��(�)=[0����/20����/2][����/200����/2][00����/2����/2]=[���(�/2)���(�/2)���(�/2)���(�/2)−���(�/2)���(�/2)���(�/2)���(�/2)][00����/2����/2]=[���(�/2)���(�/2)���(�/2)+���(�/2)���(�/2)���(�/2)���(�/2)���(�/2)���(�/2)−���(�/2)���(�/2)���(�/2)−���(�/2)���(�/2)���(�/2)+���(�/2)���(�/2)���(�/2)���(�/2)���(�/2)���(�/2)+���(�/2)���(�/2)���(�/2)]\begin{aligned} q(\alpha,\beta,\gamma) &=q_y(\alpha)q_x(\beta)q_z(\gamma)\\ &=\left[ \begin{matrix} 0 \\sin\alpha/2\\0\\cos\alpha/2 \\ \end{matrix}\right] \left[ \begin{matrix} sin\beta/2 \\0\\0\\cos\beta/2 \\ \end{matrix}\right] \left[ \begin{matrix} 0 \\0\\sin\gamma/2\\cos\gamma/2 \\ \end{matrix}\right]\\ &=\left[ \begin{matrix} cos(\alpha/2)sin(\beta/2) \\sin(\alpha/2)cos(\beta/2)\\-sin(\alpha/2)sin(\beta/2)\\cos(\alpha/2)cos(\beta/2) \\ \end{matrix}\right] \left[ \begin{matrix} 0 \\0\\sin\gamma/2\\cos\gamma/2 \\ \end{matrix}\right] \\ &=\left[ \begin{matrix} cos(\alpha/2)sin(\beta/2)cos(\gamma/2)+sin(\alpha/2)cos(\beta/2)sin(\gamma/2) \\ sin(\alpha/2)cos(\beta/2)cos(\gamma/2)-cos(\alpha/2)sin(\beta/2)sin(\gamma/2)\\ -sin(\alpha/2)sin(\beta/2)cos(\gamma/2)+cos(\alpha/2)cos(\beta/2)sin(\gamma/2)\\ cos(\alpha/2)cos(\beta/2)cos(\gamma/2)+sin(\alpha/2)sin(\beta/2)sin(\gamma/2) \\ \end{matrix}\right] \end{aligned}
这个我自己推导的结果跟[1]NASA Technical Report的Appendix A给出的结果对比过了
([1]中四元数记号是 q=�1+�2i+�3j+�4k\textbf q=q_1+q_2 \textbf i + q_3 \textbf j + q_4 \textbf k ),看起来没什么问题。
.
3.2 四元数---->欧拉角
本来我以为,从四元数提取欧拉角的思路可以跟旋转矩阵提取欧拉角类似,也是用四元数的元素运算和反三角函数凑出公式来。后来我发现这简直就是一个极其硬核的任务,展开之后每一项都是六次多项式,画面有一丢暴力且少儿不宜,直接强行凑的话画风大概是这样:
��=(�1�2�3+�1�2�3)(�1�2�3+�1�2�3)=�12�2�2�32+�1�2�22�3�3+�1�1�22�3�3+�12�2�2�32��=(�1�2�3−�1�2�3)(−�1�2�3+�1�2�3)=−�12�2�2�32+�1�1�22�3�3+�1�1�22�3�3−�12�2�2�32\begin{aligned} xw&=(c_1s_2c_3+s_1c_2s_3)(c_1c_2c_3+s_1s_2s_3)\\ &=c_1^2c_2s_2c_3^2+c_1s_2s_2^2c_3s_3+c_1s_1c_2^2c_3s_3+s_1^2c_2s_2s_3^2 \end{aligned}\\ \begin{aligned} yz&=(s_1c_2c_3-c_1s_2s_3)(-s_1s_2c_3+c_1c_2s_3)\\ &=-s_1^2c_2s_2c_3^2+c_1s_1c_2^2c_3s_3+c_1s_1s_2^2c_3s_3-c_1^2c_2s_2s_3^2 \end{aligned}
⇒2(��−��)=2(�12�2�2+�12�2�2)=2�2�2=���� \Rightarrow 2(xw-yz)=2(c_1^2c_2s_2+s_1^2c_2s_2) =2c_2s_2 =sin\beta
⇒�=������(2(��−��))=������(−�23)\begin{aligned} \Rightarrow \beta = arcsin(2(xw-yz))=arcsin(-m_{23}) \end{aligned}
这个结果跟欧拉角参数化的旋转矩阵的 �23=−����=2��−2��m_{23}=-sin\beta=2yz-2xw 的表达式是吻合的。但这还只是最好凑的那一个,惹不起惹不起。所以舒服的思路还是四元数-->旋转矩阵-->欧拉角,想一步到位的话,把四元数分量参数化的旋转矩阵、欧拉角参数化的旋转矩阵结合在一起,参考下旋转矩阵转欧拉角的方法,替换下元素就完事了。这里就不把公式展开了,因为四元数直接转欧拉角 跟 旋转矩阵转欧拉角一样,依旧是要处理gimbal lock的corner case,还是那么麻烦,所以这里先鸽了23333
4 轴-角(Axis-Angle)
4.1 轴角---->四元数
轴-角(Axis-Angle)顾名思义就是绕某条单位轴旋转一定角度,从这个意义上看,它构造四元数是非常舒服的,毕竟直观的几何意义有一点点类似,绕单位轴 \textbf u 旋转 \theta 的四元数是:
\textbf q(w,\textbf v)=(cos\frac{\theta}{2},\textbf usin\frac{\theta}{2})
.
4.2 轴角---->旋转矩阵
Axis Angle转Rotation Matrix可以从[9]罗德里格斯旋转公式Rodrigues Rotation Formula开始推导。
设 \textbf v 是我们要旋转的单位向量,旋转轴为 \textbf k , \textbf v 绕 \textbf k 旋转角度 \theta ,那么旋转后的向量为:
\textbf v_{rot}=\textbf vcos\theta+(\textbf k \times \textbf v)sin\theta + \textbf k (\textbf k \cdot \textbf v)(1-cos\theta)
这个公式的推导思路是这样子的,我们先对向量 \textbf v 进行正交分解,分解成投影到旋转轴 \textbf k 的分量和垂直于 \textbf k 的分量:
\textbf v=\textbf v_\parallel+\textbf v_\bot
其中:
\textbf v_\parallel=(\textbf v \cdot \textbf k)\textbf k \\ \textbf v_\bot = - \textbf k \times(\textbf k \times \textbf v)
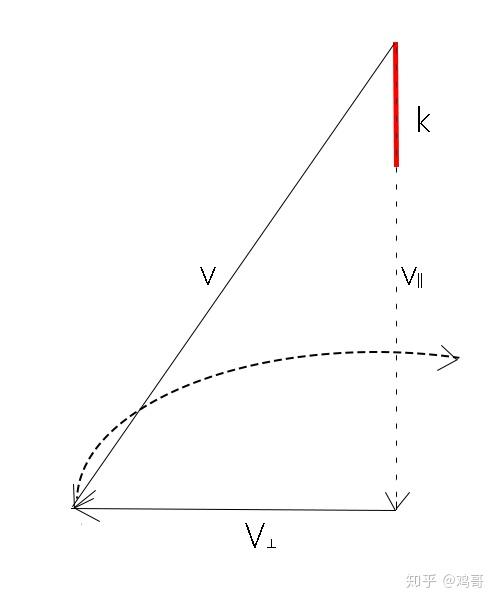
图:魔性p图,假设k和v都在屏幕这个平面上吧
于是绕 k\textbf k 旋转向量 v\textbf v 其实就是把上面正交投影后的向量分别旋转之后再加起来。那么很明显的,投影到旋转轴上的部分 v∥\textbf v_\parallel 都跟旋转轴共享了,那么自然旋转之后的结果就没有变化了,于是我们只需要旋转和旋转轴垂直的部分 v⊥\textbf v_\bot 。那么这个v⊥\textbf v_\bot旋转后的表达式就是:
v⊥−�������=����v⊥+����k×v \textbf v_{\bot -rotated}=cos\theta \textbf v_\bot +sin\theta \textbf k \times \textbf v
然后我们不按wikipedia里面坑爹的、不考虑下文的变形,自己推一波:
v�������=v⊥−�������+v∥−�������=����v⊥+����k×v+v∥=−����k×(k×v)+����k×v+(v−v⊥)=−����k×(k×v)+����k×v+(v−(−k×(k×v)))=v+(1−����)k×(k×v)+����k×v\begin{aligned} \textbf v_{rotated} &= \textbf v_{\bot-rotated}+\textbf v_{\parallel-rotated}\\ &=cos\theta \textbf v_\bot + sin\theta\textbf k \times \textbf v+\textbf v_\parallel \\ &=-cos\theta\textbf k \times (\textbf k\times \textbf v)+sin\theta\textbf k \times \textbf v+(\textbf v- \textbf v_\bot)\\ &=-cos\theta\textbf k \times (\textbf k\times \textbf v)+sin\theta\textbf k \times \textbf v+(\textbf v- (-\textbf k\times(\textbf k\times \textbf v)))\\ &=\textbf v+(1-cos\theta)\textbf k \times (\textbf k \times \textbf v) +sin\theta \textbf k \times \textbf v \end{aligned}
这里我们把旋转后向量的表达式变形得只剩下叉积(cross product),去掉点积(dot product)了,这样子我们才可以把这个绕轴旋转的表达式写成矩阵形式。怎么写呢?首先叉积可以写成矩阵形式:
M=[0−������0−��−����0]Mv=k×v\textbf M= \left[\begin{matrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x & 0 \\ \end{matrix}\right]\\ \textbf M\textbf v= \textbf k \times \textbf v
Cross product - Wikipediaen.wikipedia.org/wiki/Cross_product#Conversion_to_matrix_multiplication编辑
于是罗德里格斯旋转公式的变换就可以写成矩阵形式:
�(k,�)=I+����M+(1−����)M2R(\textbf k,\theta)=\textbf I +sin\theta \textbf M+(1-cos\theta)\textbf M^2
展开之后就是:
�(k,�)=[����+��2(1−����)−������+(1−����)����������+(1−����)����������+(1−����)��������+��2(1−����)−������+(1−����)����−������+(1−����)����������+(1−����)��������+��2(1−����)]R(\textbf k,\theta)=\left[ \begin{matrix} cos\theta + k_x^2(1-cos\theta) & -sin\theta k_z + (1-cos\theta)k_xk_y & sin\theta k_y+(1-cos\theta)k_xk_z\\ sin\theta k_z + (1-cos\theta)k_xk_y & cos\theta+k_y^2(1-cos\theta) & -sin\theta k_x +(1-cos\theta)k_yk_z \\ -sin\theta k_y + (1-cos\theta) k_xk_z & sin\theta k_x+(1-cos\theta)k_yk_z & cos\theta+ k_z^2(1-cos\theta) \end{matrix}\right]
罢工罢工!!LaTeX敲到我头皮发麻了!!
(不那么标准的)引用
[1]Henderson, D.M.. Euler angles, quaternions, and transformation matrices for space shuttle analysis[C]//NASA, Jun 09, 1977.
[3] https://en.wikipedia.org/wiki/Euler_angles
[4] https://en.wikipedia.org/wiki/Rotation_matrix
[5] Slabaugh G G. Computing Euler angles from a rotation matrix[J]. 1999.
[6] Mike Day, Converting a Rotation Matrix to a Quaternion. https://d3cw3dd2w32x2b.cloudfront.net/wp-content/uploads/2015/01/matrix-to-quat.pdf
[7] Tomas K.M. , Eric H., Naty H.. Real Time Rendering 3rd Edition , p68-p69, 2008.
[8] Tomas K.M. , Eric H., Naty H.. Real Time Rendering 3rd Edition , p76-p77, 2008.
[9] https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula
[10] https://en.wikipedia.org/wiki/Cross_product#Conversion_to_matrix_multiplication
[11] http://mathworld.wolfram.com/RodriguesRotationFormula.html
[12] https://zh.wikipedia.org/wiki/%E5%9B%9B%E5%85%83%E6%95%B8
[13] https://blog.csdn.net/silangquan/article/details/39008903
[14] Quaternion and Rotations, http://run.usc.edu/cs520-s12/quaternions/quaternions-cs520.pdf






















 2549
2549

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








