3D 基础：欧拉角、四元数、旋转矩阵、轴角

Introduction

关于各种数据表示格式的学习总结。

基础知识

欧拉角与旋转矩阵

欧拉角转换旋转矩阵

欧拉角旋转序列(Euler Angle Rotational Sequence)一共有12种顺规，6种绕三条轴的旋转(也叫Tait-Bryan Angle，XYZ,XZY,YXZ,YZX,ZXY,ZYX)，另外6种只绕两条轴的旋转(也叫Proper Euler Angle，XYX,YXY,XZX,ZXZ,YZY,ZYZ)。如果相邻两次旋转是绕同一条轴，例如XXY，那么其实可以坍缩成XY。那么只绕一条轴旋转就根本不够自由度就不需要说了。也就是说，一共有12种基础旋转的组合顺序，它们可以旋转出三维的所有旋转状态。所以一共是12种旋转顺规（可以表示所有旋转的集合），DirectXMath库采用的是ZXY顺规，分别对应着Z-Roll，X-Pitch，Y-Yaw。

欧拉角构造旋转矩阵就直接把三个Elemental Rotation Matrix乘在一起就好。
根据不同的转换顺序，可以计算出不同的公式。
https://en.wikipedia.org/wiki/Euler_angles 中给出了12种旋转顺序的公式。

万向锁

万向锁现象是欧拉角表征姿态的一个固有缺陷。
ZYX顺序旋转过程中，如果Y旋转是正负90度时，Y的旋转轴就变成了Z轴，相当于失去了一个自由度。

无论你怎么改变φ和ψ，你的旋转轴一直是Z轴不变。 导致自由度的缺失。
要想改变φ和ψ有不同的效果，你只能是去改变θ的值，以上就是用数学方法来解释为什么俯仰角在±90°时欧拉角出现万向锁的过程。
同一种空间状态欧拉角的表示方式不唯一，当出现万向锁现象时，同一种旋转有无数种欧拉角表示形式。
万向锁现象是欧拉角表征姿态的一个固有缺陷，所以，在进行姿态解算时往往会优先使用四元数方法进行描述。

旋转矩阵转换成欧拉角

通过上面的公式，可以计算出欧拉角。
但是：出现万向锁时候，旋转矩阵公式中的元素会产生简化。我们无法确定一个转角的具体值。

ZYX Euler Angles (roll, pitch, yaw)

Reference:
https://www.ccs.neu.edu/home/rplatt/cs5335_fall2016/slides/euler_quaternions.pdf

四元数

四元数是由1个实数加上3个复数组合而成，通常可以表示成w+xi+yj+zk或者（w,(x，y，z)）

为什么要用复数？

利用复数是为了把一个三维空间问题增加一个自由度，变成四维空间的问题。以下是一些重要的概念：
空间中的子空间：一般而言，空间（维度>2）都存在更低维的子空间，比如二维空间中一维子空间，也就是直线；三维空间中的一维子空间和二维子空间，也就是直线和面。高维空间中的平面我们称为超平面。

空间和子空间的映射：四维，(w,x,y,z)，当w=0时，(0,x,y,z)就是一个三维子空间，这也是为什么我们可以用单位四元数对三维向量进行操作，其实我们是将三维向量映射到四维的三维子空间（w=0，这种形式也成纯四元数），然后对其进行旋转，最终得到的向量结果依然是这个三维子空间中的，因而可以映射回三维空间。

广义球：我们在二维平面上，广义球其实指代circle，三维空间上就是我们认知上的球，称为two-sphere，而四维空间中广义球其实是一个超球（hyper-sphere），又称为three-sphere。单位向量其实就是广义球上面的点，而单位四元数也就是three-sphere上面的点。

约束与特征向量：对于空间的点加以约束，则该会减少参数的数量，比如三维空间的点在某一单位球面上，原本三个参数{x, y, z}才能表达的点现在只需要两个参数{u, v}就可以表达。如果{u, v}是单位向量，也可以称{u, v}是{x, y, z}的特征向量。

四元数与旋转

下面会解释一下利用复数是怎么把四元数与旋转联系起来。

上面的向量可以表示一个旋转，通过转换成极坐标的形式，通过欧拉公式的转换，可以得到下面的结果。

欧拉公式：

通过欧拉公式转换后的结果，可以转化为四元数。

四元数转换成旋转矩阵

已知一个代表旋转的单位四元数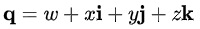
和一个被旋转的向量v：

1. 构造一个纯四元数 p =（v,0）,旋转之后变成p’ = （v’,0）
2. p’ = q p q ^(-1)

计算之后获得公式

四元数理解

四元数自由度并没有四个维度，由于存在w²+x²+y²+z²=1这个约束，它的自由度其实只有3。

上面小结中的第一部构建了一个纯四元数：
纯四元数(Pure Quaternion)，表示为{0, p}，就是w=0的四元数。其实上回已经分析过这个空间了，处于四维空间中w=0的三维子空间。
所以四元数旋转的过程可以理解为，构建一个纯四元数之后，在纯四元数这个三维子空间中进行旋转，再转换成一个旋转后的纯四元数。
四元数乘法：
四元数乘法和复数的矩阵乘法其实是等价的。



右边是z2的向量形式，左边是z1的矩阵形式。

p’ = q p q ^(-1) 解释

这个公式是四元数乘法的普适公式。

如果四元数中的w等于0, 旋转后的四元数仍然会在w=0下的三维空间。
w 不等于0，旋转后的四元数的w会变化，不会保持在同一个三维空间内。
这导致了旋转过程中的公式是不同的。
w 不等于0时，需要进行两次旋转，第一次旋转之后，w会变化，旋转之后处于不同的三维空间里面（q p）。第二次旋转之后，相当于转换回最初的w空间下的三维空间的坐标。这也是为什么乘上q ^(-1)的原因。
公式推导请见帖子：https://zhuanlan.zhihu.com/p/27541307

旋转矩阵转换成四元数

从旋转矩阵里提取四元数，也是可以像提取欧拉角那样，用参数化过的矩阵的表达式凑出来

四元数的优点

1.平滑插值：slerp和squad提供了方位间的平滑插值，没有其他方法能提供平滑插值。
2.快速连接和角位移求逆：四元数叉乘能将角位移序列转换为单个角位移，用矩阵做同样的操作明显会慢一些。
（四元数共轭提供了一种有效计算反角位移的方法，通过转置矩阵也能达到同样的目的，但不如四元数来得容易。）
3.(能和矩阵形式快速转换：四元数和矩阵的转换比欧拉角与矩阵之间的转换稍微快一些。)
4.(仅用四个数：四元数仅包含四个数，而矩阵用了9个数，它比矩阵“经济”得多（当然仍然比欧拉角多33%）。)

四元数缺点

1.比欧拉角空间稍微大一些。
2.四元数可能出现不合法现象：坏的输入数据或浮点数舍入误差累积都可能使四元数不合法（能通过四元数表转化解决这个问题，确保四元数为单位大小）。
3.难于使用。在所有三种方式中。四元数是最难于直接使用的。

四元数插值：球面（Slerp）插值

其实插值问题一直都算是图形学中比较经典的问题，一般来说线性插值可以满足大多数的情况，但是对于旋转来说，线性插值肯定效果不好，如下图

球面（Slerp）插值

球面插值的一般形式
主体思想其实就是施密特正交，先根据 q_a 和 q_b 解算出两个正交的四元数 q_0 和 q_1，然后通过加权算出最终的 q(t)。

接下来会证明：上面的一般向量形式可以转换转换成下面的四元数相乘格式。

1. 把下面的公式代入到上方的一般形式公式中。
   
   结果得到了q1^(t)，证明了一般形式与四元数乘法结果是相通的。

（Reference: https://zhuanlan.zhihu.com/p/28189289）

四元数应用：顺序无关的旋转混合

Reference: https://zhuanlan.zhihu.com/p/28330428

需要解决的问题

我们知道旋转操作所构成的空间非线性，无法对旋转操作直接进行线性叠加。表示旋转的四元数也不能直接简单的线性叠加，并且旋转操作具有不可交换性，交换后结果不同。

近似解：

如果不要求那么高的精度而只是找个看起来凑合的近似解的话，扩展一下对于两个四元数的NLerp操作（Normalized Lerp），直接对多个四元数进行线性叠加然后Normalize一下，在这些四元数所代表的旋转差别不大的情况下，效果也还可以。

“精确”的混合

困难点

• 对这些四元数依次相乘肯定是不行的，因为四元数乘法顺序相关；
• 用SLerp只能针对两个四元数进行“精确”的混合（这里“精确”指的是角速度匀速的球面插值），但是SLerp没法扩展到多个四元数

方案：
方案的注意点：下面的方法只适用于additive pose，它的内容是个变化量（位移，旋转）而不是位置量（位置，朝向）。
通过把多个旋转中的每个旋转都划分成n多份，在每一步旋转过程中，都进行多个小旋转。

证明过程请看原帖子/ Linear Combination of Transformations 2002 siggraph的论文。
应用：用在动画中，计算多个动作变化的插值模拟。
这个方法是对于旋转的，对于朝向的是另外的方法：如何平均一堆四元数所表示的朝向。

轴角和四元数的关系

轴-角(Axis-Angle)顾名思义就是绕某条单位轴旋转一定角度，从这个意义上看，它构造四元数是非常舒服的，毕竟直观的几何意义有一点点类似，绕单位轴u旋转 theta 的四元数是

总结

欧拉角：非常直观，我们可以很容易理解它的意思，也能想象出对应的空间位置，但是存在万向锁现象，导致后面有很多数学问题。

旋转矩阵：旋转矩阵有9个元素，计算繁杂，尤其是求微分时，而且也不直观。

四元数：没有奇点，能表征任何旋转关系，而且表示简单，只有四个元素，计算量小，但是不直观

选择哪种？

1.欧拉角最容易使用。当需要为世界中的物体制定方位时，欧拉角能大大简化人机交互，包括直接的键盘输入方位，在代码中指定方位（如为渲染设定摄像机）、在调试中测试。这个优点不应被忽视，不要以“优化”为名义而牺牲易用性，除非您确定这种优化的确有效果。
2.如果需要在坐标系之间转换位置，那么就选择矩阵形式。当然这并不意味着您就不能用其它格式来保存方位，并在需要的时候转换到矩阵格式。另一种方法是用欧拉角作为方位“主拷贝”但同时维护一个旋转矩阵，当欧拉角发生改变时矩阵也要同时进行更新。
3.当需要**大量保存方位数据（如动画）**时，就使用欧拉角或四元数。欧拉角蒋少占25%的内存，但它在转换到矩阵时要稍微慢一些。如果动画数据需要嵌套坐标系之间的连接，四元数可能使最好的选择。
4.**平滑的插值只能用四元数完成。**如果您用其它格式，也可以先转换到四元数然后再插值，插值完毕后再转换回原来的形式。

Reference

1: https://zhuanlan.zhihu.com/p/45404840
2: https://zhuanlan.zhihu.com/p/79894982
3. https://zhuanlan.zhihu.com/p/27471300
4. https://krasjet.github.io/quaternion/quaternion.pdf
5. https://blog.csdn.net/pizi0475/article/details/6261667
6. https://www.ccs.neu.edu/home/rplatt/cs5335_fall2016/slides/euler_quaternions.pdf