漫步线性代数十二——网络

上篇文章举的例子是$3\times 4$矩阵，从理论角度来说它解决了我们要求的问题：计算四个子空间以及他们的维数$r,n-r,r,m-r$都是非零的。但是这个例子并是不是由实际应用产生的，它没有说明这些子空间本质是什么。

本篇文章介绍一类长方形矩阵，他们有两个优点，简单和重要。他们就是图的相关矩阵，每个元素都是1，-1或0，值得注意的还有四个子空间的基向量是相同的，这些子空间在网络理论中地位非常重要，我们需要强调一下，这里的图可不是函数图(像$y=x^2$的抛物线图)，这里的图是与计算机科学相关的而不是微积分里面的图，这里的更加容易解释。这里我们将会看到在长方形矩阵上进行一些操作，最后神奇般的变成了对称矩阵$A^TA$。

图由点以及连接他们的边组成，图1中的图有4个点，5条边，在点1和4之间没有边(不允许自己连自己)，这个图是有向图，因为每条边上都有箭头。

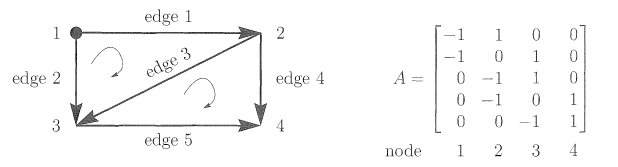
图1：有向图和它的相关矩阵

注意$A$的列，第3列给出了点3的信息——它告诉我们哪些边进来哪些边出去，边2 和3进，边5出。有时$A$也叫做连接矩阵或拓扑矩阵，当图有$m$条边$n$个点时，$A$是$m\times n$矩阵(通常情况下$m>n$)，它的转置是点边相关矩阵。

四个基本子空间在这个图里都有意义，我们将他们写成电压和电流的形式。

$A$的零空间：是否有一个列组合使得$Ax=0$？一般情况下这个答案需要先进行消元，但是这里能够立马看出来，所有列加起来等于一列零，零空间包含$x=(1,1,1,1)$，因为$Ax=0$， 方程$Ax=b$不存在唯一解(如果有解的话)，任何常向量$x=(c,c,c,c)$都能够加起来等于$Ax=b$的特解，完整解存在一个任意常数$c$(就像微积分中计算不定积分时候的$+C$)。

如果我们将$x_1,x_2,x_3,x_4$看做结点的电压，那就很有意义了，$Ax$的五个元素给出了五条边的电压差，从第一行可以得到边1的差为$x_2-x_1$。

对于方程$Ax=b$，给定差值$b_1,\ldots,b_5$，如何找出$x_1,\ldots,x_4$，但是这个无法做出来！我们可以加上常数$c$来提高或降低电压，差值是不会变得，因为$x=(c,c,c,c)$ 在$A$的零空间里。因为$Ax=0$意味着通过每条边的电压相等，碰巧这个矩阵的零空间是一维的，秩为$4-1=3$。

列空间：对于哪些$b_1,\ldots,b_5$，我们可以求解$Ax=b$呢？现在回到矩阵上，行1加行3等于行2，右边需要满足$b_1+b_3=b_2$或者无解，同样的，行3加行5等于行4，右边必须满足$b_3+b_5=b_4$，从消元的角度来说就是$0=0$。也就是说如果$b$在列空间里，那么

$$\begin{equation} b_1-b_2+b_3=0\quad and\quad b_3-b_4+b_5=0\tag1 \end{equation}$$

继续这个过程会发现行1加行4等于行2加行5，但是不会产生新东西；(1)中的方程相减就能得到$b_1+b_4=b_2+b_5$。因为列空间维数是5-2，所以这五个元素有两个条件，虽然这些条件是来自消元过程，但是在图里面他们都是有意义的。

基尔霍夫电压定理表明：沿着闭合回路上的电压差相加一定等于零，在图1上面环中，差值满足$(x_2-x_1)+(x_3-x_2)=(x_3-x_1)$，$b_1+b_3=b_2$，对于下面的闭环需要$b_3+b_5=b_4$。

18、对于$b$是否在列空间中，实际就是看是否符合基尔霍夫电压定理：闭环中电压差的和一定等于零。

左零空间：为了求解$A^Ty=0$，我们需要找出它在图中的意义，向量$y$有五个元素，分别代表每条边，这些数表示五条边上的电流。因为$A^T$是$4\times 5$，所以方程$A^Ty=0$对着五个电流有四个条件，他们就是每个结点的守恒约束：每个结点流入的电流等于流出的电流：

ATy=0−y1−y2y1−y3y2+y3y4−y4−y5+y5=0=0=0=0

$$A^Ty=0\quad \begin{array}{rcc} -y_1-y_2&&=0\\ y_1-y_3&-y_4&=0\\ y_2+y_3&-y_5&=0\\ y_4&+y_5&=0 \end{array}$$

这个网络理论的美妙之处就在于$A,A^T$发挥着重要的角色。

求解$A^Ty=0$意味着找到一组电流集合，使得它不会堆积到任何一个结点上，流动必须是循环的，最简单的解就是一个小闭环里的电流，我们图中有两个环，假设每个闭环里有1安培的电流：

$$y_1^T=\begin{bmatrix} 1&-1&1&0&0 \end{bmatrix} \quad y_2^T=\begin{bmatrix} 0&0&1&-1&1 \end{bmatrix}$$

每个闭环得到一个左零空间的向量$y$，元素$+1，-1$表示方向与箭头一致还是相反，$y_1,y_2$的所有组合充满了左零空间，所以$y_1,y_2$是一个基(维数肯定是$m-r=5-3=2$)。事实上$y_1-y_2=(1,-1,0,1,-1)$给出了图外围的大环。

列空间和左零空间关系比较紧密。左零空间包含$y_1=(1,-1,1,0,0)$，列空间满足$b_1+b_2+b_3=0$，那么$y^Tb=0$：列空间中的向量和左零空间中的向量是垂直的！

行空间：$A$的行空间包含$R^4$中的向量，但不是全部，它的维数是秩$r=3$，消元过程将找到三个无关行，并且我们也能从图中看出来。前三行是相关的(行1加行3等于行2，这些边形成一个环)，行1,2,4是无关的，因为边1,2,4无法形成环。

行1,2,4是行空间的基，每行元素加起来等于零，行空间的而所有组合$(f_1,f_2,f_3,f_4)$有下面的性质：

$$\begin{equation} f{\text{在行空间里}}:f_1+f_2+f_3+f_4=0\quad x{\text{在零空间里}}:x=c(1,1,1,1)\tag2 \end{equation}$$

这再次说明了基本定理：行空间垂直于零空间。如果$f$在行空间里，$x$在零空间里，那么$f^Tx=0$。

对于$A^T$，网络理论的基本定律是基尔霍夫电流定律：每个结点的总流量等于零。数$f_1,f_2,f_3,f_4$是结点的电流源，$f_1$必须平衡$-y_1-y_2$，也就是流出结点1的电流量。同其他三个结点同样如此，每秒的是$A^T$时电流定律的右矩阵。

19、结点方程$A^Ty=f$表示基尔霍夫电流定律：网络中结点的流量等于零，也就是流出等于流入。

这个定理在外围的总电流是$f_1+f_2+f_3+f_4=0$是才满足，也就是$f=0$，定律$A^Ty=0$是满足的。

生成树和无关行

左零空间中元素$y_1,y_2$是1或-1或0，零空间同样如此$x=(1,1,1,1)$，还有$PA=LDU$中的所有元素！关键点在于每个消元步骤在图中都是有意义的。

首先看矩阵$A$的第一步：行2减行1，我们可以用新边代替边2：消元步骤销毁了一条边，但产生了一条新边(图2)，这里新边仅仅和之前的边3方向相反。下一步消元将在第三行得到零，这说明行1,2,3是相关的，如果对应的边包含一个环那他们就是相关的。

消元的最后一步我们得到$r$个无关行，这$r$个边形成一棵树——一个无环图。图中$r=3$，边1,2,4组成一个可能的树，全名叫生成树，因为树生成了图的所有结点，如果图相连的话，生成树有$n-1$条边，在增加一条的话将产生回路。

图2

用线性代数的语言来说，$n-1$是矩阵$A$的秩，行空间的维数是$n-1$，从消元中得到的生成树给出了行空间的一个基——树中的每条边对应基中的一行。

线性代数的基本定理连系上了子空间的维数：

1. 零空间：维数为1，包含$x=(1,\ldots,1)$。
2. 列空间：维数为$r=n-1$，任何$n-1$列都是无关的。
3. 行空间：维数为$r=n-1$，从任意生成树中得到无关行。
4. 左零空间：维数为$m-r=m-n+1$，包含环中的$y$。

这四行给出了欧拉公式，是拓扑学的第一个定理，它计算了零维的结点数减去一维的边数加上二维的环数，对任何连接图都有一个线性代数的证明：

$$\begin{equation} \text{结点数}+\text{边数}+\text{环数}=(n)-(m)+(m-n+1)=1\tag3 \end{equation}$$

对于10个结点10条边的单环，欧拉数为10-10=1，如果这10个结点都连接到中心的第11个点，那么11-20+10依然是1。

行空间中的每个向量$f$满足$x^Tf=f_1+\cdots+f_n=0$——外围的电流等于零，列空间中的每个向量满足$y^Tb=0$——所有环的电压差加起来等于零，等会用欧姆定律将$x,y$联系起来。

网络

当给边分配数值$c_1,\ldots,c_m$时，图就变成了网络，数$c_i$可以是边$i$的长度，也可以是容量，也可以是硬度或电导率等。这些数放到$4\times 4$的对角矩阵$C$中，$C$反映了物质属性，相比较矩阵$A$，它给出了连接信息。

我们这里用电导率进行描述，在边$i$上，电导率是$c_i$，电阻是$1/c_i$，欧姆定律表明流经电阻的电流$y_i$和压降$e_i$成比例：

$$y_i=1/c_ie_i$$

也可以写成$E=IR$，压降等于电流乘以电阻。一次考虑一个方程，那么欧姆定律就是$y=Ce$。

我们需要基尔霍夫电压定律和电流定律来完成整个框架：

• KVL：每个环中的压降加起来等于零。
• KCL：每个结点的电流$y_i$加起来的零。

电压定律允许我们给每个结点分配势能$x_1,\ldots,x_n$，那么一个环中的电压差就类似于$(x_2-x_1)+(x_3-x_2)+(x_1-x_3)=0$。电流定律告诉我们将结点的电流加起来，用矩阵表示就是$A^Ty$，如果没有额外的电流源，根据基尔霍夫定律可得$A^Ty=0$。

另一个方程是欧姆定律，但是我们需要找出通过电阻的压降。$Ax$给出了结点的压差，反转一下符号，$-Ax$给出了压降。降的部分是因为每条边上的电池强度$b_i$，其余部分是通过电阻的$e=b-Ax$：

$$\begin{equation} y=C(b-Ax)\quad or\quad C^{-1}y+Ax=b\tag4 \end{equation}$$

基本平衡方程结合了欧姆定律和基尔霍夫定律，它是应用数学的中心问题，这些方程几乎出现在任何地方：

$$\begin{equation} \begin{array}{ccccc} C^{-1}y&+&Ax&=&b\\ A^Ty&&&=&f \end{array}\tag5 \end{equation}$$

这是一个线性对称系统，未知量是电流$y$和电压$x$，用矩阵的形式表示就是：

$$\begin{equation} \begin{bmatrix} C^{-1}&A\\A^T&0 \end{bmatrix} \begin{bmatrix} y\\x \end{bmatrix}= \begin{bmatrix} b\\f \end{bmatrix}\tag6 \end{equation}$$

对于块消元法，主元就是$C^{-1}$，乘数因子就是$A^TC$，执行消元得到：

$$\begin{bmatrix} C^{-1}&A\\0&-A^TCA \end{bmatrix} \begin{bmatrix} y\\x \end{bmatrix}= \begin{bmatrix} b\\f-A^TCb \end{bmatrix}$$

最后一行的方程只包含$x$：

$$\begin{equation} A^TCAx=A^TCb-f\tag7 \end{equation}$$

将其回代到第一个方程得到$y$。

注意：势能必须提前确定：$x_n=0$。第$n$个结点是接地的，所以原始矩阵的第$n$列会被移除，而在结果矩阵中它的$n-1$列是无关的，方阵$A^TCA$是$n-1$阶的可逆矩阵：

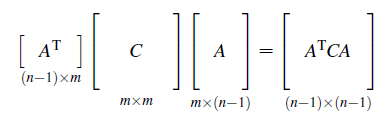
例1：假设电池 $b_3$和电流源 $f_2$ 连接四个结点，点4接地，势能固定为 $x_4=0$。第一件事是利是结点1,2,3电流定律 $A^Ty=0$：


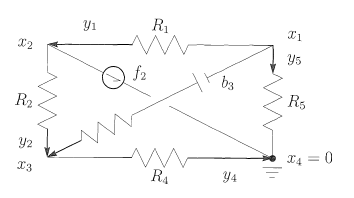
图3

$$\begin{matrix} -y_1&-&y_3&-&y_5&=&0\\ y_1&-&y_2&&&=&f_2\\ y_2&+&y_3&-&y_4&=&0 \end{matrix} \quad A^T= \begin{bmatrix} -1&0&-1&0&-1\\ 1&-1&0&0&0\\ 0&1&1&-1&0 \end{bmatrix}$$

结点4的方程没有写出来，根据电流定律方程为$y_4+y_5+f_2=0$，它可以由其余三个方程得到。

另一个方程是$C^{-1}y+Ay=b$，势能$x$根据欧姆定律与电流$y$连系起来，对角矩阵$C$包含五个电导率$c_i=1/R_i$，右边包含一个电池的电量$b_3$，块的表达形式为$C^{-1}y+Ax=b$：

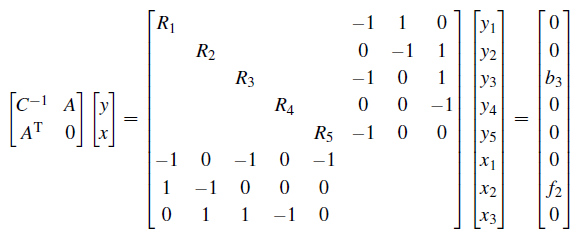
这个系统是 $8\times 8$的，有五个电流和三个势能， $y$的消元简化为$3\times 3$的系统 $A^TCAx=A^TCb-f$，矩阵 $A^TCA$包含 $c_i=1/R_i$，我们也给出了接地结点的行和列：


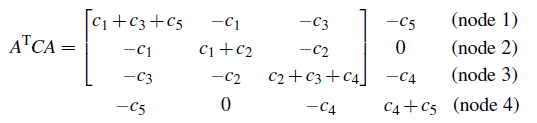
第一项是1+1+1或 $c_1+c_3+c_5$，因为边1,3,5连接点1，下一个对角项是1+1或 $c_1+c_2$，这些边连接点2，对角线外的 $c$ 都有个符号，接地结点4的边在第四行和第四列，为了使$A^TCA$可逆，所以将它去掉。

注意$A^TCA$是对称的，它的主元为正，来自于应用数学的基本框架，如图4所示：

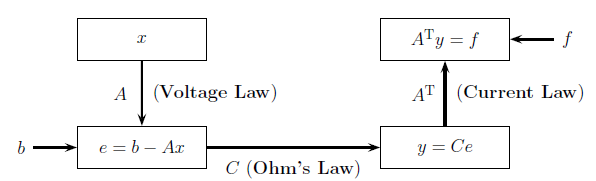
图4

在力学中，$x,y$表示位移和力。在流体中，未知量表示压力和流速。在统计学中，$e$是误差，$x$是最佳最小二乘拟合。

对于应用数学的基本问题，除了知道问题的解以外，我们需要看到更多的东西，我们最开始求解线性方程，然后进一步建立所需的方程，数学和人类的贡献不在于计算而在于思考。