线性代数与图与网络

incidence matrix（关联矩阵）

考虑如下的图：

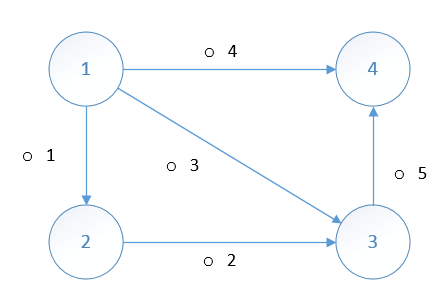
共四个节点（notes），五条边（edges），不妨赋予其一定的物理意义，如结点上的数值表示结点电势（potential），边即表示结点间的电势差（difference of potential）。
则可将该图转换为矩阵（关联矩阵）形式，矩阵的每一行表示一条边，每一列表示每一个结点，则矩阵的shape为 $5\times 4$：
$$A=\begin{bmatrix} -1,&1,&0,&0\\ 0,&-1,&1,&0\\ -1,&0,&1,&0\\ -1,&0,&0,&1\\ 0,&0,&-1,&1 \end{bmatrix}$$

我们看到结点1,2,3（1⇒ 2⇒ 3，与1⇒ 3）以及结点1,3,4（1⇒ 3⇒ 4，与1⇒ 4）均形成闭合回路（loop），loop对应于矩阵 $A$的含义即是，三条边线性相关（同理，线性无关表示没有回路），也即$A[1,:]+A[2,:]=A[3,:],\;A[3,:]+A[5,:]=A[4,:]$。

继续考察 $A$的零空间，也即 $Ax=0,\;x=[x_1,x_2,x_3,x_4]^T$，最终也即，$c[1,1,1,1]^T$构成零空间的一个基，零空间的维数为 $\dim N(A)=1$，则由 $\dim N(A)=n-rank(A)$，可知 $rank(A)=4-1=3$，据此可知 $A^T$ 的零空间 $\{y|A^Ty=0\}$，此时的 $\dim N(A^T)=m-rank(A)=5-3=2$。

$$A^Ty=0\\ \begin{bmatrix} -1,&0,&-1,&-1,&0\\ 1,&-1,&0,&0,&0\\ 0,&1,&1,&0,&-1\\ 0,&0,&0,&1,&1 \end{bmatrix}\cdot \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4\\ y_5 \end{bmatrix}=0$$
我们将 $y_1,y_2,y_3,y_4,y_5$ 分别定义为各自边上的电势差， $A^Ty=0$ 正是大名鼎鼎的 基尔霍夫定理（Kirchhoff’s circuit laws ，KCL）（某种意义上的守恒定理），写成方程组的形式为：
$$\begin{split} \left \{ \begin{array}{l} -y_1-y_3-y_4=0\\ y_1-y_2=0\\ y_2+y_3-y_5=0\\ y_4+y_5=0 \end{array} \right. \end{split}$$

我们可以清晰地看出，所谓的KCL（守恒定理）表示的是每一个结点的流入电流等于流出电流（电流在电路中流动，对每一个结点又不累积电荷）。
此时我们考虑 $N(A^T)$的一组基，其维数为2，则该组基中包含两个基向量，分别考虑两个环路（1⇒ 2⇒ 3⇐ 1，与1⇒ 3⇒ 4⇐ 1），也即：

$$\begin{bmatrix} 1\\ 1\\ -1\\ 0\\ 0\\ \end{bmatrix}, \begin{bmatrix} 0\\ 0\\ 1\\ -1\\ 1\\ \end{bmatrix}$$

如果考虑整个大的回路则得：

$$\begin{bmatrix} 1\\ 1\\ 0\\ -1\\ 1\\ \end{bmatrix}$$

在图理论中，没有环路的图称为树。

也即 $rank(A)=3$，消除环路之后的图（此时为树）为：

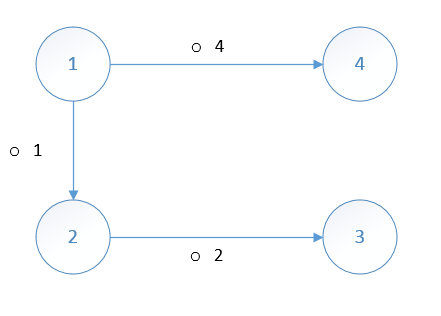
再来考察我们的维度公式：

$$\dim N(A^T)=m-rank(A)=m-(n-1)$$

放在这里的含义即为， $\#$ nodes - $\#$ edges+$\#$ loops=1 （这也就是著名的欧拉公式，也即我们用线性代数证明了欧拉公式，欧拉公式是任何图中都具有的拓扑性质）

$$e=Ax\\ y=Ce\\ f=A^Ty \Rightarrow f=A^TCAx$$