漫步线性代数十八——正交基和格拉姆-施密特正交化(下)

最新推荐文章于 2025-03-08 10:09:25 发布

会敲键盘的猩猩

最新推荐文章于 2025-03-08 10:09:25 发布

阅读量6.5k

点赞数 4

分类专栏：漫步线性代数文章标签：格拉姆-施密特傅里叶级数 QR分解

漫步线性代数专栏收录该内容

27 篇文章

订阅专栏

本文介绍了格拉姆-施密特正交化过程及其在向量空间和函数空间的应用，包括如何从一组线性无关的向量出发获得一组正交向量，以及如何将该方法应用于函数，生成正交多项式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

格拉姆-施密特

声明：以后博主会把文章的pdf版本陆续发布到的网上，免费供大家下载
正交基和格拉姆-施密特正交化

假设我们有是是三个无关向量 $a,b,c$ ，如果他们是正交的，那么会多问题都变得容易了。例如要计算 $v$ 到第一个向量的投影，只需计算 $(a^Tv)a$ ，投影到前两个向量所在的平面只需相加即可 $(a^Tv)a+(b^Tv)b$ ，同样投影到三个向量组成的空间就是三个投影相加，所有这些运算只需要计算内积 $a^Tv,b^Tv,c^Tv$ 。但是不要忘记有个大前提：向量正交，所以接下来我们就找出令向量正交的方法。

其实方法很简单，也就是给定 $a,b,c$ 得出我们需要的 $q_1,q_2,q_3$ 。对于 $q_1$ ：方向和 $a$ 一致，只需除以它的长度即可，这样的话 $a/\Vert a\Vert$ 就是单位向量。真正的计算要从 $q_2$ 开始，我们需要令它和 $q_1$ 正交，如果第二个向量 $b$ 存在 $q_1$ 方向(也就是 $a$ 的方向)的分量，那么我们需要减去这个分量：

B = b - (q T 1 b) q 1, q 2 = B / ∥ B ∥ (1)

$\begin{equation} B=b-(q_1^Tb)q_1,\quad q_2=B/\Vert B\Vert\tag1 \end{equation}$

$B$ 和 $q_1$ 是正交的，它是 $b$ 的一部分，但这部分不在 $a$ 上。图1中 $B$ 和 $q_1$ 正交，我们将它的方向设置成 $q_2$ 的方向。

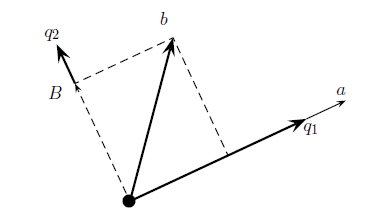
图1

$q_1,q_2$ 得到后，接下来寻找第三个正交方向，它肯定不在 $q_1,q_2$ 所在的平面上，也就是 $a,b$ 所在的平面。当然，可能有分量在这个平面上，这时候就必须将它减掉，(如果结果是 $C=0$ ，这就表示 $a,b,c$ 是相关的)留下的部分就是我们要的 $C$ ，这部分所在的方向垂直于 $q_1,q_2$ 所在的平面：

C = c - (q T 1 c) q 1 - (q T 2 c) q 2, q 3 = C / ∥ C ∥ (2)

$\begin{equation} C=c-(q_1^Tc)q_1-(q_2^Tc)q_2,\quad q_3=C/\Vert C\Vert\tag2 \end{equation}$

这就是格拉姆-施密特正交化的思想，先定一个向量，然后每增加一个向量，计算它是否有分量位于所定好的方向中，有的话就减去，没有的话直接加进去。对于上面的例子，如果有第四个向量的话，我们需要减去它在 $q_1,q_2,q_3$ 中的分量。

例5：假设 $a,b,c$ 是无关向量：

a = ⎡ ⎣ ⎢ 101 ⎤ ⎦ ⎥, b = ⎡ ⎣ ⎢ 100 ⎤ ⎦ ⎥, c = ⎡ ⎣ ⎢ 210 ⎤ ⎦ ⎥

$a=\begin{bmatrix} 1\\0\\1 \end{bmatrix},\quad b=\begin{bmatrix} 1\\0\\0 \end{bmatrix},\quad c=\begin{bmatrix} 2\\1\\0 \end{bmatrix}$

首先找 $q_1$ ，我们直接将第一个向量变成单位向量： $q_1=a/\sqrt{2}$ ，然后找 $q_2$ ，第二个向量减去它在第一个方向上的分量：

B = b - (q T 1 b) q 1 = ⎡ ⎣ ⎢ 100 ⎤ ⎦ ⎥ - 1 2 \sqrt ⎡ ⎣ ⎢ 1 / 2 \sqrt 0 1 / 2 \sqrt ⎤ ⎦ ⎥ = 1 2 ⎡ ⎣ ⎢ 10 - 1 ⎤ ⎦ ⎥

$B=b-(q_1^Tb)q_1=\begin{bmatrix} 1\\0\\0 \end{bmatrix} -\frac{1}{\sqrt{2}}\begin{bmatrix} 1/\sqrt{2}\\0\\1/\sqrt{2} \end{bmatrix} =\frac{1}{2} \begin{bmatrix} 1\\0\\-1 \end{bmatrix}$

然后 $B$ 除以它的长度得到归一化的 $q_2$ ：

⎡ ⎣ ⎢ 1 / 2 \sqrt 0 - 1 / 2 \sqrt ⎤ ⎦ ⎥

$\begin{bmatrix} 1/\sqrt{2}\\0\\-1/\sqrt{2} \end{bmatrix}$

接下来是 $q_3$ ，从 $c$ 中减去在 $q_1,q_2$ 上的分量：

C = c - (q T 1 c) q 1 - (q T 2 c) q 2 = ⎡ ⎣ ⎢ 210 ⎤ ⎦ ⎥ - 2 \sqrt ⎡ ⎣ ⎢ 1 / 2 \sqrt 0 1 / 2 \sqrt ⎤ ⎦ ⎥ - 2 \sqrt ⎡ ⎣ ⎢ 1 / 2 \sqrt 0 - 1 / 2 \sqrt ⎤ ⎦ ⎥ = ⎡ ⎣ ⎢ 010 ⎤ ⎦ ⎥

$\begin{align*} C&=c-(q_1^Tc)q_1-(q_2^Tc)q_2\\ &=\begin{bmatrix} 2\\1\\0 \end{bmatrix} -\sqrt{2} \begin{bmatrix} 1/\sqrt{2}\\0\\1/\sqrt{2} \end{bmatrix} -\sqrt{2} \begin{bmatrix} 1/\sqrt{2}\\0\\-1/\sqrt{2} \end{bmatrix} =\begin{bmatrix} 0\\1\\0 \end{bmatrix} \end{align*}$

可以看出它已经是单位向量，所以就是 $q_3$ ，至此得出一组正交向量 $q_1,q_2,q_3$ ，我们将它作为正交矩阵 $Q$ 的列：

Q = ⎡ ⎣ ⎢ q 1 q 2 q 3 ⎤ ⎦ ⎥ = ⎡ ⎣ ⎢ 1 / 2 \sqrt 0 1 / 2 \sqrt 1 / 2 \sqrt 0 - 1 / 2 \sqrt 010 ⎤ ⎦ ⎥

$Q=\begin{bmatrix} \\ q_1&q_2&q_3\\ \\ \end{bmatrix} =\begin{bmatrix} 1/\sqrt{2}&1/\sqrt{2}&0\\ 0&0&1\\ 1/\sqrt{2}&-1/\sqrt{2}&0\\ \end{bmatrix}$

20、格拉姆-施密特过程是无关向量 $a_1,\ldots,a_n$ 开始，最后得出正交向量 $q_1,\ldots,q_n$ 。在第 $j$ 步，我们用 $a_j$ 减去它在 $q_1,\ldots,q_{j-1}$ 方向上的分量：

A j = a j - (q T 1 a j) q 1 - \dots - (q T j - 1 a j) q j - 1 (3)

$\begin{equation} A_j=a_j-(q_1^Ta_j)q_1-\cdots-(q_{j-1}^Ta_j)q_{j-1}\tag3 \end{equation}$ 然后 $A_j/\Vert A_j\Vert$ 得到单位向量 $q_j$ 。

计算注解：下面的计算方法会更加容易：计算 $a,B,C$ 的时候先不归一化，等到全部计算出来后统一除以他们的长度。我们还以上面的情况为例，注意我们要用 $a^Tb/a^Ta$ 得到的 $\frac{1}{2}$ 而不是 $q^Tb$ 得到的 $\frac{1}{\sqrt{2}}$ ：

B = ⎡ ⎣ ⎢ 100 ⎤ ⎦ ⎥ - 1 2 ⎡ ⎣ ⎢ 101 ⎤ ⎦ ⎥, C = ⎡ ⎣ ⎢ 210 ⎤ ⎦ ⎥ - ⎡ ⎣ ⎢ 101 ⎤ ⎦ ⎥ - 2 ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ 1 2 0 - 1 2 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥

$B=\begin{bmatrix} 1\\0\\0 \end{bmatrix} -\frac{1}{2} \begin{bmatrix} 1\\0\\1 \end{bmatrix} ,\quad C=\begin{bmatrix} 2\\1\\0 \end{bmatrix} -\begin{bmatrix} 1\\0\\1 \end{bmatrix} -2\begin{bmatrix} \frac{1}{2}\\0\\-\frac{1}{2} \end{bmatrix}$

QR分解

我们从矩阵 $A$ 开始，它的列分别是 $a,b,c$ ，最后以矩阵 $Q$ 结束，它的列是 $q_1,q_2,q_3$ ，这些矩阵之间的关系是什么？当 $n$ 个向量都在 $m$ 为空间时， $A,Q$ 都是 $m\times n$ 矩阵，并且存在第三个矩阵将他们联系起来。

一个想法是将 $a$ 作为 $q$ 的组合，图1中的向量 $b$ 是正交向量 $q_1,q_2$ 的一个组合，并且我们还知道它的组合为：

b = (q T 1 b) q 1 + (q T 2 b) q 2

$b=(q_1^Tb)q_1+(q_2^Tb)q_2$

平面中的每个向量都是 $q_1,q_2$ 分量的和，同样的， $c$ 是 $q_1,q_2,q_3$ 分量的和： $c=(q_1^Tb)q_1+(q_2^Tb)q_2+(q_3^Tc)q_3$ ，如果我们用矩阵的形式来表示就得到 $A=QR$ ：

A = ⎡ ⎣ ⎢ a b c ⎤ ⎦ ⎥ = ⎡ ⎣ ⎢ q 1 q 2 q 3 ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ ⎢ q T 1 a q T 1 b q T 2 b q T 1 c q T 2 c q T 3 c ⎤ ⎦ ⎥ ⎥ = Q R (4)

$\begin{equation} A=\begin{bmatrix} \\ a&b&c\\ \\ \end{bmatrix} =\begin{bmatrix} \\ q_1&q_2&q_3\\ \\ \end{bmatrix} \begin{bmatrix} q_1^Ta&q_1^Tb&q_1^Tc\\ &q_2^Tb&q_2^Tc\\ &&q_3^Tc \end{bmatrix} =QR\tag4 \end{equation}$

注意最后那个矩阵中的零！ $R$ 是上三角矩阵，这当然与格拉姆-施密特的过程有关。第一个向量 $a,q_1$ 在同一条线上，然后 $q_1,q_2$ 和 $a,b$ 在同一个平面上。

$QR$ 分解就像 $A=LU$ ，不同的是第一个分解中的 $Q$ 的列是标准正交的，对于第二个因子，因为对角线的右边是非零值所以叫 $R$ 。将上例的具体数值代入的

A = ⎡ ⎣ ⎢ 101100210 ⎤ ⎦ ⎥ = ⎡ ⎣ ⎢ 1 / 2 \sqrt 0 1 / 2 \sqrt 1 / 2 \sqrt 0 - 1 / 2 \sqrt 010 ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ 2 \sqrt 1 / 2 \sqrt 1 / 2 \sqrt 2 \sqrt 2 \sqrt 1 ⎤ ⎦ ⎥ = Q R

$A=\begin{bmatrix} 1&1&2\\0&0&1\\1&0&0 \end{bmatrix} =\begin{bmatrix} 1/\sqrt{2}&1/\sqrt{2}&0\\ 0&0&1\\ 1/\sqrt{2}&-1/\sqrt{2}&0 \end{bmatrix} \begin{bmatrix} \sqrt{2}&1/\sqrt{2}&\sqrt{2}\\ &1/\sqrt{2}&\sqrt{2}\\ &&1 \end{bmatrix}=QR$

我们可以看到 $a,B,C$ 的长度位于 $R$ 的对角线上，标准正交向量 $q_1,q_2,q_3$ 都在 $Q$ 中。

可能 $QR$ 的形式没有 $LU$ 那样好看(由于有平方根)，但这两种方法在线性代数的理论中都是非常重要的，绝对处于中心地位。

我们用 $\Vert A_j\Vert q$ 代替(11)中的 $A_j$ 得：

a j = (q T 1 a j) q 1 + \dots + (q T j - 1 a j) q j - 1 + ∥ A j ∥ q j = Q \cdot R 的 第 j 列 (5)

$\begin{equation} a_j=(q_1^Ta_j)q_1+\cdots+(q_{j-1}^Ta_j)q_{j-1}+\Vert A_j\Vert q_j=Q\cdot R\text{的第$j$列}\tag5 \end{equation}$

21、每个含有无关列的 $m\times n$ 矩阵都能分解成 $A=QR$ 的形式， $Q$ 的列是标准正交的， $R$ 是上三角矩阵并且可逆。当 $m=n$ 时，所有的矩阵都是方阵， $Q$ 就变成正交矩阵。

我们不能忘记正交的是用来做什么的，它的目的是为了简化最小二乘问题 $Ax=b$ 。它对正规方程依然有用，只是 $A^TA$ 变得更简单了：

A T A = R T Q T Q R = R T R (6)

$\begin{equation} A^TA=R^TQ^TQR=R^TR\tag6 \end{equation}$

基本方程 $A^TA\hat{x}=A^Tb$ 简化为：

$R T R x^= R T Q T b 或者 R x^= Q T b (7)$ $\begin{equation} R^TR\hat{x}=R^TQ^Tb\quad \text{或者}\quad R\hat{x}=Q^Tb\tag7 \end{equation}$

我们不是求解 $QR=b$ ，况且它也无解，而是求解 $R\hat{x}=Q^Tb$ ，由于 $R$ 是三角矩阵，所以我们直接进行回代即可，实际代价是 $mn^2$ 次操作。

我们把同样的想法应用到函数上，正弦和余弦是正交的；幂 $1,x,x^2$ 不正交。当 $f(x)$ 写成正弦和余弦的组合式，得到的就是傅里叶级数，每一项都是在直线上的投影——函数空间中直线包含正弦和余弦的倍数 $\cos nx,\sin nx$ ，这和向量的情况完全是平行的，同样非常重要，最后提一下施密特的一个工作：正交化 $x$ 的幂，产生勒让德多项式。

函数空间和傅里叶级数

这部分主要内容有：

介绍最出名的无限维向量空间(希尔伯特空间)；

将长度和内积的想法从向量 $v$ 扩展到函数 $f(x)$ ；
认识到傅里叶级数是一维投影(正交列是正弦和余弦)的和；
在多项式 $1,x,x^2,\ldots$ 上应用格拉姆-施密特正交化；
找出能拟合 $f(x)$ 的最好直线。
1.希尔伯特空间：在学习了 $R^n$ 后，很自然会想到 $R^{\infty}$ 空间，它包含的向量 $v=(v_1,v_2,v_3,\ldots)$ 有无限个元素，这个空间实在太大了，我们无法控制元素 $v_j$ 大小。一个更好的想法是长度的概念不变，也就是平方和，并且只包含那些长度有限的向量：

$∥ v ∥ 2 = v 21 + v 22 + v 23 + \dots (8)$ $\begin{equation} \Vert v\Vert^2=v_1^2+v_2^2+v_3^2+\cdots\tag8 \end{equation}$

这个无限级数必须收敛到一个有限和，这样的话 $(1,\frac{1}{2},\frac{1}{3},\ldots)$ 满足，而 $(1,1,1,\ldots)$ 不满足，长度有限的向量满足可加性( $\Vert v+w\Vert\leq\Vert v\Vert+\Vert w\Vert$ ) 和数乘，所以他们形成一个向量空间，也就是希尔伯特空间。

希尔伯特空间用很自然的方法将维数变成有限的，同时还保持了欧几里得空间的空间几何。椭圆变成无限维的椭球，而垂线和之前的定义一样，当 $v,w$ 的内积为零时他们是正交的：

$v T w = v 1 w 1 + v 2 w 2 + v 2 w 3 + \dots = 0$ $v^Tw=v_1w_1+v_2w_2+v_2w_3+\cdots=0$

这个和肯定收敛，并且对于任何两个向量他们依然满足施瓦兹不等式 $|v^Tw|\leq\Vert v\Vert\Vert w\Vert$ ，即便是在希尔伯特空间，余弦值也是不可能大于1的。

对于这个空间还有一个非常结论：这里的向量可以变成函数。

2.长度和内积：假设 $f(x)=\sin x$ ，定义域为 $0\leq x\leq 2\pi$ ，函数 $f$ 就像元素是连续的向量，为了找出这种向量的长度，通常那种元素的平方和已经不适用了，此时很自然的想法是用积分替换和：

$∥ f ∥ 2 = \int 2 π 0 (f (x)) d x = \int 2 π 0 (sin x) 2 d x = π (9)$ $\begin{equation} \Vert f\Vert^2=\int_0^{2\pi}(f(x))^dx=\int_0^{2\pi}(\sin x)^2dx=\pi\tag9 \end{equation}$

希尔伯特空间变成了函数空间，向量就是函数，而且也有度量长度的方法，这个空间包含了所有长度有限的函数——类似于方程(16)。 $F(x)=1/x$ 不属于这个空间，因为 $1/x^2$ 的积分是无限的。

用积分替换和的想法同样可以用于两个函数的内积：如果 $f(x)=\sin x,g(x)=\cos x$ ，那么他们的内积是

$(f, g) = \int 2 π 0 f (x) g (x) d x = \int 2 π 0 sin x cos x d x = 0 (10)$ $\begin{equation} (f,g)=\int_0^{2\pi}f(x)g(x)dx=\int_0^{2\pi}\sin x\cos xdx=0\tag{10} \end{equation}$

这个结论就像向量内积 $f^Tg$ 一样，它依然和长度 $(f,f)=\Vert f\Vert^2$ 有关，施瓦兹不等式依然满足： $|(f,g)|\leq\Vert f\Vert\Vert g\Vert$ 。当然， $\sin x,\cos x$ 的内积为零，所以也称他们是正交的，除以他们的长度 $\sqrt{\pi}$ 后就是标准正交的。

3.傅里叶级数：函数的傅里叶级数是将其扩展到正弦和余弦形式：

$f (x) = a 0 + a 1 cos x + b 1 sin x + a 2 cos 2 x + b 2 sin 2 x + \dots$ $f(x)=a_0+a_1\cos x+b_1\sin x+a_2\cos 2x+b_2\sin 2x+\cdots$

在计算系数的时候，例如 $b_1$ ，我们在方程两边同时乘以函数 $\sin x$ ，然后计算 $0$ 到 $2\pi$ 的积分。换句话说，就是方程两边分别和 $\sin x$ 进行内积操作：

$\int 2 π 0 f (x) sin x d x = a 0 \int 2 π 0 sin x d x + a 1 \int 2 π 0 cos x sin x d x + b 1 \int 2 π 0 (sin x) 2 d x + \dots$ $\int_0^{2\pi}f(x)\sin xdx=a_0\int_0^{2\pi}\sin xdx+a_1\int_0^{2\pi}\cos x\sin xdx+b_1\int_0^{2\pi}(\sin x)^2dx+\cdots$

对于方程的右边，除了 $\sin x$ 和自身相乘外，其余都是零，这用到了方程(18)中正弦和余弦的正交性，因此 $b_1$ 就是方程左边除以右边唯一的那个非零积分项：

$b 1 = \int 2 π 0 f ( x ) sin x d x \int 2 π 0 ( sin x ) 2 d x = ( f , sin x ) ( sin x , sin x )$ $b_1=\frac{\int_0^{2\pi}f(x)\sin xdx}{\int_0^{2\pi}(\sin x)^2dx}=\frac{(f,\sin x)}{(\sin x,\sin x)}$

而对于系数 $a_1$ ，只需要用 $\cos x$ 代替 $\sin x$ 即可，对于 $a_2$ 我们使用 $\cos 2x$ 。

这里的重点是看出它和投影的相似性，向量 $b$ 在直线 $a$ 上的分量是 $b^Ta/a^Ta$ ，从上式可以看出傅里叶级数是函数 $f(x)$ 在 $\sin x$ 上的投影，它在这个方向上的分量 $p$ 是 $b_1\sin x$ 。

系数 $b_1$ 是矛盾方程 $b_1\sin x=f(x)$ 的最小二乘解，它令 $b_1\sin x$ 尽可能的靠近 $f(x)$ 。级数中的所有项都是在正弦或余弦上的投影，另外，因为他们是正交的，所以傅里叶级数给出了 $f(x)$ 相对于一组垂直轴的坐标值。

4.函数的格拉姆—施密特正交化：除了正弦和余弦外，还有许多非常有用的函数，他们不见得是正交的。最简单的例子就是 $x$ 的幂，不幸的是不存在使得他们征垂直的区间，即便是 $1,x^2$ 也不是垂直的(他们的内积始终为正)，因此对 $f(x)$ 的最佳拟合抛物线不是在 $1,x,x^2$ 上投影之和。实际上有一个类似于 $(A^TA)^{-1}$ 的矩阵，这个联系由病态的希尔伯特矩阵给出。在区间 $0\leq x\leq 1$ 上

$A T A = ⎡ ⎣ ⎢ ⎢ (1, 1) (x, 1) (x 2, 1) (1, x) (x, x) (x 2, x) (1, x 2) (x, x 2) (x 2, x 2) ⎤ ⎦ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ \int 1 \int x \int x 2 \int x \int x 2 \int x 3 \int x 2 \int x 3 \int x 4 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ 1 1 2 1 3 1 2 1 3 1 4 1 3 1 4 1 5 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥$ $A^TA=\begin{bmatrix} (1,1)&(1,x)&(1,x^2)\\ (x,1)&(x,x)&(x,x^2)\\ (x^2,1)&(x^2,x)&(x^2,x^2) \end{bmatrix}= \begin{bmatrix} \int 1&\int x&\int x^2\\ \int x&\int x^2&\int x^3\\ \int x^2&\int x^3&\int x^4 \end{bmatrix}= \begin{bmatrix} 1&\frac{1}{2}&\frac{1}{3}\\ \frac{1}{2}&\frac{1}{3}&\frac{1}{4}\\ \frac{1}{3}&\frac{1}{4}&\frac{1}{5} \end{bmatrix}$

这个矩阵的逆非常大，原因是坐标轴 $1,x,x^2$ 离垂直关系差的很远，即便我们增加几个坐标轴就会增大不垂直的可能性，我们几乎不可能用最佳十阶多项式来求解 $A^TA\hat{x}=A^Tb$ 。

再准确一点，几乎无法用高斯消元法求解；每个输入误差至少被放大了 $10^{13}$ 倍。但是我们不想放弃用多项式进行逼近，所以正确的思路就是我们将它变成正交的(利用之前提到的格拉姆-施密特正交化)，我们寻找使得 $1,x,x^2$ 正交的组合。

为了方便，我们将区间取成对称的，像 $-1\leq x\leq 1$ 这样，原因是这样会让 $x$ 的奇数幂和偶数幂正交：

$(1, x) = \int 1 - 1 x d x = 0, (x . x 2) = \int 1 - 1 x 3 d x = 0$ $(1,x)=\int_{-1}^{1}xdx=0,\quad (x.x^2)=\int_{-1}^1x^3dx=0$

因此，我们从 $v_1=1,v_2=x$ 作为前两个垂直轴开始格拉姆-施密特过程。接下来是计算第三个轴：

$v 3 = x 2 - ( 1 , x 2 ) ( 1 , 1 ) 1 - x , x 2 x , x x = x 2 - \int 1 - 1 x 2 d x \int 2 - 1 1 d x = x 2 - 1 3$ $v_3=x^2-\frac{(1,x^2)}{(1,1)}1-\frac{x,x^2}{x,x}x=x^2-\frac{\int_{-1}^1x^2dx}{\int_{-1}^21dx}=x^2-\frac{1}{3}$

用这种方式构建的多项式称为勒让德多项式，他们在 $-1\leq x\leq 1$ 区间上是正交的。

$检查一下 (1, x 2 - 1 3) = \int 1 - 1 (x 2 - 1 3) d x = [x 3 3 - x 3] 1 - 1 = 0$ $\text{检查一下}\quad \left(1,x^2-\frac{1}{3}\right)=\int_{-1}^1\left(x^2-\frac{1}{3}\right)dx=\left[\frac{x^3}{3}-\frac{x}{3}\right]_{-1}^1=0$

5.最佳直线：假设我们在区间 $[0,1]$ 上用直线 $C+Dx$ 拟合 $y=x^5$ ，至少有三种方法可以找出这样的直线：

用最小二乘法求解
$[1 x] [C D] = x 5$ $\begin{bmatrix} 1&x \end{bmatrix} \begin{bmatrix} C\\D \end{bmatrix} =x^5$ ，那么方程 $A^TA\hat{x}=A^Tb$ 就是
$[(1, 1) (x, 1) (1, x) (x, x)] [C D] = [(1, x 5) (x, x 5)] 或者 ⎡ ⎣ ⎢ ⎢ 1 1 2 1 2 1 3 ⎤ ⎦ ⎥ ⎥ [C D] = ⎡ ⎣ ⎢ ⎢ 1 6 1 17 ⎤ ⎦ ⎥ ⎥$ $\begin{bmatrix} (1,1)&(1,x)\\ (x,1)&(x,x) \end{bmatrix} \begin{bmatrix} C\\D \end{bmatrix}= \begin{bmatrix} (1,x^5)\\(x,x^5) \end{bmatrix} \quad \text{或者}\quad \begin{bmatrix} 1&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{3} \end{bmatrix} \begin{bmatrix} C\\D \end{bmatrix}= \begin{bmatrix} \frac{1}{6}\\\frac{1}{17} \end{bmatrix}$
最小化 $E 2 = \int 10 (x 5 - C - D x) 2 d x = 1 11 - 2 6 C - 2 7 D + C 2 + C D + 1 3 D 2$ $E^2=\int_0^1(x^5-C-Dx)^2dx=\frac{1}{11}-\frac{2}{6}C-\frac{2}{7}D+C^2+CD+\frac{1}{3}D^2$ ,分别对 $C,D$ 求导除以2得： $- 1 6 + C + 1 2 D = 0, - 1 7 + 1 2 C + 1 3 D = 0$ $-\frac{1}{6}+C+\frac{1}{2}D=0,-\frac{1}{7}+\frac{1}{2}C+\frac{1}{3}D=0$ ，求出解为 $\hat{C}=\frac{1}{6}-\frac{5}{14},\hat{D}=\frac{5}{17}$ 。
应用格拉姆-施密特方法用 $x-(1,x)/(1,1)$ 替换 $x$ ，也就是 $x-\frac{1}{2}$ ，它和1是正交的。然后在加上一维投影：
$C + D x = ( x 5 , 1 ) ( 1 , 1 ) 1 + ( x 5 , x - 1 2 ) ( x - 1 2 , x - 1 2 ) (x - 1 2) = 1 6 + 5 7 (x - 1 2)$ $C+Dx=\frac{(x^5,1)}{(1,1)}1+\frac{(x^5,x-\frac{1}{2})}{(x-\frac{1}{2},x-\frac{1}{2})}(x-\frac{1}{2})=\frac{1}{6}+\frac{5}{7}\left(x-\frac{1}{2}\right)$