VINS-FUSION 优化-IMU预积分因子（二）

最新推荐文章于 2024-07-22 16:19:44 发布
最新推荐文章于 2024-07-22 16:19:44 发布
阅读量634 收藏 9
点赞数 4
分类专栏： VINS-FUSION 文章标签： VINS-Fusion IMU预积分 雅克比 残差 方差
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/u010196944/article/details/135744520
版权

VINS-FUSION 优化-IMU预积分因子（一）完成了IMU预积分及对于优化变量的全部雅克比矩阵的推导，本文结合VINS-FUSION源码，完成优化-IMU预积分因子的使用。

一、IMU预积分因子雅克比

VINS-FUSION源码中将优化变量分组如下：

(p_{b_{i}}^{w}, q_{b_{i}}^{w}), (v_{i}^{w}, b_{i}^{a}, b_{i}^{g}),(p_{b_{j}}^{w}, q_{b_{j}}^{w}), (v_{j}^{w}, b_{j}^{a}, b_{j}^{g})

1.对i时刻优化变量的雅可比

jacobians[0] = \begin{vmatrix} \frac{\partial r}{\partial p_{b_{i}}^{w}} & \frac{\partial r}{\partial q_{b_{i}}^{w}} \end{vmatrix} = \begin{vmatrix} \frac{\partial r_{p}}{\partial p_{b_{i}}^{w}} & \frac{\partial r_{p}}{\partial q_{b_{i}}^{w}}\\ \frac{\partial r_{q}}{\partial p_{b_{i}}^{w}} & \frac{\partial r_{q}}{\partial q_{b_{i}}^{w}}\\ \frac{\partial r_{v}}{\partial p_{b_{i}}^{w}} & \frac{\partial r_{v}}{\partial q_{b_{i}}^{w}}\\ \frac{\partial r_{b_{a}}}{\partial p_{b_{i}}^{w}} & \frac{\partial r_{b_{a}}}{\partial q_{b_{i}}^{w}}\\ \frac{\partial r_{b_{g}}}{\partial p_{b_{i}}^{w}} & \frac{\partial r_{b_{g}}}{\partial q_{b_{i}}^{w}}\\ \end{vmatrix}

                        =\begin{vmatrix} -q_{wb_{i}}^* & \frac{1}{2} \begin{vmatrix} q_{wb_{i}}^* (p_{wb_{j}} - p_{wb_{i}} - v_{i}^{w}\Delta t + \frac{1}{2}g^w\Delta t^2) \end{vmatrix} _{\times }\\ 0 & -\begin{vmatrix} (q_{wb_{j}}^* \bigotimes q_{wb_{i}}) \end{vmatrix}_{L}\begin{vmatrix} (q_{b_{i}b_{j}}) \end{vmatrix}_{R}\\ 0 & \begin{vmatrix} q_{wb_{i}}^*(v_{j}^{w} - v_{i}^{w} + g^w\Delta t) \end{vmatrix}_{\times }\\ 0 & 0\\ 0 & 0 \end{vmatrix}

jacobians[1] = \begin{vmatrix} \frac{\partial r}{\partial v_{i}^{w}} & \frac{\partial r}{\partial b_{i}^{a}} & \frac{\partial r}{\partial b_{i}^{g}} \end{vmatrix} = \begin{vmatrix} \frac{\partial r_{p}}{\partial v_{i}^{w}} & \frac{\partial r_{p}}{\partial b_{i}^{a}} & \frac{\partial r_{p}}{\partial b_{i}^{g}} \\ \frac{\partial r_{q}}{\partial v_{i}^{w}} & \frac{\partial r_{q}}{\partial b_{i}^{a}}& \frac{\partial r_{q}}{\partial b_{i}^{g}} \\ \frac{\partial r_{v}}{\partial v_{i}^{w}} & \frac{\partial r_{v}}{\partial b_{i}^{a}} & \frac{\partial r_{v}}{\partial b_{i}^{g}} \\ \frac{\partial r_{b_{a}}}{\partial v_{i}^{w}} & \frac{\partial r_{b_{a}}}{\partial b_{i}^{a}} &\frac{\partial r_{b_{a}}}{\partial b_{i}^{g}}\\ \frac{\partial r_{b_{g}}}{\partial v_{i}^{w}} & \frac{\partial r_{b_{g}}}{\partial b_{i}^{a}}& \frac{\partial r_{b_{g}}}{\partial b_{i}^{g}}\\ \end{vmatrix}

                        =\begin{vmatrix} -q_{wb_{i}}^*\Delta t & - J_{b_{i}^{a}}^{\alpha} & - J_{b_{i}^{g}}^{\alpha}\\ 0 & 0 & - (q_{wb_{j}}^*\bigotimes q_{wb_{i}} \bigotimes q_{b_{i}b_{j}})_{L} J_{b_{i}^{g}}^{\alpha}\\ -q_{wb_{i}}^* & -J_{b_{i}^{a}}^{\beta} & -J_{b_{i}^{g}}^{\beta}\\ 0 & -I & 0\\ 0 & 0& -I \end{vmatrix}

2.对j时刻优化变量的雅可比

jacobians[2] = \begin{vmatrix} \frac{\partial r}{\partial p_{b_{j}}^{w}} & \frac{\partial r}{\partial q_{b_{j}}^{w}} \end{vmatrix} = \begin{vmatrix} \frac{\partial r_{p}}{\partial p_{b_{j}}^{w}} & \frac{\partial r_{p}}{\partial q_{b_{j}}^{w}}\\ \frac{\partial r_{q}}{\partial p_{b_{j}}^{w}} & \frac{\partial r_{q}}{\partial q_{b_{j}}^{w}}\\ \frac{\partial r_{v}}{\partial p_{b_{j}}^{w}} & \frac{\partial r_{v}}{\partial q_{b_{j}}^{w}}\\ \frac{\partial r_{b_{a}}}{\partial p_{b_{j}}^{w}} & \frac{\partial r_{b_{a}}}{\partial q_{b_{j}}^{w}}\\ \frac{\partial r_{b_{g}}}{\partial p_{b_{j}}^{w}} & \frac{\partial r_{b_{g}}}{\partial q_{b_{j}}^{w}}\\ \end{vmatrix}

                        = \begin{vmatrix} q_{wb_{i}}^* & 0\\ 0& \begin{vmatrix} (q_{b_{i}b_{j}}^{*} \bigotimes q_{wb_{i}}^* \bigotimes q_{wb_{j}}) \end{vmatrix}_{L}\\ 0 & 0\\ 0 & 0\\ 0 & 0 \end{vmatrix}

jacobians[3] = \begin{vmatrix} \frac{\partial r}{\partial v_{j}^{w}} & \frac{\partial r}{\partial b_{j}^{a}} & \frac{\partial r}{\partial b_{j}^{g}} \end{vmatrix} = \begin{vmatrix} \frac{\partial r_{p}}{\partial v_{j}^{w}} & \frac{\partial r_{p}}{\partial b_{j}^{a}} & \frac{\partial r_{p}}{\partial b_{j}^{g}} \\ \frac{\partial r_{q}}{\partial v_{j}^{w}} & \frac{\partial r_{q}}{\partial b_{j}^{a}}& \frac{\partial r_{q}}{\partial b_{j}^{g}} \\ \frac{\partial r_{v}}{\partial v_{j}^{w}} & \frac{\partial r_{v}}{\partial b_{j}^{a}} & \frac{\partial r_{v}}{\partial b_{j}^{g}} \\ \frac{\partial r_{b_{a}}}{\partial v_{j}^{w}} & \frac{\partial r_{b_{a}}}{\partial b_{j}^{a}} &\frac{\partial r_{b_{a}}}{\partial b_{j}^{g}}\\ \frac{\partial r_{b_{g}}}{\partial v_{j}^{w}} & \frac{\partial r_{b_{g}}}{\partial b_{j}^{a}}& \frac{\partial r_{b_{g}}}{\partial b_{j}^{g}}\\ \end{vmatrix}

                ​​​​​​​        =\begin{vmatrix} 0 & 0& 0\\ 0 & 0& 0\\ q_{wb_{i}}^* & 0& 0\\ 0 & I& 0\\ 0 & 0& I \end{vmatrix}

二、IMU预积分因子源码

class IMUFactor : public ceres::SizedCostFunction<15, 7, 9, 7, 9> {
   public:
    IMUFactor() = delete;
    IMUFactor(IntegrationBase* _pre_integration):pre_integration(_pre_integration) {}

    virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const {

        Eigen::Vector3d Pi(parameters[0][0], parameters[0][1], parameters[0][2]);
        Eigen::Quaterniond Qi(parameters[0][6], parameters[0][3], parameters[0][4], parameters[0][5]);

        Eigen::Vector3d Vi(parameters[1][0], parameters[1][1], parameters[1][2]);
        Eigen::Vector3d Bai(parameters[1][3], parameters[1][4], parameters[1][5]);
        Eigen::Vector3d Bgi(parameters[1][6], parameters[1][7], parameters[1][8]);

        Eigen::Vector3d Pj(parameters[2][0], parameters[2][1], parameters[2][2]);
        Eigen::Quaterniond Qj(parameters[2][6], parameters[2][3], parameters[2][4], parameters[2][5]);

        Eigen::Vector3d Vj(parameters[3][0], parameters[3][1], parameters[3][2]);
        Eigen::Vector3d Baj(parameters[3][3], parameters[3][4], parameters[3][5]);
        Eigen::Vector3d Bgj(parameters[3][6], parameters[3][7], parameters[3][8]);

        Eigen::Map<Eigen::Matrix<double, 15, 1>> residual(residuals);
        residual = pre_integration->evaluate(Pi, Qi, Vi, Bai, Bgi,
                                            Pj, Qj, Vj, Baj, Bgj);

        Eigen::Matrix<double, 15, 15> sqrt_info = Eigen::LLT<Eigen::Matrix<double, 15, 15>>(pre_integration->covariance.inverse()).matrixL().transpose();
        //sqrt_info.setIdentity();
        residual = sqrt_info * residual;

        if (jacobians) {
            double sum_dt = pre_integration->sum_dt;
            Eigen::Matrix3d dp_dba = pre_integration->jacobian.template block<3, 3>(O_P, O_BA);
            Eigen::Matrix3d dp_dbg = pre_integration->jacobian.template block<3, 3>(O_P, O_BG);

            Eigen::Matrix3d dq_dbg = pre_integration->jacobian.template block<3, 3>(O_R, O_BG);

            Eigen::Matrix3d dv_dba = pre_integration->jacobian.template block<3, 3>(O_V, O_BA);
            Eigen::Matrix3d dv_dbg = pre_integration->jacobian.template block<3, 3>(O_V, O_BG);

            if (pre_integration->jacobian.maxCoeff() > 1e8 || pre_integration->jacobian.minCoeff() < -1e8)
            {
                LOG(WARNING) << ("numerical unstable in preintegration");

                //std::cout << pre_integration->jacobian << std::endl;
                // ROS_BREAK();
            }

            if (jacobians[0])
            {
                Eigen::Map<Eigen::Matrix<double, 15, 7, Eigen::RowMajor>> jacobian_pose_i(jacobians[0]);
                jacobian_pose_i.setZero();

                jacobian_pose_i.block<3, 3>(O_P, O_P) = -Qi.inverse().toRotationMatrix();
                jacobian_pose_i.block<3, 3>(O_P, O_R) = Utility::skewSymmetric(Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt));

#if 0
            jacobian_pose_i.block<3, 3>(O_R, O_R) = -(Qj.inverse() * Qi).toRotationMatrix();
#else
                Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
                jacobian_pose_i.block<3, 3>(O_R, O_R) = -(Utility::Qleft(Qj.inverse() * Qi) * Utility::Qright(corrected_delta_q)).bottomRightCorner<3, 3>();
#endif

                jacobian_pose_i.block<3, 3>(O_V, O_R) = Utility::skewSymmetric(Qi.inverse() * (G * sum_dt + Vj - Vi));

                jacobian_pose_i = sqrt_info * jacobian_pose_i;

                if (jacobian_pose_i.maxCoeff() > 1e8 || jacobian_pose_i.minCoeff() < -1e8)
                {
                    LOG(WARNING) << ("numerical unstable in preintegration");
                    //std::cout << sqrt_info << std::endl;
                    //ROS_BREAK();
                }
            }
            if (jacobians[1])
            {
                Eigen::Map<Eigen::Matrix<double, 15, 9, Eigen::RowMajor>> jacobian_speedbias_i(jacobians[1]);
                jacobian_speedbias_i.setZero();
                jacobian_speedbias_i.block<3, 3>(O_P, O_V - O_V) = -Qi.inverse().toRotationMatrix() * sum_dt;
                jacobian_speedbias_i.block<3, 3>(O_P, O_BA - O_V) = -dp_dba;
                jacobian_speedbias_i.block<3, 3>(O_P, O_BG - O_V) = -dp_dbg;

                #if 0
                jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -dq_dbg;
                #else
                //Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
                //jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -Utility::Qleft(Qj.inverse() * Qi * corrected_delta_q).bottomRightCorner<3, 3>() * dq_dbg;
                jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -Utility::Qleft(Qj.inverse() * Qi * pre_integration->delta_q).bottomRightCorner<3, 3>() * dq_dbg;
                #endif

                jacobian_speedbias_i.block<3, 3>(O_V, O_V - O_V) = -Qi.inverse().toRotationMatrix();
                jacobian_speedbias_i.block<3, 3>(O_V, O_BA - O_V) = -dv_dba;
                jacobian_speedbias_i.block<3, 3>(O_V, O_BG - O_V) = -dv_dbg;

                jacobian_speedbias_i.block<3, 3>(O_BA, O_BA - O_V) = -Eigen::Matrix3d::Identity();

                jacobian_speedbias_i.block<3, 3>(O_BG, O_BG - O_V) = -Eigen::Matrix3d::Identity();

                jacobian_speedbias_i = sqrt_info * jacobian_speedbias_i;

                //ROS_ASSERT(fabs(jacobian_speedbias_i.maxCoeff()) < 1e8);
                //ROS_ASSERT(fabs(jacobian_speedbias_i.minCoeff()) < 1e8);
            }
            if (jacobians[2])
            {
                Eigen::Map<Eigen::Matrix<double, 15, 7, Eigen::RowMajor>> jacobian_pose_j(jacobians[2]);
                jacobian_pose_j.setZero();

                jacobian_pose_j.block<3, 3>(O_P, O_P) = Qi.inverse().toRotationMatrix();

#if 0
                jacobian_pose_j.block<3, 3>(O_R, O_R) = Eigen::Matrix3d::Identity();
#else
                Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
                jacobian_pose_j.block<3, 3>(O_R, O_R) = Utility::Qleft(corrected_delta_q.inverse() * Qi.inverse() * Qj).bottomRightCorner<3, 3>();
#endif

                jacobian_pose_j = sqrt_info * jacobian_pose_j;

                //ROS_ASSERT(fabs(jacobian_pose_j.maxCoeff()) < 1e8);
                //ROS_ASSERT(fabs(jacobian_pose_j.minCoeff()) < 1e8);
            }
            if (jacobians[3])
            {
                Eigen::Map<Eigen::Matrix<double, 15, 9, Eigen::RowMajor>> jacobian_speedbias_j(jacobians[3]);
                jacobian_speedbias_j.setZero();

                jacobian_speedbias_j.block<3, 3>(O_V, O_V - O_V) = Qi.inverse().toRotationMatrix();

                jacobian_speedbias_j.block<3, 3>(O_BA, O_BA - O_V) = Eigen::Matrix3d::Identity();

                jacobian_speedbias_j.block<3, 3>(O_BG, O_BG - O_V) = Eigen::Matrix3d::Identity();

                jacobian_speedbias_j = sqrt_info * jacobian_speedbias_j;

                //ROS_ASSERT(fabs(jacobian_speedbias_j.maxCoeff()) < 1e8);
                //ROS_ASSERT(fabs(jacobian_speedbias_j.minCoeff()) < 1e8);
            }
        }

        return true;
    }

    //bool Evaluate_Direct(double const *const *parameters, Eigen::Matrix<double, 15, 1> &residuals, Eigen::Matrix<double, 15, 30> &jacobians);

    //void checkCorrection();
    //void checkTransition();
    //void checkJacobian(double **parameters);
    IntegrationBase* pre_integration;

};

源码使用ceres解析求导：

1.构建一个继承自ceres::SizedCostFunction的类

class IMUFactor : public ceres::SizedCostFunction<15, 7, 9, 7, 9>

参数分别表示为：残差维度15，优化参数(p_{b_{i}}^{w}, q_{b_{i}}^{w})维度，优化参数(v_{i}^{w}, b_{i}^{a}, b_{i}^{g})维度，优化参数(p_{b_{j}}^{w}, q_{b_{j}}^{w})维度，优化参数(v_{j}^{w}, b_{j}^{a}, b_{j}^{g})维度。

2.重载纯虚函数

virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians)

根据输入优化参数块，实现残差和雅克比矩阵的计算。

其中：

（1）Pi,Qi表示i帧位姿，对应(p_{b_{i}}^{w}, q_{b_{i}}^{w})

（2）Vi,Bai,Bgi表示i帧速度、加速度bias、加速度bias，对应(v_{i}^{w}, b_{i}^{a}, b_{i}^{g})

（3）Pj,Qj表示i帧位姿，对应(p_{b_{j}}^{w}, q_{b_{j}}^{w})

（4）Vj,Baj,Bgj表示i帧速度、加速度bias、加速度bias，对应(v_{j}^{w}, b_{j}^{a}, b_{j}^{g})

雅可比矩阵J_{b_{i}^{a}}^{\alpha },J_{b_{i}^{g}}^{\alpha },J_{b_{i}^{a}}^{\beta},J_{b_{i}^{g}}^{\beta},J_{b_{i}^{g}}^{q}是在预积分中实现。

3.残差求解evaluate
Eigen::Matrix<double, 15, 1> evaluate(
	const Eigen::Vector3d &Pi, const Eigen::Quaterniond &Qi, const Eigen::Vector3d &Vi, const Eigen::Vector3d &Bai, const Eigen::Vector3d &Bgi,
	const Eigen::Vector3d &Pj, const Eigen::Quaterniond &Qj, const Eigen::Vector3d &Vj, const Eigen::Vector3d &Baj, const Eigen::Vector3d &Bgj) {
	/// NOTE: xxx

	Eigen::Matrix<double, 15, 1> residuals;

	Eigen::Matrix3d dp_dba = jacobian.block<3, 3>(O_P, O_BA);
	Eigen::Matrix3d dp_dbg = jacobian.block<3, 3>(O_P, O_BG);

	Eigen::Matrix3d dq_dbg = jacobian.block<3, 3>(O_R, O_BG);

	Eigen::Matrix3d dv_dba = jacobian.block<3, 3>(O_V, O_BA);
	Eigen::Matrix3d dv_dbg = jacobian.block<3, 3>(O_V, O_BG);

	Eigen::Vector3d dba = Bai - linearized_ba;
	Eigen::Vector3d dbg = Bgi - linearized_bg;

	Eigen::Quaterniond corrected_delta_q = delta_q * Utility::deltaQ(dq_dbg * dbg);
	Eigen::Vector3d corrected_delta_v = delta_v + dv_dba * dba + dv_dbg * dbg;
	Eigen::Vector3d corrected_delta_p = delta_p + dp_dba * dba + dp_dbg * dbg;

	residuals.block<3, 1>(O_P, 0) = Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt) - corrected_delta_p;
	residuals.block<3, 1>(O_R, 0) = 2 * (corrected_delta_q.inverse() * (Qi.inverse() * Qj)).vec();
	residuals.block<3, 1>(O_V, 0) = Qi.inverse() * (G * sum_dt + Vj - Vi) - corrected_delta_v;
	residuals.block<3, 1>(O_BA, 0) = Baj - Bai;
	residuals.block<3, 1>(O_BG, 0) = Bgj - Bgi;
	return residuals;
}

jacobians组成如下：

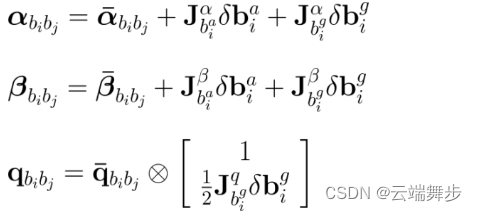注：待优化变量如上，但实际求雅可比矩阵是用的优化变量的误差量（扰动量）。

故：dp_dba表示残差p对ba的雅可比矩阵，对应jacobians第0行9列，dp_dbg、dq_dbg、dv_dba、dv_dbg如图就很好理解了。

4.雅克比矩阵

雅克比矩阵对应小节一中IMU预积分因子雅克比公式。

5.方差矩阵

代码中sqrt_info表示信息矩阵，等于方差的逆矩阵，如下：

Eigen::Matrix<double, 15, 15> sqrt_info = Eigen::LLT<Eigen::Matrix<double, 15, 15>>(pre_integration->covariance.inverse()).matrixL().transpose();

​​​​​​​

三、参考

1.VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator

2.Online Temporal Calibration for Monocular Visual-Inertial Systems

3.https://github.com/HKUST-Aerial-Robotics/VINS-Fusion

4.多传感器融合定位-基于图优化的建图方法

云端舞步
关注
  • 4
    点赞
  • 踩
  • 9
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
VINS-fusion双目+imu数据集
12-28
可以直接下载使用的VINS-FUSION数据集，启动vins定位后，在这个数据集的目录下，使用rosbag play V1_01_easy.bag播放数据集即可
VINS-Fisheye:鱼眼版的VINS-Fusion
04-06
基本软件环境与VINS-Fusion相同。 此外，它需要OpenCV cuda版本（仅在OpenCV 3.4.1上进行测试）。 Visionworks：可选 如果要使用此软件包的CUDA模式，则深度估计需要使用 。 2.用法 2.1更改CMakeLists中的opencv路径
VINS-FUSION 优化-IMU预积分因子（三）
最新发布
u010196944的博客
07-22 439
给出两种推导方差的方法：基于一阶泰勒展开的误差递推方程和基于误差随时间变化的递推方程。并详细给出VINS-Fusion IMU预积分基于误差随时间变化的递推方程。同时给出bias变化后，预积分泰勒展开形式的雅克比矩阵J的求解。 ​
VINS-FUSION 优化-IMU预积分因子（一）
u010196944的博客
07-22 325
从IMU常规中值积分引出预积分，并求得IMU预积分因子对优化变量的全部雅克比矩阵，
VINS-FUSION 前端后端代码全详解
热门推荐
lovely_yoshino的博客
07-16 1万+
本次工作 我首先一步步的把代码全部注释了，十分的详细，对于C++和OpenCV的一些操作也进行了详细的注释，对于刚入门的同学应该还是有帮助的。之后我将代码开源，并写了相应的博客进行讲解。 1. 程序入口rosNodeTest.cpp 1.1 定义内容 运行程序时，首先进入的是主程序vins_estimator/src/estimator/rosNodeTest.cpp 里边主要定义了 估计器、 缓存器 、 获取传感器数据的函数 和 一个主函数 // 获得左目的message void img0_callb
VINS-FUSION 优化-视觉误差因子
u010196944的博客
07-22 574
本文从论文公式到相对应源码，详细叙述了深度/逆深度参数，从第i帧到j帧重投影误差表示视觉误差因子。
bench_ws:用于与不同状态估计算法（即 VINS-Mono、VINS-Fusion、ORBSLAM3、Stereo-MSCKF 等）进行比较的 catkin 工作区
05-29
长凳_ws 用于对不同状态估计算法进行基准测试的 catkin 工作区，即： 建造 构建过程相当自动化，此 repo 假设您在安装了 Ubuntu 18.04 的 linux 机器上运行。 然后要使用此存储库，您将发出以下命令， ...
VINS-Fusion.zip
03-16
VINS-Fusion是一种基于视觉惯性导航系统的融合算法，它结合了来自摄像头的图像数据（视觉信息）和惯性测量单元（IMU）的数据来实现对移动设备的精确定位和姿态估计。在SLAM（Simultaneous Localization And Mapping...
VINS 中的IMU预积分推导和代码解读.zip
06-06
本文将深入探讨VINS中的IMU预积分推导及其代码实现。 首先，理解IMU预积分的概念至关重要。IMU数据包括加速度计和陀螺仪的读数，它们分别提供了线加速度和角速度信息。由于传感器的采样间隔和计算延迟，直接利用...
VINS-Fusion_footsteps
03-16
VINS-Fusion是的扩展，它支持多种视觉惯性传感器类型（单摄像机+ IMU，立体摄像机+ IMU，甚至仅立体摄像机）。 我们还展示了一个将VINS与GPS融合的玩具示例。 特征： 支持多种传感器（立体声摄像机/单镜头摄像机+ ...
VINS-fusion 论文
10-05
VINS-fusion是一种视觉与IMU融合的SLAM技术，旨在将视觉传感器和惯性传感器的数据融合，以实现高精度的状态估计。VINS-fusion技术可以应用于各种机器人应用，包括机器人探险、自动驾驶、虚拟现实和增强现实等。
VINS-Fusion
04-02
VINS-Fusion通过优化算法确保两种传感器数据的有效对齐，从而提高整体定位性能。 "VINS-Fusion-master"这个文件名表明这是VINS-Fusion项目的主分支代码库，通常包含源代码、文档、示例数据以及编译和运行项目所需的...
鱼眼版的VINS-Fusion-C/C++开发
05-27
该存储库是具有GPU和Visionworks加速功能的VINS-Fusion的Fisheye版本。 它可以在Nvidia TX2上实时运行，还可以基于鱼眼提供深度估计。 VINS-Fisheye此存储库是具有GPU和Visionworks加速功能的VINS-Fusion的Fisheye...
matlab建立汽车模型代码-VINS-Fusion:WINES-Fusion
06-08
可以在VINS-Fusion/analysis/ntuviral_vinsfusion文件夹中找到VINS-Fusion/analysis/ntuviral_vinsfusion 。 只需运行 MATLAB 脚本checkall_parallel.m ，结果就会被打印出来。 如果您在工作中使用 NTU VIRAL 数据集...
vins-application:VINS-Fusion，VINS-Fisheye应用程序在不同的板上（包括台式机和Jetson板）使用不同组的相机和imu
03-31
分支名称>-单分支 经过测试：Jetson Xavier NX，Jetson Xavier AGX，Jetson TX2，Intel i7-6700k，i7-8700k，i9-10900k，i5-9600k结果片段：带屏蔽的PX4的VINS-Fusion：指数1.2.3.先决条件●：必须输入VINS（首先...
适用于Ubuntu20.04的VINS-mono源码
05-22
适用于Ubuntu20.04的VINS-mono源码，与官方源码比，修复了在Ubuntu20.04上编译时出现CV_FONT_HERSHEY_SIMPLEX未定义、‘CV_RGB2GRAY’ was not declared等错误。
VINS-Mono代码注释.7z
09-03
VINS-Mono是一种视觉惯性导航系统（Visual-Inertial Navigation System），它是基于单目摄像头和惯性测量单元（IMU）的实时定位与建图算法。这个压缩包"VINS-Mono代码注释.7z"包含了VINS-Mono算法的源代码以及相关的...
VINS-Mono代码注释，仅供学习
01-02
4. **非线性优化**：VINS-Mono通常采用基于因子图的优化框架，如g2o或Ceres Solver，解决SLAM问题。理解因子图模型和Levenberg-Marquardt等优化算法是必要的。 5. **状态估计**：包括位姿估计、里程计（odometry）...
vins-fusion显示wait for imu
07-28
回答: 当VINS-Fusion显示"wait for imu"时，可能是由于以下原因之一导致的。首先，VINS-Fusion的主线程(main())订阅IMU数据，如果没有接收到IMU数据，它会一直等待。这可能是因为IMU设备未连接或未正常工作。其次，VINS-Fusion的测量线程(processmeasurements())也会使用IMU数据进行预积分和VIO初始化等操作，如果IMU数据不可用，它也会等待。最后，确保在使用VINS-Fusion时，相机和IMU设备都已正确连接并配置。\[2\]\[3\] #### 引用[.reference_title] - *1* *3* [Intel RealSense D435i与IMU标定用于vins-fusion](https://blog.csdn.net/z1872385/article/details/126621326)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v91^control_2,239^v3^insert_chatgpt"}} ] [.reference_item] - *2* [（1）VINS-Fusion的代码前端 （笔记）](https://blog.csdn.net/qq_42221707/article/details/126314811)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v91^control_2,239^v3^insert_chatgpt"}} ] [.reference_item] [ .reference_list ]

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值