简介:
本文主要介绍几种基于灰度的图像匹配算法:平均绝对差算法(MAD)、绝对误差和算法(SAD)、误差平方和算法(SSD)、平均误差平方和算法(MSD)、归一化积相关算法(NCC)、序贯相似性检测算法(SSDA)、hadamard变换算法(SATD)。下面依次对其进行讲解。
MAD算法
介绍
平均绝对差算法(Mean Absolute Differences,简称MAD算法),它是Leese在1971年提出的一种匹配算法。是模式识别中常用方法,该算法的思想简单,具有较高的匹配精度,广泛用于图像匹配。
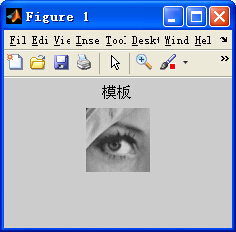
设S(x,y)是大小为mxn的搜索图像,T(x,y)是MxN的模板图像,分别如下图(a)、(b)所示,我们的目的是:在(a)中找到与(b)匹配的区域(黄框所示)。
算法思路
在搜索图S中,以(i,j)为左上角,取MxN大小的子图,计算其与模板的相似度;遍历整个搜索图,在所有能够取到的子图中,找到与模板图最相似的子图作为最终匹配结果。
MAD算法的相似性测度公式如下。显然,平均绝对差D(i,j)越小,表明越相似,故只需找到最小的D(i,j)即可确定能匹配的子图位置:
其中:
算法评价:
优点:
①思路简单,容易理解(子图与模板图对应位置上,灰度值之差的绝对值总和,再求平均,实质:是计算的是子图与模板图的L1距离的平均值)。
②运算过程简单,匹配精度高。
缺点:
①运算量偏大。
②对噪声非常敏感。
——————————————————————————————————————————————————————————————————————————————
SAD算法
介绍
绝对误差和算法(Sum of Absolute Differences,简称SAD算法)。实际上,SAD算法与MAD算法思想几乎是完全一致,只是其相似度测量公式有一点改动(计算的是子图与模板图的L1距离),这里不再赘述。
算法实现
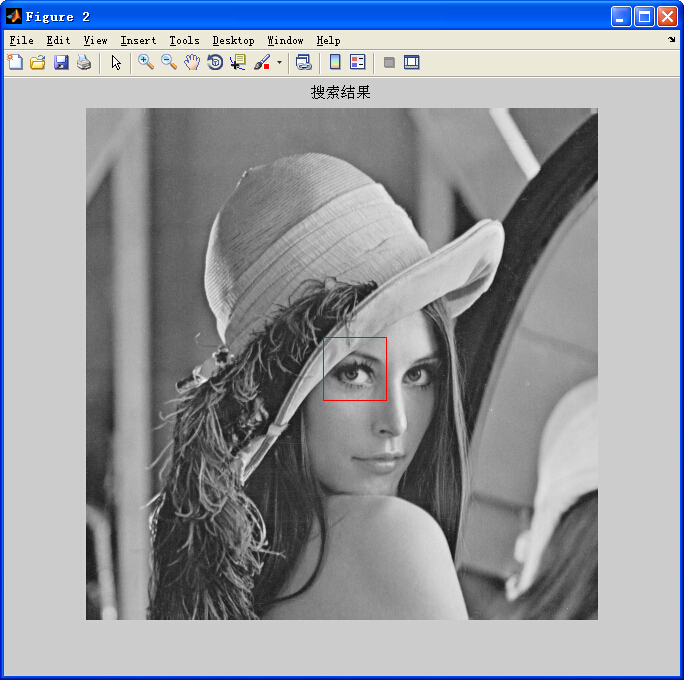
由于文章所介绍的几个算法非常相似,所以本文仅列出SAD算法的代码,其余算法的实现类似。看别人代码都相对费力,想自己敲也很简单。
MATLAB代码
输出结果
——————————————————————————————————————————————————————————————————————————————
SSD算法
误差平方和算法(Sum of Squared Differences,简称SSD算法),也叫差方和算法。实际上,SSD算法与SAD算法如出一辙,只是其相似度测量公式有一点改动(计算的是子图与模板图的L2距离)。这里不再赘述。
——————————————————————————————————————————————————————————————————————————————
MSD算法
平均误差平方和算法(Mean Square Differences,简称MSD算法),也称均方差算法。实际上,MSD之余SSD,等同于MAD之余SAD(计算的是子图与模板图的L2距离的平均值),故此处不再赘述。
————————————————————————————————————————————————————————————————————————————————
NCC算法
归一化积相关算法(Normalized Cross Correlation,简称NCC算法),与上面算法相似,依然是利用子图与模板图的灰度,通过归一化的相关性度量公式来计算二者之间的匹配程度。
其中,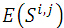

————————————————————————————————————————————————————————————————————————
SSDA算法
序贯相似性检测算法(Sequential Similiarity Detection Algorithm,简称SSDA算法),它是由Barnea和Sliverman于1972年,在文章《A class of algorithms for fast digital image registration》中提出的一种匹配算法,是对传统模板匹配算法的改进,比MAD算法快几十到几百倍。
与上述算法假设相同:S(x,y)是mxn的搜索图,T(x,y)是MxN的模板图,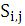
显然: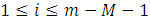
SSDA算法描述如下:
①定义绝对误差:
其中,带有上划线的分别表示子图、模板的均值:
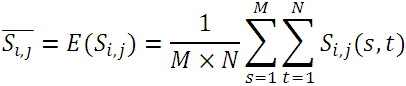
实际上,绝对误差就是子图与模板图各自去掉其均值后,对应位置之差的绝对值。
②设定阈值Th;
③在模板图中随机选取不重复的像素点,计算与当前子图的绝对误差,将误差累加,当误差累加值超过了Th时,记下累加次数H,所有子图的累加次数H用一个表R(i,j)来表示。SSDA检测定义为:
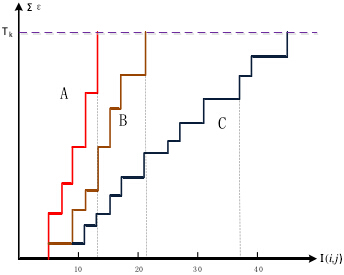
下图给出了A、B、C三点的误差累计增长曲线,其中A、B两点偏离模板,误差增长得快;C点增长缓慢,说明很可能是匹配点(图中Tk相当于上述的Th,即阈值;I(i,j)相当于上述R(i,j),即累加次数)。
④在计算过程中,随机点的累加误差和超过了阈值(记录累加次数H)后,则放弃当前子图转而对下一个子图进行计算。遍历完所有子图后,选取最大R值所对应的(i,j)子图作为匹配图像【若R存在多个最大值(一般不存在),则取累加误差最小的作为匹配图像】。
由于随机点累加值超过阈值Th后便结束当前子图的计算,所以不需要计算子图所有像素,大大提高了算法速度;为进一步提高速度,可以先进行粗配准,即:隔行、隔离的选取子图,用上述算法进行粗糙的定位,然后再对定位到的子图,用同样的方法求其8个邻域子图的最大R值作为最终配准图像。这样可以有效的减少子图个数,减少计算量,提高计算速度。
——————————————————————————————————————————————————————————————————————
SATD算法
hadamard变换算法(Sum of Absolute Transformed Difference,简称SATD算法),它是经hadamard变换再对绝对值求和算法。hadamard变换等价于把原图像Q矩阵左右分别乘以一个hadamard变换矩阵H。其中,hardamard变换矩阵H的元素都是1或-1,是一个正交矩阵,可以由MATLAB中的hadamard(n)函数生成,n代表n阶方阵。
SATD算法就是将模板与子图做差后得到的矩阵Q,再对矩阵Q求其hadamard变换(左右同时乘以H,即HQH),对变换都得矩阵求其元素的绝对值之和即SATD值,作为相似度的判别依据。对所有子图都进行如上的变换后,找到SATD值最小的子图,便是最佳匹配。
MATLAB实现:
输出结果:
—————————————————————————————————————————————————————————————————————









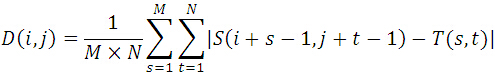
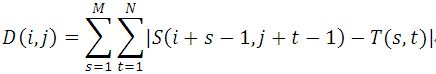
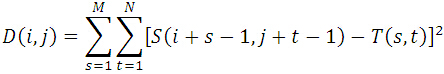
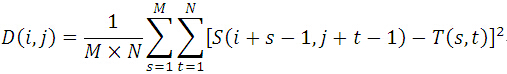
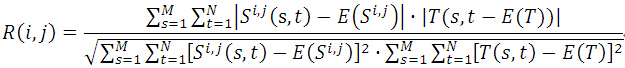

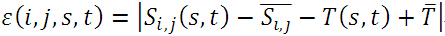

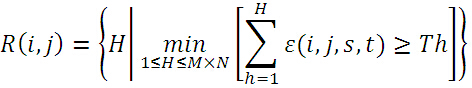















 4771
4771

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








