数学微积分

之前写了概率论的学习笔记，今天决定写点微积分的内容。以前中学时一直觉得微积分这个名字很高大上，尤其对微分有种不明觉厉的感觉，后来上了大学真学了微积分才发现，其实微分和积分不是平级的概念，真正和积分平起平坐的是中学就学过的导数，积分和导数互为逆运算，它俩才是平级的。而微分真正的地位是什么呢？书中导数章节快要结束时才提了下微分的计算，说已知导数就能算出微分，当时看了感觉很画蛇添足又无足轻重，让人觉得微分的地位简直对不起微积分这个名字。我也曾对它们的本质感兴趣，不过最终也仅限于考试没有深究。

毕业后读了不少别人的文章与书籍，才知道原来微积分最早是从微分来的，因为不够严谨在创立200年后被用极限定义的微积分取代，这才有了我们现在学的微积分，曾经迷惑的我渐渐明白了前因后果也对微积分有了更多兴趣，于是从源流和历史的角度重新学习了下微积分的由来，于是也自己写了些笔记，篇幅有限就把基本内容写成了这篇文章。

1、积分的由来

积分的思想最初来自于割圆法，即用近似方法求出圆的面积。圆可以划分出若干个全等三角形，而三角形的面积公式是已知的，所以求出每个三角形的面积，加在一起，就可近似得出圆的面积。设划分数量为 ，三角形高为 ，底边长 ，则近似面积 。

 

 

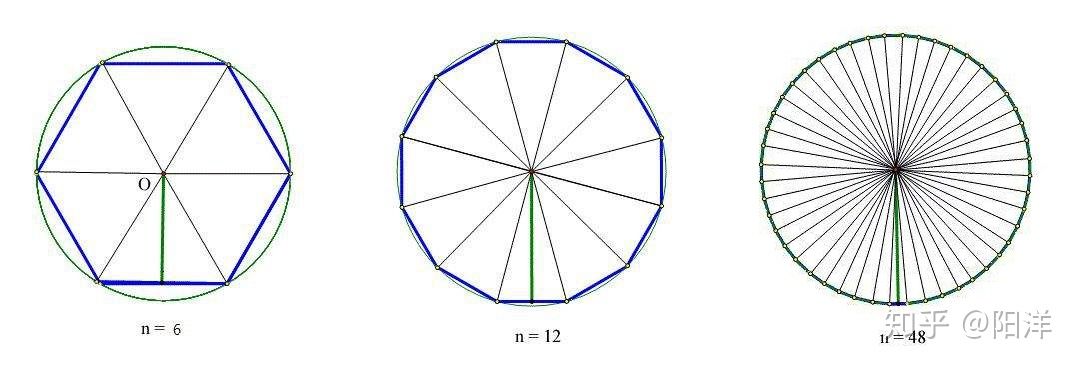
如图所示，当三角形数量较少时所得面积与圆面积差距较大，但随着划分的三角形数量增加，近似程度逐渐升高，得出的面积越来越近似于圆真正的面积。三角形的高也越来越接近圆的半径，底片也趋于和对应弧长重合。

所以分割数量足够多，多到三角形的高与圆的半径长度差距可以忽略不计，三角形底边与三角形弧长的差距也可忽略不计，那么高 等于圆半径 ，底边长根据圆周长公式为 ，所以面积 ，而结果 正是圆面积公式。

 

 

2、求积分

这种思想在圆面积上的应用是成功的，而当解析几何出现后，我们同样也可以把这种方法应用在坐标系中的函数曲线上，例如求抛物线函数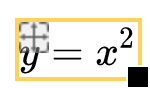 从坐标轴0点到 点处的面积，跟圆形近似成三角形累加一样，现在我们把这个面积近似成长方形累加起来。

 

还是同样的方法除以一个足够大的数n，那么每个长方形的底边就被均分成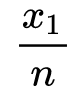 ，而长方形的高则是对应位置的 代入函数得到的 值，由于是均分所以每次 值累加一倍，代入函数后 依次为 ，所以面积所以小四边形累加的和为： 提取公因式并化简后为 继续进行数列求和为 由于n足够大所以分母带n的数可视为0，最后我们得到答案面积为 ，如果不代入坐标 那就是 ，也正是抛物线函数 求积分所得原函数，这就是积分的由来！对一个曲线函数求在具体距离上围成的就是定积分，而如果你不把数带进去，得到的就是个关于面积的函数，它也是已知导函数求它的原函数。（当然这里还有点不严谨，应该带个常数C）

 

 

最后说一下积分书写格式，因为用这种思想解决问题都需要除以一个相当于无穷大的数 来获得一个相当于无穷小的底边，但圆的无穷小底边和抛物线问题的无穷小底边表达式不一样，所以统一用符号 表示，而 则拉成变成了积分的专有符号 ，刚才问题中抛物线 围成面积在x轴上是从0到 ，所以标准写法就是 ，不代入任何数字则是不定积分 （前面提到的常数C，因为 加任何常数求导都还是 ）

 

3、古典微积分中的导数

说完了积分，接着说说和它互为逆运算的导数（即求导），积分来自几何中的面积问题，而导数也源于几何，来自于切线斜率这一问题。

直接求经过曲线上一点的直线(切线)的斜率无从下手，但如果求过两个点的直线(割线)斜率，则可用三角函数解决。以割线与曲线的两个交点作直角三角形，三角形的对边除以邻边，可得三角函数中的正切值，正是这条直线的斜率。

如图所示，两交点连线所成直角三角形中，用蓝色标出的角的正切值即为斜率。正切=对边/邻边,分别设邻边、对边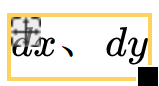为 ，则正切为 。两条边长等于坐标的差值，例如交点坐标是点 点 ，则邻边是 对边是 ，斜率值即 ,由于y是由x代入函数所得，所以也能写成 。

 

 

 

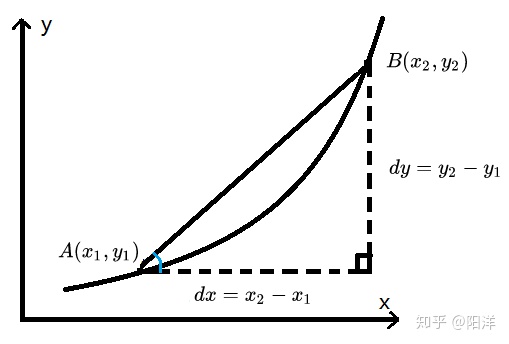
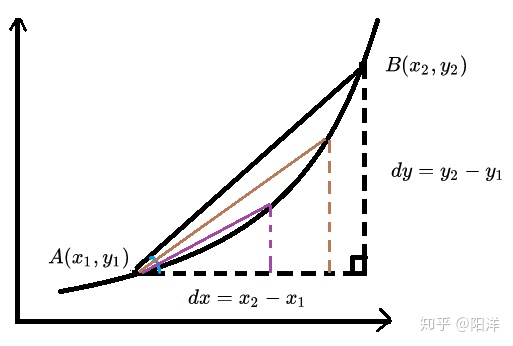
割线的斜率已经知道了，但我们想要的是切线斜率，这时候我们发现，如果让直线与曲线的两个交点离得近一些，这条割线也就更近似于切线，斜率也更接近切线的斜率。如图所示割线的另一个交点与想求切线的点 越近，则跟过该点 的切线的近似程度越高。

 

例如求与函数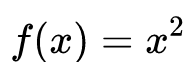 在 点上切线斜率相近似的割线斜率， 外另一个交点为 的割线，肯定比另一个交点为 的割线近似程度更高。

 

既然割线的两个点越近，近似于切线的程度也越高，就越接近我们的目标。那干脆让割线的两个交点重合，直接变成切点，可以吗？想法很好，但从图中可以看出，随两个点越来越近，这个过程中三角形越来越小，边长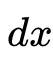 和 自然也越来越小，如果另一个交点真的和切点重合，那就没有边长，没有边长也就更没有正切了。

 

所以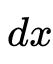 与 不能没有，但又要小到可以忽略，于是现在就称 与 为无穷小，这就是微分！无穷小即是古典微积分中微分的定义。（回顾类比之前讲过的积分，积分中dx也是无穷小，不过是另一种无穷小----底边的无穷小）

 

现在回到求曲线函数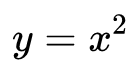 或者叫 在点 上的切线斜率问题上来，邻边 现在是无穷小，而对边 是 与 的差值，y值要靠代入x计算得出，于是就把含有无穷小的x值代入原函数，得 ，展开后得 ，减去抵消的项最后得到带着微分dx的对边变成长 。

 

现在再用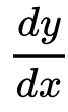 ，代入后得那么 ，将微分dx上下约去后得 ,dx是无穷小可以忽略，所以把dx省去最终得到 ，把推导过程从头到尾连续写出来则如下图所示：

 

如果把曲线上点 的坐标代入，那么得到的就是过该点切线的斜率，如果不代入，那么得到的就是 这个关于该曲线所有点切线斜率的函数，这就是导数！

 

以上写成标准形式即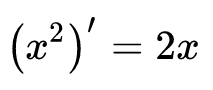

 

综上所述，古典微积分用斜率定义了导数，又利用无穷小也就是微分求出了斜率。这个过程很直观但存在一个严重的问题，就是无穷小一会被当成0省去一会又被当成非0数用除法约去，虽然我们能用这个方法获得导数，但无法解释的无穷小对数学的严格性造成了挑战，这个问题在微积分诞生后200年才获得了解决，那就是建立在极限基础上的现代微积分。

 

4、用极限定义的现代微积分

极限的定义是一种变化趋势。可以用符号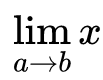 表示，字母lim表示求极限，lim右侧是求极限的对象(可以是函数等)，lim下方的存在变化趋势的具体内容，变化内容一般是函数x轴取值，也可以是其他量。

 

用极限定义现代微积分写成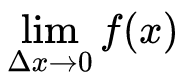 这一形式。这个极限的变化量是邻边边长也就是原来的 ，之前邻边长 代表的是无穷小也就是微分，但现在仅仅是一个变化量用 表示。剩下的步骤和之前一样，只是最后一步时 取极限趋近于0全部消去。所以实际上现代微积分是用极限这个概念规避了无穷小的麻烦，之前所有步骤邻边长都是一个非0的数自然可以约去，只是最后一步求极限趋于0消去了。

 

这样在推导过程用不到无穷小，一会是0一会非0的麻烦也就避开了，不过我们虽然没有了无穷小的麻烦，微分这个原本是微积分起点的概念也连带没有了。现在微分已经没必要求了，但想再表示微分也不是不行，以前是先有微分再求导数，现在直接有了导数也可以再求微分，已知导数后再乘以变化量就可以求出微分，不过这个微分的定义就成了变化的具体数值，跟原来不一样了，这也就是书中导数章节末尾最后那一点微分内容的由来，算是历史的孑遗吧。

其实极限作为单独一门学科，内容与应用还有许多，不过这里仅说了重新定义求导方式这一件事，有兴趣可以再多看看其他的。

用极限求函数的导数过程示意

5、对本质的理解

最后回到回到微积分的核心“导数”和“积分”上来，它们的本质究竟是什么，你可能会想前面不都已经说了导数是斜率，但斜率只是导数的几何意义。几何意义并不是本质，只是一种实际意义，意义可以是几何意义，也可以是物理意义。莱布尼茨发现微积分是用的斜率，而在牛顿那里则是通过瞬时变化率，这两者都是导数的意义。

我认为更基本的说是它们都是运算，只不过是一种特殊的运算，导数是一种特殊的求商，积分是一种特殊的求积，特殊在乘除的数不是普通的数，而是无穷小。积分的 符号和阶乘的 号、取对数的 符号一样都是运算，但即使有复杂或特殊性它们也都是在基本乘除运算的基础上建立的，微积分的特殊在包含了无穷小，当然这是从古典微积分的角度说的，如果从现代的角度，那么导数和积分无疑都是极限，而极限某种程度上也可看作一种运算。

 

运算本身是没有意义的，但联系现实赋予了它们意义。就像阶乘的 说白了只是一个递归形式的乘法运算，但在排列组合中的应用赋予了它现实意义。微积分解决了很多诸如斜率、面积等没法直接解决的问题，同时带来了很多好用的性质可以研究最值、单调性等等，从17世纪的弹道学到各种领域广泛改变了人们的生活，我想就都它对我们的意义吧。