坐标变换中，矩阵左乘和右乘的区别

star-keke

已于 2023-07-19 15:32:07 修改

阅读量3.5k

点赞数 1

文章标签：矩阵算法

于 2023-07-18 17:35:03 首次发布

本文链接：https://blog.csdn.net/u011208918/article/details/131791369

版权

一、矩阵相乘的性质

乘法结合律： (AB)C=A(BC)．
乘法左分配律：(A+B)C=AC+BC
乘法右分配律：C(A+B)=CA+CB
对数乘的结合性k(AB）=(kA)B=A(kB）．
转置 (AB)T=BTAT．

矩阵乘法一般不满足交换律。矩阵放到左边和右边是要进行装置。

二、理论推导

对于两个变换的叠加： $M_{2}M_{1}$ 表示先进行 $M_{1}$ 变换，再进行 $M_{2}$ 变换，这里 $M_{1}$ 、 $M_{2}$ 都是自然基坐标系下。
如果 $M_{2}$ 变换是在 $M_{1}$ 坐标系基础上进行的，那么根据相似矩阵把 $M_{2}$ 转换成自然基坐标系下： $M_{1}M_{2}M_{1}^{-1}$
那么两个变换叠加就是： $(M_{1}M_{2}M_{1}^{-1})M_{1} = M_{1}M_{2}$

这是一个很有意思的现象，如果每个变换都是在上个变换基础上进行的，那么只要把矩阵顺序反过来即可：

所有变换都在自然基下： $M_{4}M_{3}M_{2}M_{1}$
每个变换在前一个变换后的坐标系下： $M_{1}M_{2}M_{3}M_{4}$

三、结论

左乘是以固定（世界）坐标为参考的变换。右乘当前（本地）坐标系是以系为参考的变换。

四、验证实例

如向量P（红色矩形），移动矩阵 $M_{1}$ （向x方向移动200个像素），旋转矩阵 $M_{2}$ （顺时针旋转90度），P的初始位置位于世界坐标中心O处，局部坐标系o'和世界坐标系o重合。

向量右乘： $M_{1}M_{2}$

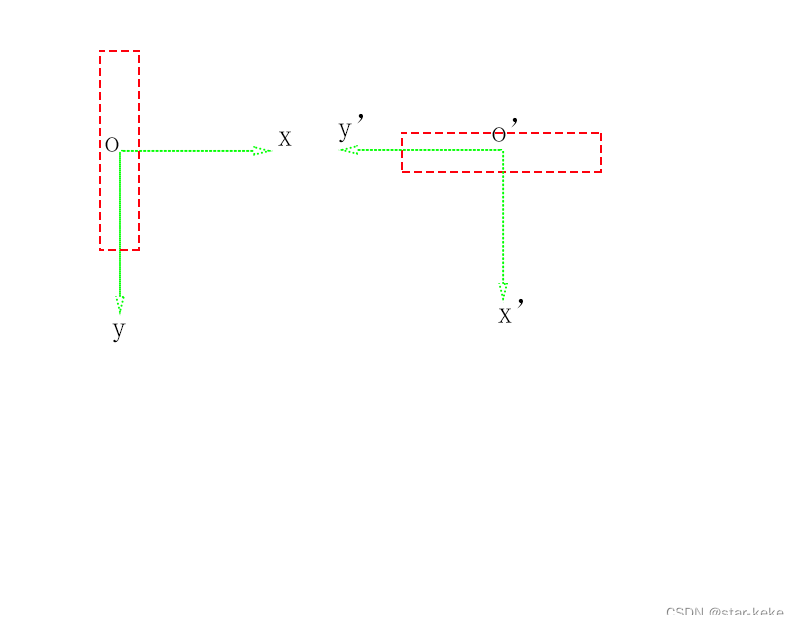
可以看出，红框移动到o'处，并以o'为中心旋转了90度，o'为局部坐标系

向量左乘： $M_{2}M_{1}$

可以看出，红框移动到右边，并以o为中心旋转了90度，此时o‘在下方’

可以看出，左乘和右乘的结果不一样

以上结论以通过测试，附上qt的测试代码：

Widget::~Widget()
{
    delete ui;
}



void Widget::paintEvent(QPaintEvent *event)
{
    QPainter painter(this);
    painter.setWindow(-400,-300,800,600);

    QPointF p1(-20,-100), p2 (20,100);
    painter.drawRect(QRectF(p1, p2));

    Eigen::Matrix3d M1;
    M1 << 1,0,200,
         0,1,0,
         0,0,1;

    Eigen::Matrix3d M2;
    double r = 90*3.1415926/180;
    M2 << cos(r), -sin(r), 0,
            sin(r), cos(r), 0,
            0,0,1;

    Eigen::Vector3d p3 {p1.x(), p1.y(),1};
    Eigen::Vector3d p4 {p2.x(), p2.y(),1};

#if 1
    //右乘
    Eigen::Vector3d p5 = M1*M2*p3;
    Eigen::Vector3d p6 = M1*M2*p4;
#else
    //左乘
    Eigen::Vector3d p5 = M2*M1*p3;
    Eigen::Vector3d p6 = M2*M1*p4;

#endif

    QPointF p7(p5.x(), p5.y()), p8 (p6.x(), p6.y());
    painter.setPen(Qt::red);
    painter.drawRect(QRectF(p7, p8).normalized());
}