脑图的空间零模型比较

摘要

技术和数据共享使得高分辨率大脑结构和功能图的数量大幅增加。现代神经成像研究越来越依赖于识别这些地图拓扑之间的对应关系；然而，大多数标准的统计推断方法没有考虑到它们的空间特性。目前，有多种方法被开发用于生成零分布，以保留脑图的空间自相关性，并产生更准确的统计估计。本文全面评估了十种已发表的零框架在神经成像数据统计分析中的性能。为了测试这些框架的有效性，首先将它们应用于一系列模拟情境中，并检查数据分辨率和空间自相关性对其整体错误率(FWER)的影响。其次，每个框架都有两个神经成像数据集，研究它们在测试脑图(例如，将两个激活图关联起来)和分区内特征空间分布(例如，量化内在功能网络中激活图的特异性)之间对应关系时的性能。最后，本研究考察了这些零模型的实现差异如何影响它们的性能。与先前的报告一致，本研究发现不保留空间自相关性的朴素零模型始终会产生较高的假阳性率和不切实际的宽松统计估计值。虽然空间受限的零模型提供了更真实、更保守的估计，但是这些框架仍然存在虚高的假阳性率和分析性能差异。在整个结果中，本研究观察到分区和分辨率对零模型性能的影响最小。总之，本研究结果强调了继续开发统计学上严谨的脑图比较方法的必要性，并为未来的研究比较和基准测试提供了一个统一的框架。

引言

大脑由一系列嵌套的、功能多样化的神经回路组成。这些回路之间的连接和相互作用最终表现为结构和功能特性的独特地形分布。成像、追踪和记录技术的最新进展，以及全球数据共享计划，已经产生了许多高分辨率地图，包括基因表达、细胞学、受体密度、皮质内髓鞘以及功能组织。

越来越多的现代神经成像研究涉及到识别脑地图之间的对应关系，然而传统的统计推断方法在进行这种比较时并不适用。也就是说，在空间嵌入式系统中(如大脑)，相邻的数据点并不是统计独立的，这违反了许多常见推断框架的假设。以计算两个脑图之间的相关性为例，当使用标准参数零模型(例如，t分布)时，地图的空间自相关性违反了模型误差独立同分布(i.i.d.)的要求。当使用标准非参数零模型(例如，对其中一个特征地图进行随机排列)时，空间自相关性违反了可置换性的要求。在这两种情况下，计算出的p值会被夸大，从而导致不同分析的整体误差率(FWER或I型错误率)增加。

神经影像中的空间零模型可分为两大类：非参数空间置换模型和参数化数据模型。在非参数空间置换模型中，大脑皮层表面被表示为一个球体，对其进行随机旋转，生成具有随机拓扑但有相同空间自相关性的表面地图。在参数化数据模型中，通过估计经验脑地图的空间自相关性，并利用其生成具有随机拓扑和类似(但不完全相同)空间自相关性的替代零模型。自开发以来，这些模型已被一些研究人员采用。据所知，至少有十种不同的零模型框架可用于脑图的统计估计。

这些零模型的最早实现之一(由Alexander-Bloch等人(2013)提出)，描述了一种使皮层表面受到空间旋转的非参数方法。实现这种方法的主要挑战在于，大多数脑图中没有数据的内侧壁可以旋转到皮层表面。这是一个重要的考虑因素，因为内侧壁旋转引起的数据丢失可能会使结果产生偏差。为了解决这个问题，研究人员选择要么舍弃缺失的数据，要么将最近的数据分配给缺失的区域，要么完全忽略内侧壁。其他研究小组设计了不依赖空间旋转而是使用生成模型的替代方法。这些参数化框架在其概念和数据生成过程的实现方面有所不同，包括从空间滞后模型到频谱随机化再到变异函数匹配。当这些不同模型应用于相同的实验问题和数据集时，它们的表现如何仍不清楚。

在这里，本文全面比较了十种已发表的零模型如何控制神经影像数据统计分析中的FWER。首先，通过全面模拟，本研究检查了每个零模型统计推断的准确性及其各自的假阳性率。然后，根据开源数据集(Neurosynth；Human Connectome Project)，将每个零框架应用于两种分析：(1)评估脑图之间的对应关系和(2)评估分区内特征的空间分布。在所有分析中，本研究系统地考察了分区对零模型性能的影响。

方法

代码和数据可用性

所有用于数据处理、分析和图表生成的代码均可在GitHub或Zenodo上找到(https://github.com/netneurolab/markello_spatialnulls；https://doi.org/10.5281/zenodo.3986111)，并直接依赖于以下开源Python软件包：BrainSMASH、BrainSpace、IPython、Jupyter、Matplotlib、NeuroSynth、NiBabel、NumPy、Pandas、PySurfer、Scikit-learn、SciPy和Seaborn。报告分析中使用的其他软件包括FreeSurfer(v6.0.0，http://surfer.nmr.mgh.harvard.edu/)和Connectome Workbench(v1.4.2，https://www.humanconnectome.org/software/connectome-workbench)。

零模型框架

在这里，本文简要介绍了最初在文献中提出的零模型框架，并解释了本报告中所使用的具体实现细节。有关概述请参阅表1和图1。

表1.零模型框架。实现所有框架的代码和/或参考代码可在https://github.com/netneurolab/markello_spatialnulls上获取。

图1.零模型框架示例。

朴素模型

在开发空间约束框架之前，所谓的朴素模型在构建零分布时没有考虑数据的空间结构，通常会导致整体错误率虚高。本研究测试了两个这样的朴素模型：一种是参数化方法，另一种是非参数化方法。

朴素参数法：虽然参数化方法的具体实现因所采用的统计检验而异，但所有实现都依赖于标准零分布。例如，在检查相关值时，参数化方法依赖于t分布；在检查z-统计量时，该方法使用标准正态分布。

朴素非参数法：朴素非参数方法利用数据的随机排列来构建零分布，破坏其固有的空间结构。每个顶点或区域在每次排列中都会被分配另一个顶点或区域的值。

空间置换模型

最早由Alexander-Bloch等人(2013)提出，后来在Alexander-Bloch等人(2018)的研究中正式发表，该模型通过对大脑的球形投影应用随机旋转来生成具有空间约束的零分布。将旋转矩阵(R)应用于大脑的三维坐标(V)，以生成一组旋转坐标(Vrot=VR)。通过将每个坐标的原始值替换为最近的旋转坐标值来构建置换。旋转是一个半球独立产生的，然后沿前后轴镜像到另一个半球。

将Alexander-Bloch旋转方法应用于分区大脑数据涉及几种方法的选择，近年来至少有四种对这种技术的不同改编已发表：Vázquez-Rodríguez等人(2019)，Váša等人(2018)，Baum等人(2020)和Cornblath等人(2020)。本研究测试了这四种改编方法，以及另一种其自然延伸的方法(Hungarian)。然而，需要注意的是，当分析顶点水平数据时，所有这些改编方法都归结为原始的Alexander-Bloch技术。

参数化数据模型

不同于Alexander-Bloch等人(2018)空间置换模型的构建，参数化数据模型不依赖于旋转来生成零分布。相反，这些模型生成保留了其估计数据特征的空间特征的替代零映射。本研究测试了三种这样的模型，这些模型最初被用于神经影像学(Burt-2018方法，Burt-2020方法)和生态学(Moran方法)研究中。

结果

零模型在模拟脑图上的性能

为了定量评估零模型在已知真实数据上的表现，本研究进行了一系列模拟。首先，直接采用Burt等人(2020)的方法，在七个不同的空间自相关性(α)上模拟了1000对来自高斯随机场(GRFs)的相关脑图(r=0.15)。本研究将每个零模型框架应用于每对脑图，以生成每对1000个零映射，每个空间自相关水平对应一百万个零映射。本研究使用这些零映射来生成关于脑图对之间原始相关性的双侧p值。

图2.模拟脑图上的零模型性能。

对模拟数据p值的检查显示，空间约束零框架(图2c；红线和蓝线)的性能大体相当。在较低水平的空间自相关性(α≤1.5)下，空间约束零模型与空间朴素模型的性能相当(图2c；紫线)；然而，在较高水平的空间自相关性(α＞1.5)下，空间约束零映射会产生更保守的统计数据。虽然对顶点水平脑图对进行分区会改变它们的相关结构，但分区结果与在顶点水平数据中观察到的结果一致。

接下来，为了研究零模型的假阳性率(FPR)，本研究从之前的分析中提取了模拟的脑图对，并对它们进行了混洗，得到成对的随机相关脑图。在低水平的空间自相关性(α≤2)下，随机脑图对之间的相关性分布紧密地集中在r=0.0；然而，随着空间自相关性水平的增加(α＞2)，相关性分布的方差显著增大(图2d)。也就是说，在高度空间自相关的情况下，两个随机选择的脑图更可能存在强相关性。为了测试零框架能否充分控制这种相关性分布的扩大，本研究重新将每个框架应用于所有随机化的脑图对，为每个框架生成一个p值分布。然后，评估给定框架p值小于0.05的概率(此时的p值相当于假阳性率；FPR)。

当数据中不存在空间自相关性(α=0.0)时，所有模型的表现相当，FPR约为5%；然而，随着空间自相关性的增加，模型的FPR各不相同(图2e)。不出所料，空间朴素模型很快达到了接近100%的FPR(图2e；紫线)，这与Burt等人(2020)的研究结果一致。更值得注意的是：在较高水平的空间自相关性(α≥2)下，所有空间约束零模型的FPR都有所增加(图2e；红线和蓝线)。在最高水平的空间自相关性下，即使是最保守的零模型也有大约13%的FPR(fsaverage5：13.5%；Cammoun：13.3%；Schaefer：13.1%)。此外，在这些较高水平的空间自相关性下，空间约束零模型族之间出现显著的差异，与空间置换模型相比，参数化数据模型具有更高的FPR。本研究发现空间自相关性对FPR的影响以及零模型之间的差异在不同分割分辨率上是一致的。还需要注意的是，在Burt-2020模型中，参数选择似乎会影响结果的FPR。

为了检查零模型性能之间的差异是否源于构建不良的零映射，本研究考察了每个框架生成的零映射如何有效地捕捉原始数据的空间自相关性。本研究计算了每个空间自相关性水平上10000个模拟脑图的Moran's I(图3a-d，左图)，并且对于每个空间自相关性水平的模拟，计算了由每个零模型框架生成的10000个零映射的Moran's I(图3a-d，右图)。

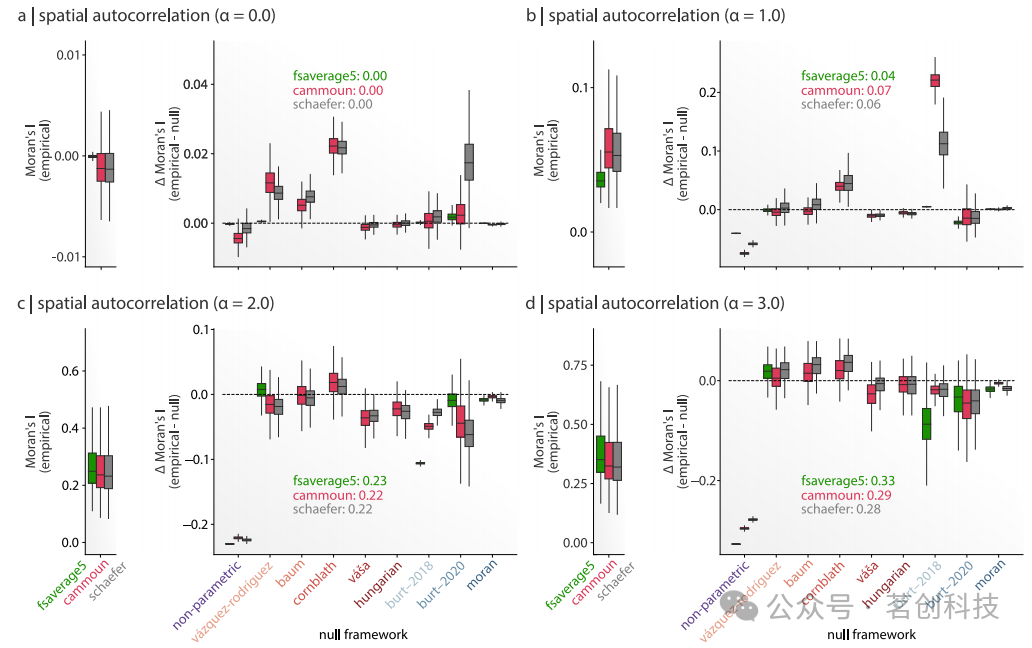
图3.零模型以不同方式保留模拟数据的自相关性。

模拟脑图的Moran's I在不同的空间自相关性水平(α)之间存在很大差异，但在顶点和分区数据之间的差异并不明显。另一方面，零映射的Moran's I似乎与框架和空间自相关性有关。在空间置换零模型框架中，本研究观察到方法性能上的普遍差异：与Vázquez-Rodríguez、Baum和Cornblath方法相比，Váša和Hungarian方法的表现更为相似。前者执行“完美”的排列，但以牺牲输入数据的相对空间方向为代价。而后者则试图更接近地保留空间方向，但会稍微改变底层数据分布。有趣的是，由Moran框架生成零映射的Moran's I统计数据(该框架旨在使零映射明确匹配输入脑图的Moran's I)可能与所有零模型的输入脑图最接近；然而，正如先前观察到的那样，Moran方法的FPR仍明显高于所有空间置换框架的FPR(见图2e)。这种差异表明，最佳信号检测可能不仅取决于匹配空间自相关性，还可能取决于匹配输入脑图的其他特征，包括高阶相关性或空间非平稳性。

测试脑图之间的对应关系

接下来，研究了零模型在应用于神经影像数据集的两个典型分析中的表现。本研究首先考察了十种零模型在测试元分析功能激活之间相关性时的表现。按照Alexander-Bloch等人(2018)的方法，将源自NeuroSynth的123个认知术语进行元分析“关联”图的划分。使用特定术语的关联图来构建一个术语×术语的线性相关矩阵，表示成对术语共享相似空间模式的程度(见图4a)。然后，应用每个零模型来生成一组术语×术语相关矩阵(见图4b)。最后，通过保留每个术语×术语矩阵中的最大绝对相关系数(排除对角线元素)来构建一个零分布(见图4c)。该过程为每个零模型生成零相关分布，用于阈值化术语×术语相关矩阵。

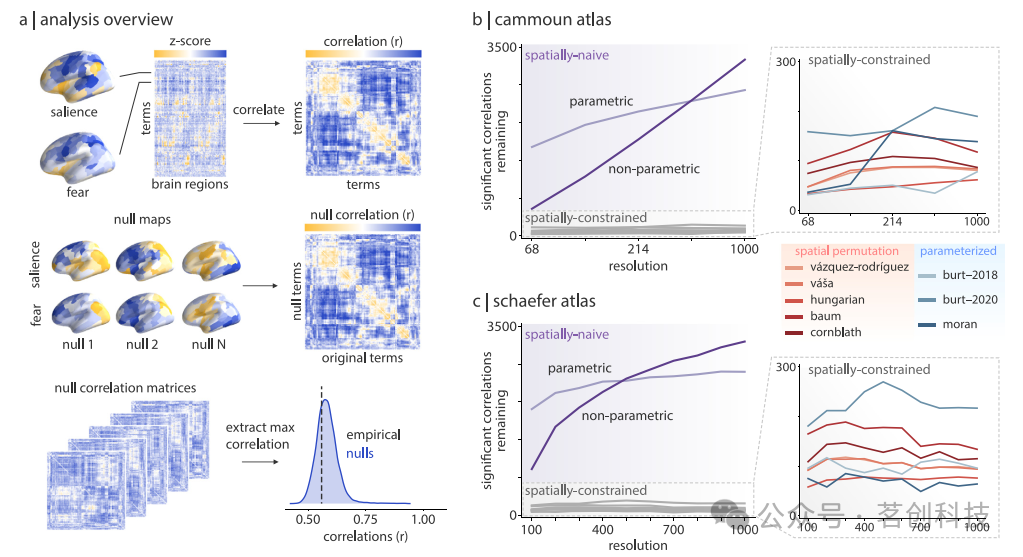
图4.测试脑图之间的对应关系。

图4b、c显示了阈值化后，在术语×术语矩阵中保留的具有显著相关性的数量。所有比较均在p≤0.05下进行。为了测试零模型和分割分辨率之间的交互作用，本研究突出显示了Cammoun和Schaefer分区的所有分辨率(Cammoun图谱的分辨率为5；Schaefer图谱的分辨率为10)下的结果。

总的来说，零模型之间存在显著差异。与模拟分析结果相似，参数化和非参数化的空间朴素模型都产生了不切实际的宽松结果。在空间约束零模型中，一些方法略微宽松，产生了更多的显著相关性(例如Burt-2020，Váša)，而其他方法始终较为保守(Burt-2018，Cornblath)。此外，尽管零模型之间存在差异，但零模型的相对顺序在多个分割图谱和分辨率上是稳定的，这表明模型在不同节点定义下的表现一致。

测试分区特异性

接下来，在分区特异性测试中比较零模型，检查空间特征(例如，皮层厚度、皮质髓鞘、功能连接强度)是否明显更集中于感兴趣的分区(如特定的内在功能网络或细胞结构类)。具体而言，本研究测试了T1w/T2w比值(该比值被认为反映了皮层髓磷脂的变化)的空间分布是否受到内在功能或细胞结构网络边界的限制。

本研究首先计算了Yeo等人(2011)七个网络中所有分区的平均T1w/T2w比值(图5a)。然后，使用每个零模型来生成特定网络的T1w/T2w均值的分布。最后，将每个实际网络均值表示为相对于其各自零分布的z分数。通过计算绝对零网络均值大于绝对实际网络均值的比例来估计特定网络的p值，量化了T1w/T2w比值在特定网络中显著大于或小于网络大小、对称性等的概率(图5a)。

图5.测试分区特异性。

图5b、c显示了特定于网络T1w/T2w比值的z分数。具有统计显著性(双侧，p≤0.05)的典型网络平均T1w/T2w比值用红色表示，而不显著的网络用灰色表示。本研究对Cammoun和Schaefer图谱的所有分辨率重复了这些比较。

本研究观察到三大趋势。首先，零模型在效应方向和网络z分数的相对排序方面基本一致：大多数方法识别出感觉运动和视觉网络中T1w/T2w比值的过表达，而在腹侧注意、默认、额顶叶和边缘网络中表达不足(图5b、c)。其次，尽管存在这些相似之处，但不同零模型在它们提供的统计推断方面并不一致：显著网络的数量和特性因模型而异。第三，这些模型在保守程度上是可变的。与使用NeuroSynth数据得到的结果相比，不同模型之间的差异似乎在很大程度上取决于模型族，空间置换零模型往往更为保守(Vázquez-Rodríguez、Baum、Cornblath)，参数化零模型更为宽松(例如Burt-2018和Burt-2020)。模型族之间的这些区别在每个框架生成的零分布形状上也很明显。

区域质心定义的变异性

在本文所提出的五个空间置换零模型中，有三个需要为每个区域定义一个质心(Vázquez-Rodríguez、Váša和Hungarian)。区域质心是按照Vázquez-Rodríguez等人(2019)使用的程序生成的，包括：(1)取给定区域内所有顶点坐标的平均值，(2)使用最接近该平均值的表面顶点的坐标(其中最接近被定义为最小化欧氏距离)。然而，Váša等人(2018)仅使用每个区域内顶点的平均值来定义其区域质心(即不投影回表面顶点)。值得注意的是，这两个步骤都未考虑其质心可能落在区域边界之外。考虑到这种可能性的一种解决方法是找到顶点坐标，使到每个区域内所有其他顶点的平均表面(测地线)距离最小。

本研究评估了这三种区域质心定义方法对三个相关零模型旋转的影响程度。本研究生成了十个旋转矩阵，并将它们应用于由这三种区域质心定义方法得到的坐标上，使用每个相关零框架的方法重新分配区域。使用标准化汉明距离(图6a)比较重新分配的相似性。关键是，由于每个模型和方法都应用了相同的旋转，因此任何观察到的差异都是区域质心坐标或模型本身变化的结果。

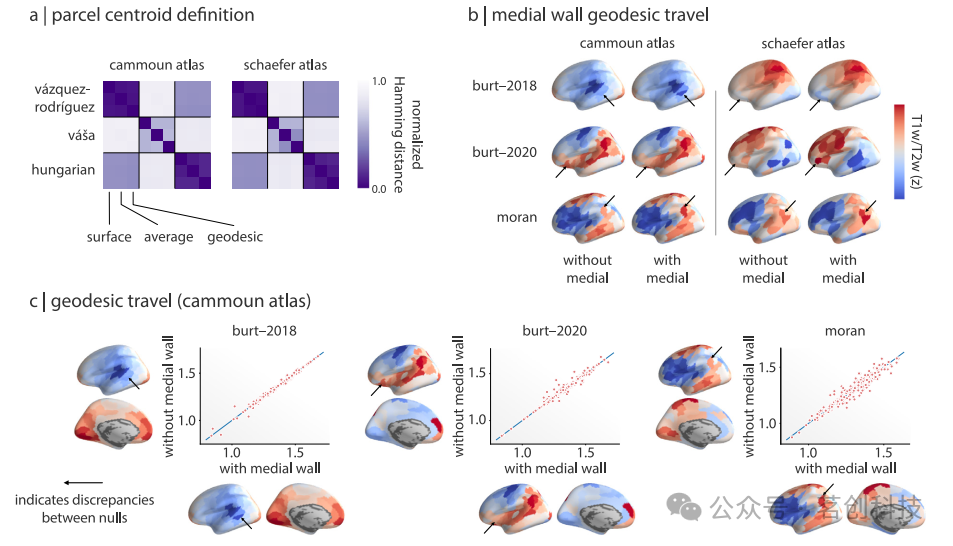
图6.零模型对性能的影响。

图6a显示了在Cammoun和Schaefer图谱(分别为219-200个节点)之间，使用这些区域质心和零框架方法的所有组合重新分配之间的汉明距离。可以观察到，不同零模型方法生成的重新分配之间存在的最大差异。特别是，Váša的零模型方法似乎与Vázquez-Rodríguez和Hungarian方法明显不同。此外，区域质心计算方法也存在差异；例如，Váša方法似乎在不同的区域质心定义之间只有适度的对应关系。这些结果不仅突显了空间置换零模型之间的重要差异，而且还突显了每个模型实施本身的差异。

结论

本研究综合分析了神经影像研究中用于比较脑图的10种零模型。研究结果发现，相较于空间朴素模型，考虑空间自相关性的零模型的性能显著提高，错误率降低；然而，在所有分析中，空间约束零模型之间可能存在有意义的潜在差异。本研究结果强调了需要仔细考虑这些零模型方法实施过程中的差异，并在更广泛的研究背景下比较它们的性能。

参考文献：Ross D. Markello, Bratislav Misic, Comparing spatial null models for brain maps, NeuroImage, Volume 236, 2021, 118052, ISSN 1053-8119, https://doi.org/10.1016/j.neuroimage.2021.118052

 小伙伴们关注茗创科技，将第一时间收到精彩内容推送哦～