滤波、卷积、互相关和内积之间的关系

首先，滤波就滤波，为什么叫卷积？不就线性组合吗？

1. 空域滤波是一种邻域或非局部处理。滤波最初是频域的概念。

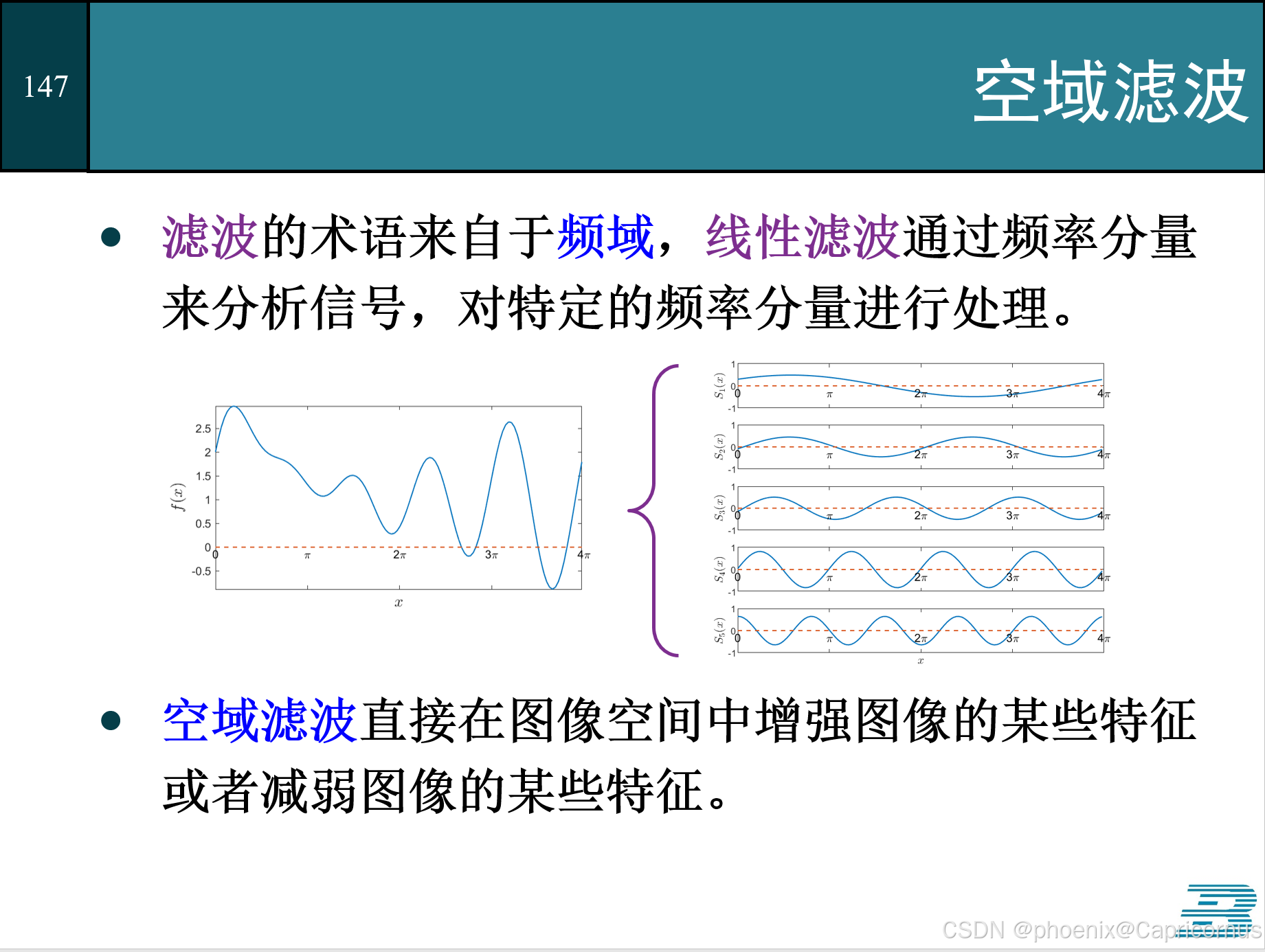
2. 由于频域乘积对应空域卷积，所以在空域就用卷积实现。

3. 卷积也就是线性组合。
   
   

4. 在图像处理中反转没必要，设计系数时转了就行，然后就成了互相关。实际理解也是模板匹配。mask和template中文都翻译为模板（掩膜的翻译不说人话），小的模板叫mask，大的就叫template。
   
   

5. 卷积就这么来了。线性空域滤波与卷积有对应关系，不是空域滤波都能用卷积实现。但是非线性滤波也用滤波这个专业术语了。

附：模板匹配

卷积（Convolution）

定义：卷积是一种数学运算，它将两个函数（例如，一个信号和一个滤波器）合并成一个新的函数。在信号处理中，卷积通常用于对信号进行滤波，以改变信号的频率特性或去除噪声。在图像处理中，卷积常用于特征提取和边缘检测等任务。

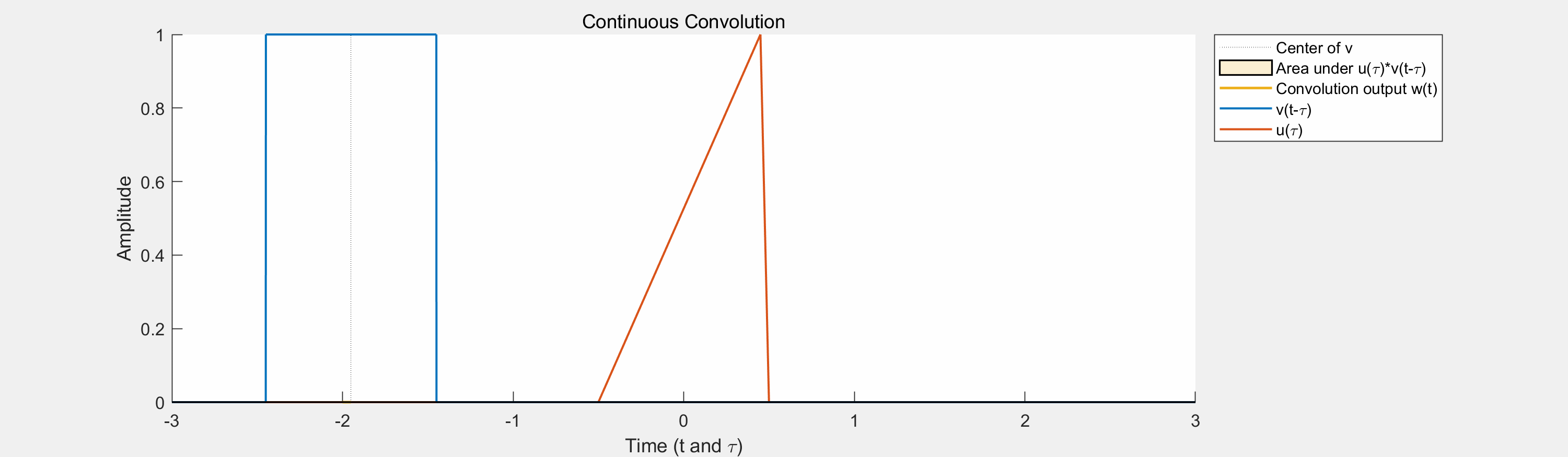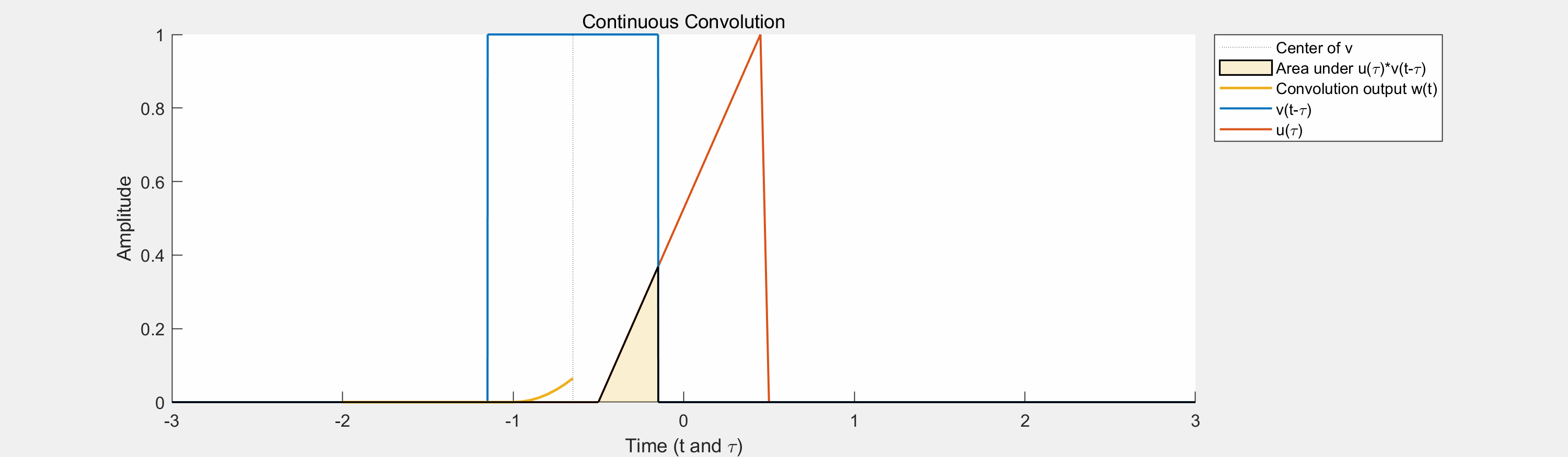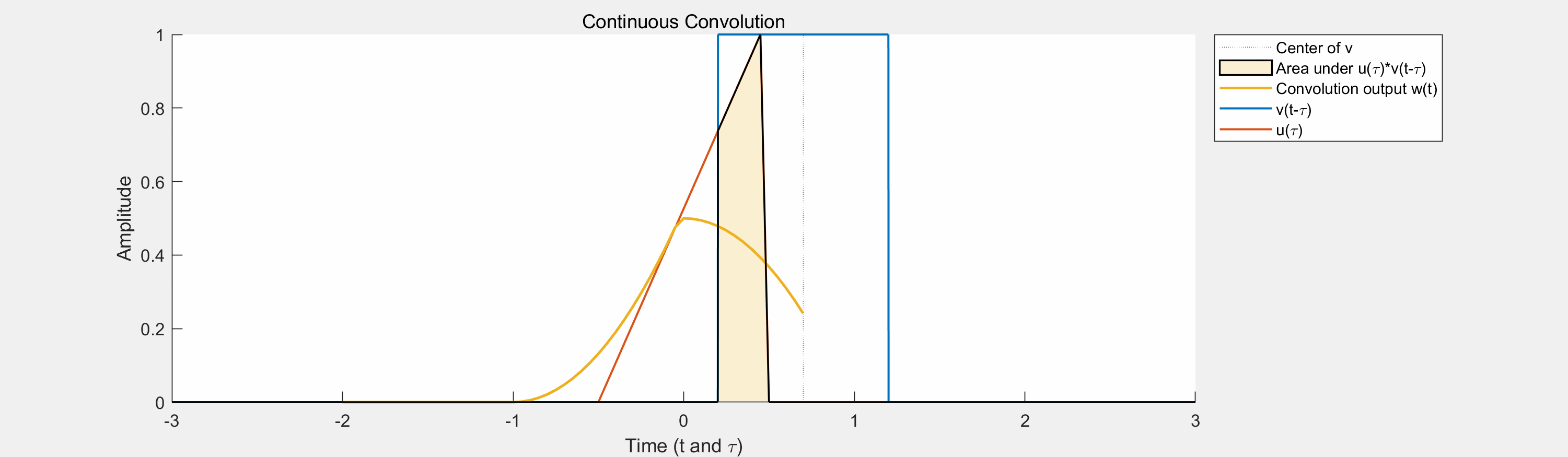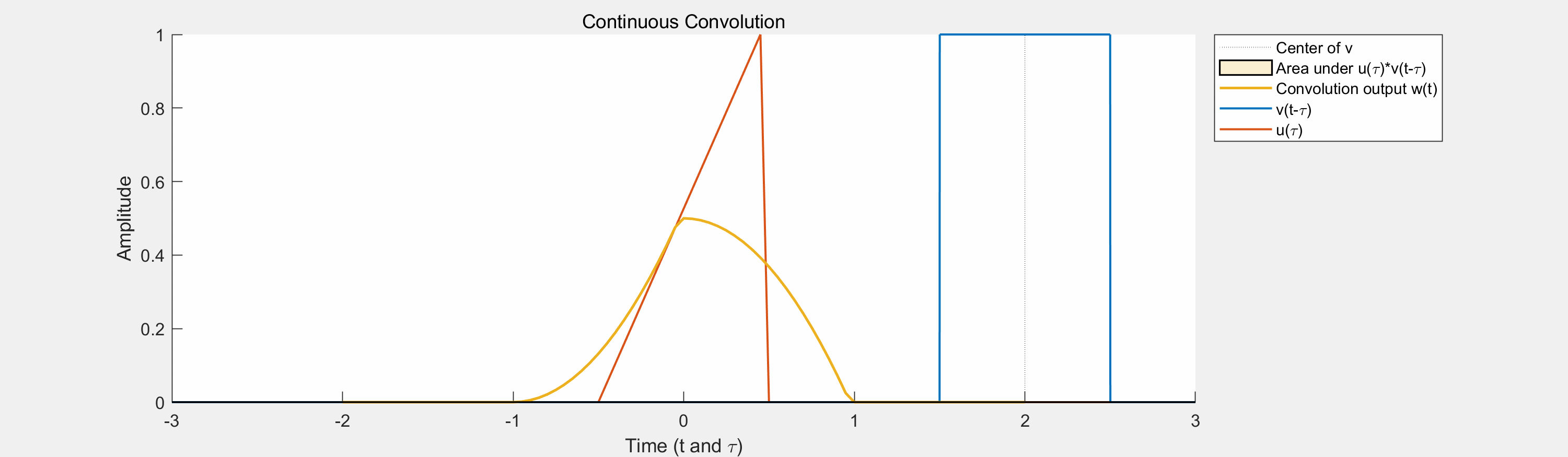
与滤波、互相关的关系：

• 卷积操作涉及两个函数的相对位移和乘积的积分（或求和，对于离散信号）。
• 由于卷积定理表明，频域滤波等效于空域卷积，因此，滤波利用卷积实现。
• 然而在深度学习中，卷积神经网络（CNN）中的卷积操作通常是对输入图像和卷积核（即滤波器）进行滑动窗口的内积（也称为点积）求和，但这里的“卷积”实际上是互相关操作。这是因为卷积和互相关就差一个核的反转，网络直接学习滤波器，反不反转没有关系。另外，CNN中卷积层的实际意义正是互相关的意义。其实应该称为互相关神经网络。

滤波（Filtering）

定义：滤波是一种信号处理技术，用于改变信号的频率特性。滤波器是一种能够执行这种操作的电路或算法。滤波器的种类很多，如低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。

与卷积的关系：

• 滤波器通常通过卷积运算与信号进行交互，以改变信号的频率特性。因此，卷积是滤波操作的基础。
• 在数字信号处理中，滤波器通常被表示成离散时间函数的形式，而卷积则是将信号与滤波器进行卷积运算的方法。

互相关（Cross-Correlation）

定义：互相关是两个函数之间的相似度度量，它描述了一个函数相对于另一个函数位移时的相似程度。在信号处理中，互相关常用于检测信号中的延迟或相似特征。

与卷积的区别：

• 卷积操作涉及滤波器的反转和位移，而互相关则不涉及滤波器的反转。
• 从数学上看，互相关可以看成两个函数之间的滑动内积，而卷积则是反转后的滑动内积。

在深度学习中的应用：

• 在深度学习中，尤其是在卷积神经网络中，由于卷积核通常不反转，因此实际的卷积操作是互相关。

内积（Inner Product）、点积

定义：内积是线性代数中的一个概念，它定义了向量空间中两个向量的点积。在函数空间中，内积可以定义为两个函数乘积的积分（或求和，对于离散函数）。

与互相关的关系：

• 互相关运算可以看作是在不同位移下对两个函数的内积。
• 在某些情况下，互相关可以表示为内积，即卷积核（互相关运算的核也称为卷积核）在信号上滑动时，每个位置的互相关值可以看作是该位置处信号与卷积核的内积。

总结

• 卷积与滤波 卷积是滤波操作的基础，它通过两个函数的相对位移和乘积的积分来合并这两个函数。
• 滤波与卷积 滤波用于改变信号的频率特性，通常通过卷积运算实现。
• 互相关与卷积 互相关和卷积的不同在于，不涉及滤波器的反转，常用于检测信号中的相似特征。
• 内积与互相关 内积是线性代数中的概念，用于度量向量之间的相似度，互相关运算可以看作是在不同位移下对两个函数的内积。