【图文详解】如何降低Transformer的计算复杂度：Transformer架构原理和改进自注意力机制

已于 2023-07-12 14:55:27 修改
阅读量865 收藏 5
点赞数 3
分类专栏： DeepSeek R1 & 大数据AI人工智能大模型 ChatGPT 文章标签： 自然语言处理 人工智能 语言模型 编程实践 开发语言 架构设计
于 2023-07-12 01:20:38 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/universsky2015/article/details/131672259
版权
本文详细分析了Transformer计算复杂度，重点探讨了自注意力机制的计算过程，包括矩阵计算、注意力矩阵归一化和加权求和。针对自注意力层的高计算复杂度，提出了稀疏化和线性化两种改进策略，介绍了包括Sparse Transformer、Reformer、Linformer等在内的多种优化方法，旨在降低长序列处理时的计算成本。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

文章目录

如何降低Transformer的计算复杂度

Efficient Transformers.

本文目录：

  1. Transformer的计算复杂度
  2. 改进自注意力机制

1. Transformer的计算复杂度

(1) Transformer的典型结构

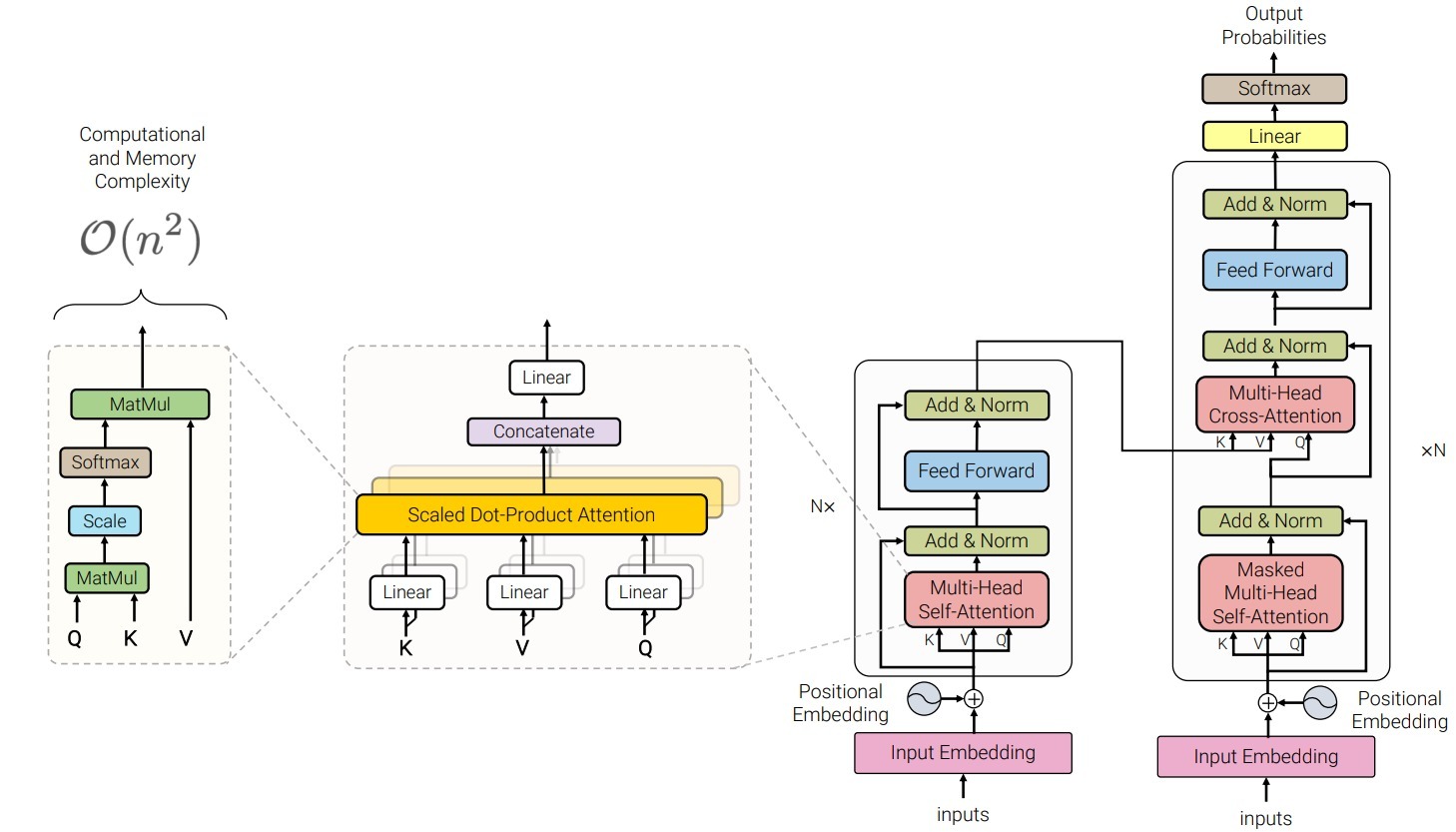
典型的Transformer结构如上图所示，其整体计算量来源于模型中的自注意力层和全连接层两部分，本文主要讨论自注意力层的改进。

(2) 自注意力机制的运算

由于计算机中乘法的计算速度比加法慢，因此在衡量计算复杂度时主要考虑乘法。对于矩阵乘法

了解本专栏 订阅专栏 解锁全文 超级会员免费看
ResNet改进(2)：添加Transformer注意力
2401_82355416的博客
03-11 830
注意力模块（Attention Module）是深度学习中一种重要的机制，旨在让模型在处理输入数据时能够动态地关注最重要的部分。它最初在自然语言处理（NLP）领域被提出，并逐渐扩展到计算机视觉、语音识别等多个领域。
Transformer 工作原理图文详解和实践：在生成式对话系统中的核心技术剖析
AI天才研究院
04-04 731
生成式对话系统是自然语言处理领域的一个重要研究方向,它旨在通过机器学习的方式,让计算机能够自动生成人类可读的、连贯有意义的对话回复。在过去的几年里,基于深度学习的生成式对话系统取得了长足的进步,其中Transformer模型凭借其强大的序列建模能力,在生成式对话系统中发挥了关键作用。
分层级联Transformer！苏黎世联邦提出TransCNN: 显著降低了计算/空间复杂度！
深度学习技术前沿
06-11 1882
导读本文是苏黎世联邦理工-Luc Van Gool组联合南开大学和电子科技大学在Transformer上的最新工作，这项工作主要提出了一个新的分层级联多头自注意力模块(MHSA)，通过分...
Transformer参数量和复杂度
qq_45978862的博客
09-01 1197
在算法岗面试中经常会问到Transformer相关的基础知识。首先需要清楚Transformer的参数量和复杂度分别在算什么。其他部分包括Input Embedding 、Postion Encoding以及最后解码的Linear层。其中，每个MHSA、Masked MHSA、Multi-Head Cross-Attention和FFN中有含有Add&Norm操作。
【Transformer改进】解决Transformer复杂度较大问题的变体模型Star Transformer
这个博客太懒了什么都没说
01-12 678
【文献分享】解决Transformer复杂度较大问题的变体模型Star Transformer
AI之Transformer：Transformer算法原理探索之基于 Transformer 模型层的中间层表示空间及其对计算效率的影响之实证研究
头部AI社区如有邀博主AI主题演讲请私信—心比天高，仗剑走天涯，保持热爱，奔赴向梦想！低调，专注，谦虚，自律，反思，成长，还算比较正能量的博主，公益免费传播…内心特别想在AI界做出一些可以推进历史进程影响力的技术(兴趣使然，有点小情怀，也有点使命感呀
07-24 1878
​ AI之Transformer：Transformer探索之基于 Transformer 模型层的中间层表示空间及其对计算效率的影响之实证研究 目录 相关文章 基于 Transformer 模型层的中间层表示空间及其对计算效率的影响之实证研究 相关文章 《Transformer Layers as Painters》翻译与解读 地址 论文地址：https://arxiv.org/abs/2407.09298v1 时间 2024年7月12日 作者 Q
Transformer模型的时间复杂度
热门推荐
争渡的博客
05-05 2万+
模型的时间复杂度主要取决于输入序列的长度N和模型中隐藏层的数量H。对于一个具有L个层的模型，其时间复杂度为O(LN^2H)，其中N ^2来自于注意力机制的计算。因此，对于较长的输入序列和更深的模型，的时间复杂度可能会非常高。这里表示算法的时间复杂度是O(LN ^ 2H)，其中LNH是三个参数。在这个算法中，输入的规模为L，每个输入的处理需要O(N ^ 2)的时间，一共要进行H次处理。因此，总的时间复杂度就是O(LN^2H)。H代表中多头注意力机制的数量。N代表输入序列的时间步长，也就是序列的长度。L。
【图像去噪】论文复现：新型Transformer块！可学习扩张卷积用于噪声估计引导多头自注意力！AKDT的Pytorch源码复现，跑通源码，获得去噪结果和评价指标，网络结构实现详解，并计算模型复杂度！
最新发布
主要更新底层视觉（去噪、超分等）相关的科研内容，形式为【论文精读】+【论文复现】
03-25 1112
论文题目：AKDT: Adaptive Kernel Dilation Transformer for Effective Image Denoising —— AKDT:用于有效图像去噪的自适应核膨胀Transformer【图像去噪】论文精读：AKDT: Adaptive Kernel Dilation Transformer for Effective Image Denoising本文以真实去噪SIDD数据集为例进行复现。
精确率与深度学习:自注意力与Transformer
AI天才研究院
06-27 642
在人工智能领域，深度学习模型的精确率一直是研究者们追求的目标。近年来，随着计算能力的提升和数据的爆炸式增长，深度学习在图像识别、自然语言处理、机器翻译等领域取得了突破性进展。然而，传统的深度学习模型，如循环神经网络（RNN）和卷积神经网络（CNN），在处理长序列数据时往往会遇到瓶颈，例如梯度消失或爆炸、难以捕捉长距离依赖关系等问题。为了解决这些问题，研究者们不断探索新的模型和算法。
自注意力(SelfAttention)原理与代码实战案例讲解
AI天才研究院
06-18 743
自注意力(Self-Attention)是一种用于自然语言处理(NLP)和计算机视觉(CV)等领域的技术，它可以帮助模型更好地理解输入数据中的关系和重要性。自注意力最初是在Transformer模型中提出的，而Transformer模型则是目前NLP领域最先进的模型之一。自注意力的应用已经被广泛应用于各种任务，例如机器翻译、文本分类、语音识别、图像生成等。自注意力机制的核心思想是让模型在处理一个输入序列时，能够对序列中的每个元素进行加权求和，从而捕捉到序列中元素之间的关系。
Transformer 的结构改进与替代方案
hellozhxy的博客
03-09 3438
自从 Transformer 结构被提出以来，以 BERT 为代表的 Encoder 模型，以 GPT 为代表的 Decoder 模型，以 ViT 为代表的 CV 模型，都烜赫一时。时至今日，几乎所有的 LLM 也都是 Transformer 结构，尽管不时也会有新的结构被提出来，但 Transformer 的江湖地位仍然无可撼动。希望通过以上问题的思考和讨论，能够帮助我们更好地使用Transformer、理解Transformer、优化Transformer和改进Transformer。
SwinTransformer 改进：添加SelfAttention自注意力层
Henry的博客
12-22 366
Self-Attention自注意力层是一种在神经网络中用于处理序列数据的注意力机制。它通过对输入序列中的不同位置进行关注，来计算每个位置与其他位置的关联程度，并根据这些关联程度对输入序列进行加权。自注意力层的优势在于它能够利用序列中的局部和全局信息，从而更好地捕捉序列中不同位置之间的依赖关系。在自然语言处理领域中，自注意力层被广泛应用于机器翻译、文本分类和阅读理解等任务中。输出size：torch.Size([1, 10])添加如下：其中sa部分就是添加的模块。想要完整的分类代码，请参考。
transformer系列之时间复杂度
ningyanggege的博客
11-08 5590
假设我们有两个矩阵，A的维度为(m x n)，B的维度为(n x p)，则结果矩阵C的维度为(m x p)对于结果矩阵C中的每个元素，我们需要计算矩阵A中的一行和矩阵B中的一列的点积。这个点积涉及到对应元素的乘积和求和。为了计算C中的每个元素，我们需要执行n次乘法和n-1次加法，如果再加上偏置项，刚好就是2*n由于结果矩阵C中有m x p个元素，因此所需的总操作数为(m x p) x 2 x n。但为了表述简洁性，忽略细节，可以写成mp2*n。
降低Transformer复杂度O(N^2)的方法汇总
idol24的博客
12-19 872
作者丨Civ@知乎 编辑丨极市平台来源丨https://zhuanlan.zhihu.com/p/634406691Transformer最重要的特性是Global Interaction，也就是说对于任意两个位置的token（不论它们离的有多远），它们之间都能直接进行信息交互。这个特性解决了传统序列建模中长依赖的问题。但Transformer也有一个典型问题：它的计算复杂度和空间复杂度均为 ...
深度学习|transformers的近期工作成果综述
renhongxia1的博客
10-19 492
作者提出了一种基于自监督的视觉表示模型，即来自图像transformer的双向编码器表示(BEiT)，它遵循了为自然语言处理领域开发的BERT [Kenton 2019]方法。ViT特征包含低层信息，对对抗攻击提供了优越的鲁棒性，并指出与增加尺寸或增加层数的纯transformer模型相比，cnn和transformer的组合具有更好的鲁棒性。Liu等人[Liu 2021]讨论了transformer从语言领域到视觉领域的适应问题，方法包括大量视觉实体的差异和与文本中的文字相比的图像的高分辨率像素差异。
Transformer模型-矩阵乘法；与点积 dot product（点积相似度 dot product Similarity）的关系；计算attention
Ankie资深技术项目经理
03-29 992
Ankie的评论：因为点积可以计算相似值，或者距离，attention就拿来计算attention的相似值，或者距离。两个向量a = [a1, a2,…3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。1、当矩阵A的列数（column）等于矩阵B的行数（row）时，A与B可以相乘。Ankie的评论：一个人是站着的，一个人是躺着的，站着的高度=躺着的长度。矩阵C的第一个元素，其实就是A的第一行和B的第一列做点积。2、矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。
为什么Transformer在训练时需要如此多的算力，是否有理论解释？
11-26 184
Transformer模型由于其卓越的表现，广泛应用于自然语言处理、计算机视觉等领域。然而，这种模型在训练时往往需要消耗巨大的计算资源，尤其是在面对大规模数据集和复杂任务时，计算需求呈指数增长。
不得不看！降低Transformer复杂度的方法
Kaiyuan_sjtu的博客
03-28 5655
作者|Chilia整理|NewBeeNLP首先来看一下原始Transformer的复杂度self-attention复杂度记:序列长度为n，一个位置的embedding大小为d。例如(32,512,768)的序列，n=512，d=768.首先，得到的QKV都是大小为 的。相似度计算 : 与 运算，得到 矩阵，复杂度为softmax计算: 对每行做s...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

AI天才研究院

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值