【读论文09】-时空预测-STGCN - SBAS-InSAR

【读论文09】-时空预测-STGCN-SBAS-InSAR

摘要

开门见山 引出主题
准确预测滑坡对于有效预警和管理至关重要，但由于触发事件的不可预测性以及土壤和坡体结构的空间异质性，这一任务仍然具有挑战性。
引出问题
现有预测方法通常依赖点采样数据，忽略了滑坡演化中的异质性。
本文方法
为此，我们提出将时空图卷积网络（STGCN）与合成孔径雷达干涉测量（InSAR）相结合，以捕捉滑坡事件的时空特征。STGCN 通过图神经网络（GNN）层处理空间特征，并利用门控循环单元（GRU）层分析时间动态，从而更精确地提取与滑坡相关的位移特征。
结果与结论
我们在中国青藏高原金沙江色拉山地区应用该方法，结果表明，与传统深度学习模型相比，STGCN 模型显著提高了预测精度，其均方误差（MSE）和平均绝对误差（MAE）分别降低至 25.51 和 2.34，相较于最佳传统模型提升了 35% 和 50%。值得注意的是，该方法首次在滑坡预测中纳入了物质迁移方向的考虑，有效应对了空间异质性问题，并将预测框架从单纯的时间维度拓展到时空双维度。研究结果表明，这一集成方法为更准确、全面的滑坡预测提供了一种强有力的工具。

引言

1. 研究背景与现有方法
• 滑坡预测方法：现有长期（数月到数年）滑坡预测方法主要分为三类：
• 数学模型（简单直接，但难以处理复杂现实数据）；
• 机器学习（擅长模式识别，依赖参数调优）；
• 物理模拟（需大量数据，如位移、水位、降雨等）。
• 关键问题：现有方法多依赖点采样数据，难以捕捉滑坡的时空异质性（如材料、结构差异导致的蠕变、断裂等动态变形模式）。

2. 研究挑战与解决思路
• 核心挑战：点采样数据无法全面反映滑坡的三维时空动态，导致预测精度受限。
• 解决方向：需结合全滑坡变形历史反演和时空特征提取，实现“滑坡全景预测”（LPP）。
• 技术路径：
• InSAR（干涉合成孔径雷达）：高精度追踪历史位移；
• 深度学习（如ConvLSTM、HLSTM）：分析非线性时空关联，但现有方法对时空特征提取不足。

3. 本文创新点
提出STGCN（时空图卷积网络）与SBAS-InSAR协同框架，以解决时空特征建模问题：

1. 数据获取：利用SBAS-InSAR监测西藏色拉滑坡（2014–2022），结合无人机与实地验证分析运动特征。
2. 模型设计：STGCN提取变形场的复杂时空特征，结合自相关分析和高斯过程插值。
3. 验证对比：与4种基准方法对比，证明STGCN的优越性。
4. 深入分析：探讨时空权重参数和模型结构对预测性能的影响。

4. 主要成果

1. 构建长期位移监测时间序列；
2. 揭示滑坡运动学演化规律；
3. 提出STGCN-InSAR协同方法；
4. 验证时空特征对提升预测效能的关键作用。

---

引出话题
滑坡的长期预测（跨度为数月至数年）方法通常可分为三类：数学模型（Gao 等, 2021）、机器学习（Wang 等, 2021a; Wang 等, 2022; Zhu 等, 2022）和物理模拟方法（Lee 等, 2020; Wei 等, 2021）。数学建模通常较为直观，并能在特定数据集上表现良好，但在捕捉真实世界滑坡数据的复杂性和变异性方面存在困难（Hill 等, 2021; Huang 等, 2021）。物理模拟方法虽然有望生成可靠的结果，但需要大量数据输入，包括位移、水位、降雨、孔隙水压力和地下应力等，以实现准确预测（Ceccato 等, 2024; D’Ippolito 等, 2023; Shan 等, 2022）。

传统的机器学习或深度学习方法在模式识别和预测能力方面表现出色，它们通过从数据集中提取特征，并优化称为“参数”或“权重”的数值来进行训练（Liu 等, 2022a）。尽管滑坡预测方法多种多样，但许多现有研究的一个客观局限性在于依赖点采样数据。这主要源于滑坡全景数据长时间序列的稀缺性以及数据处理的困难。事实上，环境要素与坡面变异单元之间的复杂动态相互作用影响着滑坡的演化，这一现象已在多项研究中得到认可（Chen 等, 2024; Chen 和 Song, 2023; Fan 等, 2019; Kong 等, 2023）。这些因素在不同时间和地点影响滑坡演化，并受不同的坡面材料和结构影响。因此，不同的变形模式如蠕变、拉张破裂、褶皱和滑移等相继出现，反映了滑坡过程的时空异质性（Bao 等, 2023; Fan 等, 2017; Zhu 等, 2021; Zhuang 等, 2018）。然而，仅依赖采样点无法全面捕捉滑坡的时空动态，这往往导致对坡体材料和结构空间异质性的忽视。由于这种固有的复杂性，现有方法在准确建模滑坡的三维变形方面仍面临挑战。
引出监测工具（InSAR）
克服采样点局限性并实现滑坡全景预测（Landslide Panorama Prediction, LPP）的关键在于反演整个滑坡的综合变形历史，并从整体历史数据中提取时空特征以用于预测。深度学习作为机器学习的一个分支，在分析复杂、高度非线性和变化数据集的时间关联方面表现出色（Kim 和 Yun, 2024; Liu 等, 2022b）。干涉合成孔径雷达（InSAR）是一种稳健的方法，可用于追踪滑坡变形历史，结合深度学习可为滑坡位移的整体预测提供有前景的解决方案（Ge 等, 2024; Li 等, 2023a; Liu 等, 2022d; Mondini 等, 2021）。
已有的研究方法
卷积长短时记忆网络（ConvLSTM）（Yao 等, 2023）和异构长短时记忆网络（HLSTM）（Liu 等, 2021a）是两个典型案例，它们结合 InSAR 进行地表变形和大规模地面沉降的全景预测，并展现出卓越的准确性。然而，这些研究虽然认识到了时空特征的重要性，但并未对其进行深入剖析。ConvLSTM 试图通过对邻近点的卷积模糊地融入空间特征，这种方法适用于一维地面沉降，但在三维滑坡变形预测中遇到了挑战。而 HLSTM 认为空间特征隐含于时间序列数据中，这一假设可能难以被完全接受。截至目前，尚无研究能够真正从整体历史数据中提取时空特征并用于预测。
本文方法
鉴于当前研究的局限性，我们提出了一种有效解决方案，即将混合深度学习模型——时空图卷积神经网络（STGCN）与小基线集 InSAR（SBAS-InSAR）相结合。具体而言，SBAS-InSAR 被用于跟踪中国西藏贡觉县色拉滑坡自 2014 年 10 月 12 日至 2022 年 4 月 29 日的位移情况。随后，结合实地调查和无人机（UAV）测绘数据分析滑坡的位移特征、运动演化过程及潜在成因。在 LPP 方面，我们构建了 STGCN 的基础架构，以提取变形场的复杂时空特征。该方法结合了 InSAR 和 STGCN，考虑了滑坡位移过程的非线性特性，并采用自相关分析和高斯过程插值等方法进行融合。

为了验证 STGCN 的优越性能，我们设立了四种基准方法，并在相同条件下进行严格对比实验。结果表明，该融合方法在滑坡预测领域相较于基准方法表现出更高的预测效能。值得注意的是，本研究首次将坡面物质迁移的空间特征纳入滑坡预测框架。此外，为深入探讨时空特征在 LPP 中的作用，我们对 STGCN 在不同时空权重参数配置及不同模型结构配置下的表现进行了对比分析。研究最终得出了四个主要成果：

1. 长时序位移监测；
2. 滑坡运动学演化及位移特征分析；
3. STGCN 与 InSAR 协同方法的提出；
4. 证明 STGCN 在利用时空特征提升预测效果方面的能力。

2. 研究区域与材料

2.1 研究区概况

地理位置与地质背景
• 研究区位于中国西藏昌都市贡觉县，地处金沙江缝合带（JRSZ）东南缘，该构造带是松潘-甘孜地块、义敦地块和昌都地块的边界（图1a）。
• 地震活动：2012年以来，JRSZ共记录205次地震，其中：
• ≥5级地震9次（最高6.1级），
• 4~5级地震31次，震源深度最大达20公里（Liu et al., 2021c）。

地形与气候特征
• 地形：受金沙江侵蚀和复杂地质作用影响，地表崎岖破碎（Li et al., 2020; Zhan et al., 2018）。
• 气候：
• 气温：年均2~7°C，
• 降水：年降水量约500毫米，集中在6~9月。
• 植被：覆盖稀疏，以地衣、苔藓和灌木为主。

地层与岩性
• 主要地层（图2a）：
• 元古界、下三叠统，
• 金沙江超基性岩带，
• 石炭系-二叠系、中下更新统。
• 主要岩石类型：
• 雄松片麻岩群、英安岩、二长花岗岩，
• 石英二长玄武岩、安山岩、砂岩，
• 闪长岩、角闪岩、矽线石、蛇纹岩。

断裂构造
• 发育四条主要断裂（F1–F4），其中**雄松-索瓦隆断裂（F3）**规模最大，横穿研究区。

---

2.2 现场调查

2023年4月，研究团队对色拉山坡（图1b）开展了现场调查和无人机摄影测量。调查发现坡面广泛分布云母片岩碎屑，表明该区域风化作用强烈。色拉山坡呈舌状形态，坡向126°，长约3112米，宽2056米，相对高差693米，平面面积约4平方公里，前缘直抵金沙江（图1b）。坡体呈现中部平缓、上下陡峭的特征，整体坡度30°-35°，局部达40°-45°。

地质特征

1. 表层组成：以坡积物为主，局部基岩出露；
2. 基岩性质：雄松群云母片麻岩（图1c），具片状变质结构，属弱变质岩类；
3. 构造特征：
   • 坡顶和坡脚可见基岩露头，产状131°∠24°-171°∠83°，显示为顺向坡；
   • 发现两条断裂（F1、F2），对应地质图中的雄松-索瓦隆断裂，可能为逆断层；
   • F1断裂面可见红褐色片麻岩与灰黑色片麻岩的岩性分界面（110°∠37°）。

变形迹象

1. 主要变形区：
   • 两处主崩塌区（色拉1区、2区）
   • 一处河岸崩塌区
   • 四处钻孔（其中2号孔在85米深处发现疑似滑动面的破碎带）
2. 裂缝系统：
   • 共发现26条拉张裂缝，其中：
   ◦ 长度＞40米：7条
   ◦ 20-40米：3条
   ◦ ＜20米：16条
   • 最大开裂宽度50厘米，最大深度150厘米
   • 部分裂缝在坡向形成阶梯状错动，最大阶高100厘米（图2c）
3. 空间分布：
   • 裂缝呈NE30°-35°方向展布，集中分布于坡体上部
   • 未形成贯穿性裂隙，但显示多级微型滑坡平台

成因分析

结合雄松群片麻岩的矿物定向排列特征和断裂构造，认为：

1. 雄松-索瓦隆断裂的活动改变了岩体完整性；
2. 片麻岩各向异性为滑坡发育提供了优势结构面；
3. 这些地质条件共同构成了边坡失稳的内因基础（Bucci等，2016；Liu等，2021c；Qi等，2021）。

2.3 数据集

本研究使用了以下数据源：

1. SAR 图像数据：使用 C 波段 Sentinel-1 卫星的降轨 SAR 数据集，覆盖时间范围为 2014 年 10 月至 2022 年 4 月，可通过提供的网址（esa.int）获取。
2. 数字表面模型（DSM）：2023 年 4 月，利用 FEIMA-UAV（D200）无人机摄影测量生成了厘米级精度的数字表面模型。
3. 数字高程模型（DEM）：精度为 8 m。
4. 地质图：1:200,000 比例尺地质图，可通过中国数字地质图书馆（ngac.cn）获取，并结合其他地质数据进行分析。

---

3. 算法与实现

为克服当前研究的局限性，我们引入了一种混合深度学习方法——时空图卷积网络（STGCN），该方法最初用于交通网络预测。我们将滑坡中物质的运动类比为交通网络中的车辆流动，将 InSAR 数据点视为路口节点。这一类比使得 STGCN 能够有效适配于滑坡预测，并充分利用其处理动态空间关系的能力。

据我们所知，这是首次在滑坡预测中明确将物质运动作为空间属性纳入分析，这一创新在该领域具有重要突破性意义。

为了验证 STGCN 方法的优越性，我们选取了四种基准方法进行对比：

• 多层感知机（MLP）
• 循环神经网络（RNN）
• 长短时记忆网络（LSTM）
• 随机森林回归（RF Regressor）

此对比实验旨在展示 STGCN 在捕捉和预测滑坡复杂时空动态方面的增强能力。

3.1. 时空卷积块（ST-Conv Block）

如第1章所述，预测模型必须能够同时处理$空间$和$时间$信息，因此需要具备$卷积结构$和$递归结构$。为实现这一目标，我们设计了$STGCN$框架的核心——$可堆叠ST-Conv模块$，其结构如图3所示。

每个$ST-ConvBlock$由$两个时间门控卷积层$和$一个中间空间图卷积层（SGCN）$组成。这种配置使模型能够同时处理空间和时间信息。$SGCN$主要用于处理$InSAR$点云数据，以监测滑坡动态（Li, 2022; Liao et al., 2022）。

1. 空间图卷积层（SGCN）

• 节点（Nodes）：代表具有时间特征的$相干点（coherentpoints）$。
• 边（Edges）：表示$相干点$之间的$空间关系$和$物质运动方向$，主要编码$空间特征$。

$SGCN$采用$谱图卷积（SpectralConvolution）$来捕捉节点之间的$空间依赖关系$。具体计算过程在3.2节详细说明。其基本原理如下：

1. 输入数据进行$傅里叶变换（FourierTransformation）$，卷积核对节点特征赋权，以捕捉$长距离依赖关系$。
2. $邻接矩阵（AdjacencyMatrix,A）$定义了节点之间的$直接连接$，并通过$图拉普拉斯算子（GraphLaplacianOperator）$对特征进行传播。

$SGCN$的核心计算公式如下（Yu et al., 2018; Zhang et al., 2021）：
$$L=D-A$$
$$\text{GraphConv}(X,L)=\sigma (LXW)$$
$${\hat{x}}_{gconv}=\text{ReLU}({\hat{x}}_{\text{input}}+\text{GraphConv}(x,\theta ,K_s,c_i,c_o))$$
其中：

• $L$：拉普拉斯矩阵（Laplacian Matrix）
• $A$：权重邻接矩阵（Weight Adjacency Matrix），表示节点之间的连接关系
• $D$：度矩阵（Degree Matrix），对角元素表示每个节点的连接数量
• $W$：可学习的权重矩阵（Learnable Weighting Matrices）
• $\sigma$：激活函数（Activation Function）
• $\text{ReLU}$：修正线性单元（Rectified Linear Unit）
• ${\hat{x}}_{gconv}$：空间卷积的输出
• ${\hat{x}}_{\text{input}}$：空间卷积的输入
• $x$：输入的$3D$张量（3D Tensor）
• $\theta$：可训练卷积核的参数
• $K_s$：谱图卷积的阶数
• $c_i,c_o$：输入和输出通道数

该图卷积层能够利用$信息传播和聚合机制$来提取$滑坡时空特征$（Wang et al., 2023a; Wu et al., 2023）。

---

2. 时间门控卷积层（Temporal Gated Convolution）

时间门控卷积层用于从$时间序列$中提取$时间依赖信息$。本层采用$一维卷积（1DConvolution）$，卷积核宽度$K_t$可根据数据需求调整。

• 该卷积层输出两个值：
  • $线性变换输出$
  • $门控输出（GatingOutput）$

这两个输出由$门控线性单元（GatedLinearUnit,GLU）$ 处理，其公式如下：
$$Y=P\odot \sigma (Q)$$
其中：

• $Y$：时间门控卷积的输出
• $P,Q$：一维卷积产生的矩阵
• $\sigma$：Sigmoid激活函数
• $\odot$：Hadamard逐元素乘积（Element-wise Hadamard Product）

$GLU$允许模型$动态调整保留或丢弃的信息$，提高预测的$时序适应能力$，从而$增强模型对时间序列数据的处理能力$。

---

3. ST-Conv Block 计算流程

$ST-ConvBlock$结合了$时间门控卷积$和$空间图卷积$，其计算公式如下：
$$v^{(l+1)}={\theta }^{(l1)}\cdot \text{GatedConv}\left(\text{GraphConv}({\theta }^{(l0)}\cdot v^l,L)\right)$$
其中：

• $v^l$：第$l$层的输出
• $v^{(l+1)}$：第$l+1$层的输出
• ${\theta }^{(l0)},{\theta }^{(l1)}$：神经网络可训练权重矩阵

此结构使$ST-ConvBlock$能够有效捕捉和利用$滑坡的时空动态特征$，从而提升$预测准确性$。

3.2 基于InSAR的STGCN时空预测的实现

整个实现过程可分为三个部分：InSAR反演滑坡位移时间序列、数据预处理以及STGCN预测滑坡变形。具体步骤请参考图4。

---

第一部分：InSAR滑坡位移时间序列反演

滑坡位移时间序列反演基于GAMMA SAR干涉测量软件（由瑞士GAMMA Remote Sensing AG公司开发），采用SBAS-InSAR方法。

使用Sentinel-1 A高精度轨道数据来校正轨道误差。然而，随着主影像与子影像的时间间隔增加，校正精度逐渐降低，甚至无法满足后续处理需求。此外，由于2017年3月卫星轨道调整，导致调整前后校正精度发生突变。为了解决这一问题，采用了双向配准策略：

1. 首先，对轨道调整前后的两幅影像进行配准。
2. 然后，利用这两幅影像分别作为主影像，对调整前后的数据集进行二次配准。

尽管双向配准会降低部分干涉图对的精度，但能够提升整个数据集的整体校正精度。

为了确保干涉图质量并减少计算量，需要为SAR影像设置基线阈值。对于Sentinel数据，选择了时间基线120天，空间基线120米，最终生成403幅干涉图。

干涉处理流程包括干涉图生成、自适应滤波和相位解缠**。随后，通过解缠相位与DEM数据进行精密基线估计，并迭代计算干涉处理。为了连接子集，采用奇异值分解方法（SVD）。同时，考虑到大气相位在时间域上低相干、在空间域上高相干的特性，对数据进行大气滤波。最终，完成滑坡位移时间序列的获取。

---

第二部分：用于STGCN变形预测的数据预处理

数据预处理可分为三个步骤：

1. 时间序列步长统一化
2. 数据加载及自相关分析
3. 时空权重计算

步骤 1：时间序列插值

STGCN模型需要等间隔采样的时间序列，因此对于缺失数据点需要进行插值。由于滑坡具有非线性特征，为了更精准地捕捉滑坡的复杂动力学特性，评估了多种插值方法，包括：

• 高斯过程回归（GPR）
• 样条插值（Spline Interpolation）
• 多项式插值（Polynomial Interpolation）
• 径向基函数插值（RBF Interpolation）

为了验证插值效果，随机选择10个点作为验证数据集，其余数据用于插值计算。影子点分析（Shadow Point Analysis） 用于比较插值值与真实值的接近程度。此外，还使用核密度分析（Kernel Density Estimation） 和 相关性分析（Correlation Analysis） 进行验证。

**实验结果（见附录图S1）**表明：

• 高斯过程回归（GPR）和RBF插值的效果最优。
• 其中，GPR插值能够提供残差（sigma）值，便于误差分析，因此选择GPR作为最终插值方法。

核密度估计及相关性分析也进一步验证了GPR插值的可靠性（参见图S1c-e）。插值残差最大值为0.6 mm，相比滑坡位移的数量级（分米级）可以忽略不计。但需要注意，在滑坡前缘（崩塌区）处，sigma值略高，表明非线性变形较为明显。

---

步骤 2：数据加载及自相关分析

数据加载模块将原始InSAR数据转换为STGCN输入格式的三维张量，其形状为：
$$[N,T,S]$$
其中：

• $N$：空间节点数
• $T$：时间维度
• $S$：标准化序列单元

首先，提取原始InSAR时间序列数据，并填充缺失帧，最终得到229个有效帧。去除初始全零帧后，保留228个帧用于分析，此时数据结构为：
$$[N,T]$$

在标准序列单元生成过程中，采用滑动窗口方法对时间序列进行分割，每个子序列形状为：
$$[N,S,C]$$
其中：

• $C$：输入通道数

为了优化预测窗口，分析了Sela滑坡的平均位移时间序列，并计算其自相关函数（ACF）。结果表明：

• 随着时间跨度的增加，自相关性逐渐降低
• 当时间跨度达到228天，自相关性低于置信区间（蓝色阴影区域），意味着当前滑坡状态与228天前的状态没有显著相关性（如图5a）。
  

因此，我们选取19个时间帧作为序列长度，其中：

• 10个帧作为历史输入
• 9个帧作为预测输出（如图5b）。

数据集按照**$T-S+1$个窗口进行分割，模型通过前10步预测后9步**进行训练（如图5b）。

最终，本研究使用前120天历史数据预测未来108天的滑坡位移。然而，对于更长期的预测（超过108天），会超出模型预测范围。

数据归一化后，划分为训练集、验证集和测试集：

• 训练集：前207帧，用于训练模型并学习滑坡的时空动态特征
• 测试集：最后21帧，用于评估模型预测能力
• 验证集：训练集中的19帧，用于超参数调整（如图5b）

最后，利用**批处理函数（Batch Function）**将数据整理为批量形式：
$$[B,N,S,C]$$
其中：

• $B$：批大小

这些批量数据被直接输入STGCN模型进行训练和预测。

步骤 3：时空权重计算

在滑坡过程中，节点之间的交互包括时间关系（WT）和空间关系（WS）（Fang et al., 2024; Liu et al., 2019; Xi et al., 2023）。滑坡作为非线性系统，受复杂环境因素影响，使得这些关系的数学表达式变得异常复杂。因此，对这些关系的量化计算一直是一项具有挑战性的工作。

在本研究中，我们选择了一种基础方法来解决这一问题：

• 将Sela滑坡的物质运移方向视为主要的空间关系。
• 空间权重$WS$ 计算方式为：两个相干点构成的空间向量与主要滑动方向的点积。
• 时间权重$WT$ 采用皮尔逊相关系数进行计算。

由于Sela滑坡的坡向为$127^{\circ }$，几乎垂直于卫星视线方向$38.9^{\circ }$，因此我们未引入额外轨道的SAR数据，而是直接简化滑坡物质运移方向为坡向。

空间权重计算

空间权重$WS$的计算公式如下：
$$WS=\overrightarrow{PiPj}\cdot \overrightarrow{a}(6)$$
其中：

• $\overrightarrow{a}$：主要滑动方向向量
• $\overrightarrow{PiPj}$：两个相干点之间的空间向量

时间权重计算

时间权重$WT$采用皮尔逊相关系数计算：
$$WT=\rho (X,Y)=\frac{\text{cov}(X,Y)}{{\sigma }_X{\sigma }_Y}(7)$$
其中：

• $\rho (X,Y)$：变量$X$与$Y$之间的皮尔逊相关系数
• $\text{cov}(X,Y)$：$X$与$Y$的协方差
• ${\sigma }_X$、${\sigma }_Y$：$X$和$Y$的标准差

联合时空权重计算

空间权重$WS$和时间权重$WT$通过**参数$\alpha$**进行统一，得到最终的权重$W_{ij}$：
$$W_{ij}=\alpha WS+(1-\alpha )WT,WS<W{S}_0,WT>W{T}_0(8)$$
其中：

• $W{S}_0$：空间权重阈值（本研究设定$W{S}_0=300$ m）
• $W{T}_0$：时间权重阈值（本研究设定$W{T}_0=0.1$）

为了简化计算并限制权重的可控范围，我们引入了空间和时间阈值：

• 当时间相干性低于 $0.1$ 或空间距离大于 $300$ m 时，权重设为 0。

最终的加权邻接矩阵的热图（子采样结果）见数据预处理部分（图4）。

---

第三部分：Sela滑坡位移的时空预测

为了后续对比实验的公平性，本研究未使用堆叠模型，而是采用单个ST-Conv Block进行训练。

计算平台及软件的详细信息见表S1和S2，STGCN模型的具体参数见表1。

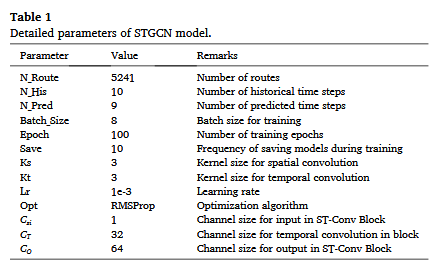
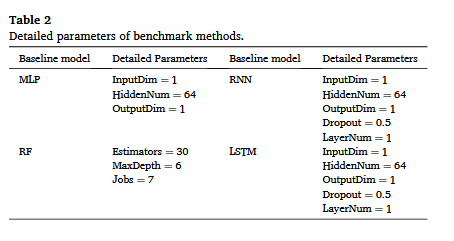
防止过拟合的策略

1. 指数衰减学习率
训练过程中，学习率每5步衰减0.7倍（见图6），以确保模型在早期快速收敛，同时避免后期过拟合或过冲。

2. 适应性优化器
使用RMSProp或ADAM优化器，自适应调整各参数的学习率，以加速收敛。

3. Dropout正则化
训练时，每个神经元的保留概率为0.5，即每次迭代随机丢弃50%的神经元，以减少过拟合，提高泛化能力。

4. L2正则化损失
模型性能评价采用L2损失函数：
$$\mathcal{L}=\sum _{i=1}^N||{\hat{y}}_i-y_i|{|}^2(9)$$
其中：

• ${\hat{y}}_i$：模型预测值
• $y_i$：真实值

每50步记录一次训练损失，并在每个epoch结束时对指定时间步长进行预测，并计算预测误差（MAPE、MAE、RMSE）。

该方法能够提高推理效率，并帮助模型捕捉滑坡位移的时间依赖性。但该方法需要更高的计算资源，并且无法对每个时间步长的误差进行逐步调整。

批量大小与训练轮数的选择

批量大小和训练轮数的选择依据数据集规模和模型复杂性（见表1）。为了增强泛化能力并最小化过拟合，本研究采用动态批量处理、数据随机化、学习率衰减和L2正则化（Bengio, 2012; Smith, 2017）。

TensorBoard 用于记录训练损失、拷贝损失和学习率，提供模型训练过程中不同轮数的可视化表现（见图6）。

损失函数

模型的训练损失（见图6）由以下公式定义：
$$\hat{L}(v;W_{\theta })=\sum _t\Vert {\hat{v}}_t-v_t{\Vert }_2^2$$
其中，

• $W_{\theta }$：包含模型中的所有可学习参数
• $v_t$：真实值
• ${\hat{v}}_t$：预测值

在每个训练轮次（epoch） 结束后，模型将在验证集上进行评估。如果性能提升，则更新模型。

---

STGCN 模型结构

模型采用多步迭代预测，即：

1. 上一时间步的预测结果作为下一时间步的输入，逐步生成序列预测结果。
2. 历史观测数据 通过输入层进入时空卷积模块，进行时空特征提取。

数据首先通过时间卷积层提取时间特征：

• 输入形状：$[B,N,S,C_{in}]$
• 经过时间卷积后，输出形状：$[B,T-K_t,S,C_{out}]$
• 其中，$K_t$ 为时间卷积核大小

随后，图卷积层（Graph Convolution） 提取节点间的依赖关系：

• 输入形状：$[B,N,C_{in}]$
• 结合邻接矩阵和可学习卷积核参数，节点间信息传播后，输出形状：$[B,N,C_{out}]$

之后，输出数据再经过第二层时间卷积层 以提取额外的时间特征：

• 卷积后形状：$[B,T-2K_t+2,C_{out}]$

正则化与Dropout

• 层归一化（Layer Normalization）：稳定训练过程
• Dropout层（随机丢弃神经元）：减少过拟合风险

最后，数据通过输出层：

1. 经过时间卷积层，将多步预测转换为单步预测，输出形状变为 $[B,1,N,C]$
2. 通过全连接层，映射到单通道数据，最终输出形状为 $[B,1,N,1]$，即每个节点的单步预测值

基准对比方法

采用四种基准模型（MLP、RNN、RF、LSTM）与STGCN模型进行对比（表2）。

• MLP（多层感知机）：包括输入层、隐藏层和输出层，主要用于捕捉非线性关系。
• RNN（循环神经网络）：用于处理时间序列数据，采用64个神经元的隐藏层和tanh激活函数，隐藏状态初始化为0。
• LSTM（长短时记忆网络）：擅长捕捉长期依赖性，包含LSTM单元、Dropout和全连接层。
• RF（随机森林回归）：采用30棵决策树，最大深度为6，并使用7个CPU核心进行并行计算。

这些方法涵盖了传统机器学习（RF）和神经网络方法（MLP、RNN、LSTM）的不同特点。

• MLP & LSTM：擅长捕捉时间序列数据中的复杂模式（Deng et al., 2023; Tiwari and Shirzaei, 2024; Wang et al., 2023b）。
• RF回归：适用于处理非线性问题，并具备良好的可解释性（Al-Najjar et al., 2023; Shu et al., 2023）。
• RNN：特别适用于时间依赖性问题。

所有方法均先在单采样点上进行测试，随后推广到整个时间序列数据以进行全面对比。

---

模型预测性能评估指标

为了严格评估模型的时空预测能力，采用五种定量指标（Yao et al., 2023; Zhang et al., 2023）：

1. 均方误差（MSE）：
   $$MSE=\frac{1}{m}\sum _{i=1}^m({\hat{y}}_i-y_i{)}^2$$
2. 平均绝对误差（MAE）：
   $$MAE=\frac{1}{m}\sum _{i=1}^m|{\hat{y}}_i-y_i|$$
3. 平均绝对百分比误差（MAPE）：
   $$MAPE=\frac{1}{m}\sum _{i=1}^m\left|\frac{{\hat{y}}_i-y_i}{y_i}\right|\times 100$$
4. 解释方差（Explained Variance，EVar）：
   $$EVar=1-\frac{{\sum }_{i=1}^m({\hat{y}}_i-y_i-(\hat{y}-y){)}^2}{{\sum }_{i=1}^m(y_i-y{)}^2}$$
5. 结构相似性指数（SSIM）：
   $$l(x,y)=\frac{2{\mu }_x{\mu }_y+(k_{1}L{)}^2}{{\mu }_x^2+{\mu }_y^2+(k_{1}L{)}^2}$$
   $$c(x,y)=\frac{2{\sigma }_x{\sigma }_y+(k_{2}L{)}^2}{{\sigma }_x^2+{\sigma }_y^2+(k_{2}L{)}^2}$$
   $$s(x,y)=\frac{{\sigma }_{xy}+(k_{2}L{)}^2/2}{{\sigma }_x{\sigma }_y+(k_{2}L{)}^2/2}$$
   其中：

• ${\mu }_x,{\mu }_y$：图像$x,y$的均值
• ${\sigma }_x,{\sigma }_y$：图像$x,y$的标准差
• ${\sigma }_{xy}$：图像$x$与$y$的协方差
• $k_1,k_2$：常数参数
• $L$：像素动态范围

4. 结果与分析

4.1. Sela 斜坡的变形区域及过程特征

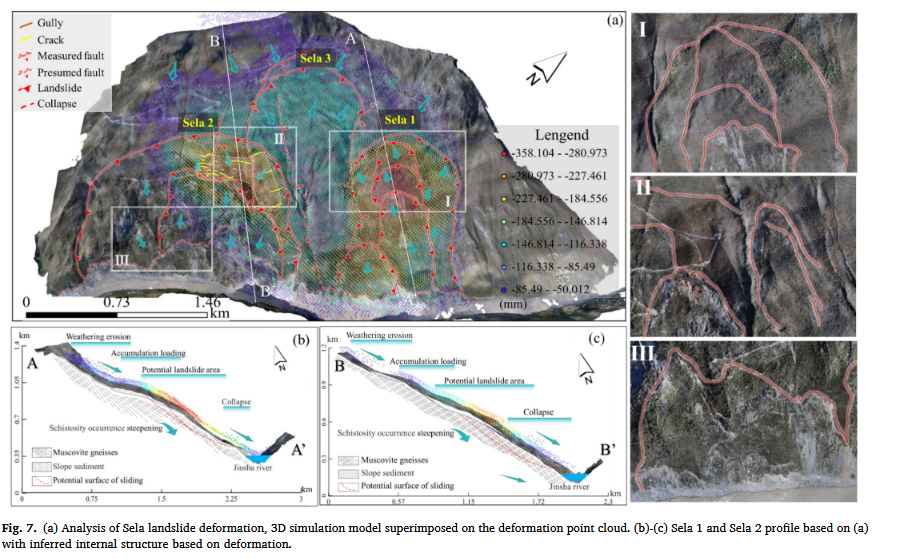
利用 SBAS-InSAR 技术，我们获取了 2014 年 10 月 12 日至 2022 年 4 月 9 日 期间 Sela 斜坡的 累积位移数据。为了提高空间精度，我们结合了 无人机摄影测量（UAV）生成的 3D 模型 与 InSAR 获取的变形点云数据，构建了 混合变形模型。

如 图 7 所示，InSAR 结果 与 无人机影像识别的变形区域高度吻合。通过 交叉验证，我们重新定义了 滑坡边界（见图 2），并将 Sela 滑坡划分为 三个区域：

1. Sela 1 区域

   • 沟谷 G1 作为 右侧边界。
   • 该区域包含 三个次级滑动区，每个区域均被 陡坡 包围。
   • 中心区域变形最为剧烈，其中 中央滑动带呈现明显的崩塌特征（见图 7I）。

2. Sela 2 区域

   • 沟谷 G2 作为 左侧滑动边界。
   • 拉张裂缝 作为 后缘边界（见图 7II）。
   • 坡脚处发生多次崩塌，导致 SBAS-InSAR 数据出现局部不一致（见图 7III）。

3. Sela 3 区域（中间过渡带）

   • 该区域因 断层作用 形成了一条 物质运移通道，使得滑坡物质流入 金沙江，形成 明显的泥石流地貌（G2）。
   • 该通道的存在 阻碍了斜坡中部沉积平台的形成。

为了进一步分析 Sela 斜坡的变形特征，我们提取了 两个剖面结构图（图 7），并将变形过程归类为 三种类型：

1. 风化侵蚀（坡顶）

   • 坡顶裸露的白云母片麻岩 长期暴露于空气中，发生 持续风化剥蚀。
   • 破碎岩体在重力和降水作用下逐步向下迁移。

2. 缓慢蠕滑（坡中）

   • 由于物质不断堆积，坡中形成 沉积平台。
   • 随着 时间推移，沉积物不断累积，增加坡体载荷，进一步 增强向下滑动力（Bucher et al., 2015; de Obeso & Kelemen, 2020）。

3. 剧烈崩塌（坡脚）

   • 坡中沉积物的持续堆积 导致斜坡负荷增加，使得坡脚发生剧烈滑动和崩塌。

---

4.2. Sela 表面位移时间序列分析

时间序列分析 对于理解滑坡演化机制及 预测未来变形趋势 具有重要意义。图 8 展示了 2014 年 10 月至 2022 年 4 月 Sela 斜坡表面的 演化过程。

• 图 8 每个帧（frame）均独立编号，左侧标注了 起始与结束时间 及 时间跨度（单位：天）。
• 采用 HLS（色调-亮度-饱和度）颜色渲染 以增强视觉效果。
• SAR（合成孔径雷达）影像 作为 时间序列的底图。
  

图 8 的关键发现：

• Sela 斜坡的变形在 2014 年之前已经开始，表明该区域具有 长期不稳定性。

• 2016 年（帧 2）和 2018 年（帧 5）出现明显的变形加速信号。

  • 2018 年的信号 与 白格滑坡（Baige landslide） 事件相关（Chen et al., 2021; Gao et al., 2021; Hu et al., 2020）。
  • 2016 年的信号 没有对应的已记录事件。
  • 我们推测 2016 年的变形加速 可能与 金沙江水位急剧上升 相关（Liu et al., 2021c）。
  • 降水数据排除了暴雨诱发的可能性，但 上游洪水仍可能是诱因。
  • 具体成因尚不确定，可能与 异常气候条件 相关（Lei et al., 2019; Santoso et al., 2017）。

• 图 8 的帧 7 和帧 8 显示，Sela 斜坡仍处于持续变形阶段，尚未出现明确的 加速变形拐点。

---

4.3. STGCN 模型与基准方法的性能评估

表 3 总结了 三种时间帧（每 36 天一幅影像：2022-01-27 / 2022-03-04 / 2022-04-09） 下，各模型在 五种评估指标 上的表现。结果表明，STGCN（时空图卷积网络）始终优于基准模型，在 均方误差（MSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE） 方面均取得显著提升。

在 四种基准模型 中：

• 多层感知机（MLP） 性能最佳；
• 随机森林（RF） 次之；
• 长短时记忆网络（LSTM） 表现最差；
• 循环神经网络（RNN） 仅优于 LSTM，但劣于 MLP 和 RF。

这一结果可能与数据集 时间密度有限 相关，使得 MLP 和 RF 在时间信息利用上表现更优，而 LSTM 受限于时序信息不足，导致预测效果较差。

---

误差分布分析

图 9 和图 14 分别采用 箱线图和三维散点图 对误差分布进行了分析：

• 图 9 显示了 绝对误差（AE）和绝对百分比误差（APE），STGCN 在捕捉高值区域时表现突出，同时保持较低的平均误差。
• STGCN 的整体平均误差 略优于其他基准方法，但在 异常值（高值区域） 方面，STGCN 略逊于 MLP，但优于 RF。
• MLP 和 RF 在平均误差指标上相近。
• 相对误差分析 显示，STGCN 在整体平均误差和高值区域误差捕捉上均优于其他方法。
• LSTM 在绝对误差和相对误差上均表现不佳，说明其在建模数据动态变化方面存在局限性。
• RNN 虽优于 LSTM，但仍落后于 MLP 和 RF，表明其在捕捉时序依赖关系方面仍不如其他模型稳定。

---

STGCN 预测精度随时间下降的可能原因

像许多预测模型一样，STGCN 的精度会随时间推移而下降，可能受以下因素影响：

1. 滑坡演化的非平稳性：
   • 滑坡受 气候变化、人类活动、地质过程 等多种环境因素影响，这些因素 随时间变化，可能无法完全在训练数据中体现，导致模型在长期预测时精度下降。
2. 预测误差的累积：
   • 即使是 初始预测误差较小，长期预测时 小误差可能会逐步积累，最终导致 较大偏差。
3. 模型过拟合：
   • 如果 STGCN 对训练数据过拟合，在面对 新数据或未见过的条件 时，可能 适应能力较弱，导致长期预测表现下降。

---

空间误差分布特征

图 10 展示了误差的空间分布（每 36 天一幅影像），揭示了研究区域内的 重要误差模式：

• STGCN 误差具有明显的空间聚集特征，主要集中在 核心区和坡脚，说明模型对这些地形特征较为敏感。
• 核心区的误差聚集与 Sela 1 区域的剧烈滑坡现象一致（见图 7I），与 无人机摄影测量 和 实地调查 结果相符。
• STGCN 模型的核心区误差比其他模型更明显，可能是因为 STGCN 能够捕捉空间特征，并通过 信息传播与聚合 反映空间依赖性。然而，这种机制可能 在局部非线性变形较强的区域，限制模型对空间特征的捕捉能力，导致误差累积。

不同模型的误差特征：

• RF（随机森林）：
  • 误差主要集中在 表面变形较明显的区域，而在 变形较小的区域 误差相对较小。
  • RF 在处理 复杂非线性关系 方面表现出色，但 难以捕捉局部精细特征，导致误差呈 簇状分布。
• MLP、RNN、LSTM 误差分布较为分散：
  • MLP 误差整体较低，远优于 LSTM。
  • RNN 能够捕捉时序依赖性，但在 建模复杂特征方面仍有不足。
  • LSTM 在长期时间依赖性和非线性建模上表现良好，但 误差较大且分布较分散，表明其在本应用场景下 效果较差。
  • LSTM 训练时间较长，超参数调优复杂，进一步影响其应用。

---

误差分布模式分类

• 簇状分布（Clustered Distribution）：
  • 例如 STGCN 和 RF，误差集中于特定区域，有助于 识别和修正问题区域，解释性强。
  • 但 簇状误差也可能表明局部性能较差，受极端现象影响较大。
• 随机分布（Random Distribution）：
  • 例如 MLP、RNN 和 LSTM，误差较均匀，表明 模型整体性能较稳定，受局部异常影响较小。
  • 但这种分布 难以精准定位误差源，解释性较弱。
    
    

---

4.4. Sela坡面位移的时空预测

在完成对 原始数据集 的训练后，STGCN 模型被用于 预测塞拉坡面的地表变形数据。本次预测涵盖了 2022 年 4 月 9 日至 2023 年 10 月 1 日 期间的 45 帧数据，该时间范围超出了原始数据集的范围。

---

预测数据可视化与验证

• 为了构建 3D 表面地图，从这 45 帧预测数据 中 平均每 108 天选取 6 帧 进行可视化，如 图 11 所示。
• 预测的变形空间分布（图 11）与训练集观察结果（图 7）高度一致，说明模型的预测趋势与真实变形趋势相符。
• 变形区域的边界逐渐扩展，但 变形值的变化幅度并不显著，这可能与滑坡区域的地质条件有关。
  

---

代表性点的时序分析

为了验证模型的预测能力，在变形区域内均匀选取了 5 个代表性点，并进行了时间序列分析：

1. 首先根据变形幅度大小，将所有点划分为 5 个类别（从大到小）。
2. 然后在每个类别中随机选取一个点，共得到 5 个代表性点。
3. 图 12 展示了 5 个代表性点的数值变化曲线，用于评估模型的预测表现。
   

---

预测趋势分析

• 在最后 9 帧数据（预测区间后半段）中，模型预测曲线整体与真实观测数据保持一致，表明模型能够准确预测滑坡的长期趋势。
• 唯一的例外是 P4 点，该点位于剧烈塌陷区域，该区域可能存在 高度非线性或突发变形，导致模型难以精准预测。
• 模型预测结果在 9 帧后趋于收敛，这通常表明：
  • 模型已接近预测阈值，即短期预测能力较强，但长时间预测能力可能受限。
  • 预测能力达到饱和状态，可能需要引入更多外部因素（如降雨、地震等环境因素）来提升长期预测的准确性。

---

5.1 塞拉滑坡的驱动因素、变形特征及破坏模式分析

(1) 构造作用与地质背景

• 板块碰撞与地壳抬升：印度板块与欧亚板块的俯冲碰撞持续推动青藏高原的隆升。这一过程中，古特提斯洋逐渐消失，留下了多个构造缝合带（Jiang et al., 2021）。
• 缝合带内应力集中：由于板块运动，剪应力在缝合带内高度集中，导致断裂与褶皱发育（Zhao et al., 2023）。本研究区位于JRSZ 构造缝合带内，具有强烈的构造活动背景。
• 主要岩性：现场调查表明，塞拉坡体主要由前寒武纪雄松组（Xiongsong Formation）云母片麻岩组成，岩石片理性显著，矿物定向排列（图 1c）。

---

(2) 构造演化对坡体稳定性的影响

• 长期的地壳隆升、构造运动及河流下切（Schumm, 1986）持续改造塞拉坡体。
• 多阶段构造活动 重塑了坡体岩块结构，使不同成因、不同时代的构造面（如断裂、卸荷裂隙）交错分布，形成破碎的岩体结构（见图 2）。
• 金沙江的侵蚀作用 进一步塑造了河谷两侧的陡峭斜坡，使坡体处于重力卸荷作用 下，易引发滑坡和崩塌（Wang et al., 2021b）。
• 无人机影像（图 7III） 证实，坡体前缘的土石持续崩解和滑动，进一步加剧了坡体的暴露，使其处于持续蠕变变形状态（Yao et al., 2022）。

---

(3) 变形模式与滑坡类型

• 坡体中部：张裂与台阶状地貌——蠕变变形表现为张裂缝和阶梯状地貌，无人机影像（图 2、图 7）清晰显示出裂隙发育区域。
• 滑坡类型：牵引式滑坡（Traction-type landslide）——滑坡后部持续失稳，导致前缘变形加剧，最终呈现蠕滑-牵引裂解型滑坡模式。
• InSAR 监测（图 8） 表明，过去 9 年间，塞拉坡体一直处于持续的蠕滑变形状态，并在2018 年发生两次显著加速事件。
• 加速信号的成因：
  1. 2018 年白格滑坡引发的洪水（Chen et al., 2021）。
  2. 金沙江水位的不明原因急剧上升（Liu et al., 2021b），可能与极端气候事件有关。

---

(4) 水文因素对坡体稳定性的影响

• 洪水事件的影响（图 12）：
  • （a）土壤饱和度上升：河流水位的急剧上升导致土壤饱和度增加，提高孔隙水压力，降低剪切强度，加剧变形（Handwerger et al., 2019）。
  • （b）水下侵蚀作用：河水冲刷坡脚，削弱基岩支撑，导致坡体稳定性降低（Lacroix et al., 2020；Shi et al., 2015）。
  • （c）坡脚剪切强度降低：水位上升导致坡脚被侵蚀削弱，降低安全系数（FS），增加坡体失稳的可能性（Cao et al., 2021；Cheng et al., 2022）。

---

5.2 STGCN 融合时空动态特征以提升滑坡预测能力

基于前述分析，塞拉滑坡由两个不同的变形区域（Sela 1 和 Sela 2） 组成，它们表现出不同的变形特征和模式，包括崩塌、蠕滑和张裂。传统方法通过选取特征点进行分析，但这种方式难以全面捕捉塞拉滑坡的整体空间变形特征。

STGCN 模型通过整合时空动态信息，并结合物质迁移机制（详见 5.3 节），实现了更优的预测效果：

• 相较于其他模型，STGCN 具有更高的平均预测精度和更聚集的误差分布，主要得益于其架构设计。
• 其基础架构包括：
  • 两个时间层（Temporal Layers）：采用门控循环单元（GRU） 处理时间序列信息。
  • 一个空间层（Spatial Layer）：使用图神经网络（GNN） 解析空间拓扑关系。

---

(1) GNN 结构的优势

• GNN 可有效建模复杂节点间的相互作用，通过精确调整权重 提取关键特征（Cheng et al., 2022；Hu et al., 2022；Liu et al., 2022c）。
• 与传统方法不同：
  • 以往研究主要关注相邻空间节点间的局部关系，忽略了整体网络的连通性和全局结构。
  • 许多研究采用规则网格划分或分段方法，导致网络结构割裂、丢失空间信息。
  • 本研究直接在图结构数据上执行卷积运算（Graph Convolution），提取更具意义的空间模式（见图 13）。
• 计算优化策略：
  • 切比雪夫多项式近似（Chebyshev Polynomials Approximation）。
  • 一阶近似（1st-order Approximation）。
  • 通过上述方法降低计算开销，使 GNN 在大规模数据上高效运行（Yu et al., 2018；Zhang et al., 2021）。
    

---

(2) GRU 的时间序列建模能力

• GRU 能够高效处理时间序列数据，捕捉滑坡演化过程中的动态变化（Phuong Thao Phuong Thao Thi et al., 2021；Wang et al., 2020）。
• 结合 GNN 与 GRU，STGCN 不仅能提取单点的位移信息，还能全面捕捉节点间的空间联系，提升预测准确性（Luo et al., 2021；Wang et al., 2023a；Wu et al., 2023）。
• 特别适用于 InSAR 监测数据的滑坡预测，可解析复杂空间关系（见图 10）。

---

5.3 时空关系对滑坡预测的影响分析

为进一步评估 STGCN 模型的性能，我们进行了一系列对比实验，测试不同权重配置对预测效果的影响：

1. WST（同时考虑时空关系）。
2. WT（仅考虑时间关系）。
3. WS（仅考虑空间关系）。
4. W0（不考虑时空关系，相当于在规则栅格数据上进行卷积计算）。
   
   实验结果（见图 13 和 14）表明：

• 当同时考虑时空关系（WST）时，模型表现最佳，预测误差显著降低。
• 控制组 W0 表现最差，表明忽略时空关系会大幅降低预测精度。
• 高值异常区域（图 7I）在四个实验组中空间分布基本一致，表明该区域的误差主要源于非线性变形特征，而非时空异质性。
• WST 组不仅在误差高值区的覆盖范围上表现更优，其绝对误差值也显著低于其他组，进一步证实 STGCN 在捕捉滑坡时空特征方面的优势。

5.4 ST-Conv Block 数量对 STGCN 预测性能的影响分析

为探讨 STGCN 模型中ST-Conv Block 的数量对预测性能的影响，我们设计了一系列对比实验，评估了以下三种配置：

1. 单个 ST-Conv Block。
2. 两个 ST-Conv Blocks。
3. 三个 ST-Conv Blocks。

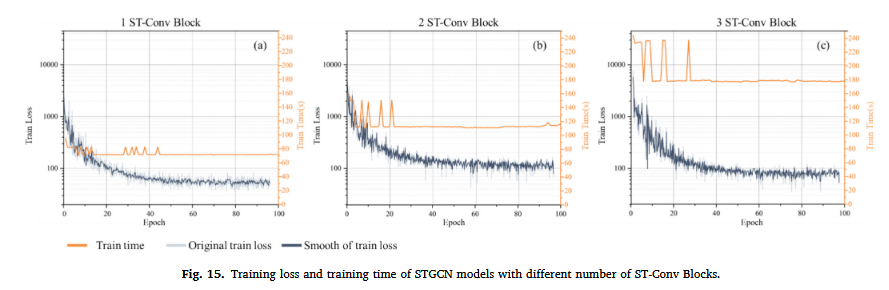
实验结果见图 15 和表 5，同时，我们在附录中提供了三种配置的误差分布与箱线图，供有兴趣的研究人员进一步优化模型性能参考。

---

(1) 训练损失与训练时间

• 单 ST-Conv Block 配置（图 15a）：训练损失稳定下降。
• 双 ST-Conv Blocks 配置（图 15b）：初始训练损失下降速度更快，但最终训练损失略高于单 Block 配置。
• 三 ST-Conv Blocks 配置（图 15c）：初期损失下降迅速，但波动较大，最终训练损失略高于单 Block 配置。

结果表明：增加 ST-Conv Block 的数量会线性增加训练时间，但可能导致更高的训练损失。

---

(2) 预测误差评估（表 5）

• 在三个测试日期（2022-01-27、2022-03-04 和 2022-04-09）的评估指标中，单 ST-Conv Block 方案的 MSE 和 MAE 值最低，表明其在捕捉整体趋势方面表现最优。
• 三 ST-Conv Blocks 方案的各项指标下降，说明过度增加复杂性会带来边际效益递减，甚至导致过拟合。
• 双 ST-Conv Blocks 方案表现居中，表明适量增加 ST-Conv Block 有助于提升预测能力，但过多会影响性能。
  

---

(3) 关键结论

• 增加 ST-Conv Block 数量并不一定提升模型性能，过多的 Block 可能降低泛化能力，甚至导致过拟合。
• 最佳选择是单 ST-Conv Block 或双 ST-Conv Blocks 配置，以在计算效率和预测精度之间取得平衡。

---

5.5 影响因素与模型的不确定性分析

尽管 STGCN 在捕捉滑坡的复杂时空关系和非线性动态特征方面表现出色，但其适用性仍受到多个因素的影响，包括：

• 地理区域、地形条件、土壤非均质性、滑坡类型、数据可用性和模型参数选择。

以下是主要影响因素及其导致的不确定性分析：

---

(1) STGCN 模型的局限性

• STGCN 主要基于数据驱动方法，专注于学习空间关系和物质迁移特征，但未直接纳入关键环境因素。
• 例如，植被覆盖、降雨模式和气候条件对滑坡动力学有重要影响，但当前模型未完全集成这些变量。
• 已有研究表明（Barik et al., 2017；Tian and Zhang, 2022），引入环境变量（如降雨量或植被指数）可提高滑坡预测精度，尤其是在气候多变的地区。

---

(2) 地形与土壤异质性

• 土壤结构的复杂性 可能导致 STGCN 难以捕捉非线性变形行为。
• 例如，在青藏高原或喜马拉雅地区，土壤和坡体结构变化显著，滑坡的变形模式更复杂，需要对模型进行针对性调整。
• 针对不同滑坡类型（如岩崩、泥石流）（Chen et al., 2024；Zhang et al., 2022b），可考虑：
  • 增加卷积层深度，增强特征提取能力。
  • 融合额外的环境变量（如水文数据），提升模型适应性。

---

(3) 预测不确定性来源

通过对模型敏感性分析，我们发现 STGCN 预测的不确定性主要来自以下三方面：

1. 模型不确定性

   • 主要源于模型结构的局限性 或 训练过程中的随机性。
   • 例如，我们使用 Dropout 正则化 防止过拟合，但这也会引入额外的不确定性，导致不同网络训练出的预测结果略有波动。
   • 研究表明（Tian and Zhang, 2022），正则化技术在提升泛化能力的同时，也可能因训练过程的随机性导致预测结果波动。

2. 数据不确定性

   • 特别是在 InSAR 数据处理过程中，数据误差对预测结果的影响尤为关键。
   • 尽管 InSAR 具有毫米级到亚毫米级精度，但时间序列归一化等处理步骤可能引入进一步的不确定性。
   • 为降低误差，我们使用 高斯过程插值（Gaussian Process Interpolation），可将插值误差控制在1 mm 内（见图 S1b）。
   • 但即便如此，在高敏感区域，输入数据的细微误差仍可能显著影响模型预测（Liu et al., 2022b）。

3. 参数不确定性

   • 模型性能对学习率、批量大小（batch size）和网络结构等超参数较为敏感（见附录图 S3 和 S4）。
   • 参数调整对于获得最佳预测效果至关重要（Liu et al., 2022a；Liu et al., 2024）。

---

5.6 适应性与局限性分析

(1) 不同类型滑坡的适应性挑战

STGCN 模型在适应不同类型滑坡时面临的主要挑战在于滑坡的演化过程差异。不同类型的滑坡在触发机制和空间尺度上存在显著不同：

• 浅层滑坡（Shallow Landslides）：通常由强降雨作用于松散表层物质而触发，滑坡动力学相对简单。
• 深层滑坡（Deep-Seated Landslides）：涉及深部地质结构，其动力学更复杂，受到地质构造、应力变化等因素的影响（Sidle and Bogaard, 2016）。

因此，预测不同类型的滑坡需要针对其物理特性和行为特征，采用特定的训练数据集进行模型训练。

适应性调整建议：

1. 针对不同滑坡类型优化 STGCN 结构，例如调整卷积层深度以提取更深层次的特征。
2. 使用多样化的数据集进行训练，确保模型能有效捕捉不同滑坡类型的独特特征。

---

(2) 数据可用性与计算成本

• 高质量数据集的可获得性：

  • STGCN 在不同类型滑坡间泛化的关键瓶颈在于数据可用性。
  • 需要涵盖多种滑坡条件的高质量数据集，但实际中，由于地形、降雨、地质条件的不同，高质量数据往往较难获取。
  • 例如，某些地区缺乏长时间序列的 InSAR 观测数据，导致模型在此类区域的适应性下降。

• 计算复杂度的提升：

  • 引入更多数据点会增加计算需求，可能需要更复杂的训练方法以防止过拟合。
  • 计算资源需求较高，特别是在大规模滑坡预测与实时监测任务中，STGCN 可能面临计算资源瓶颈。

---

(3) InSAR 数据质量与监测频率的影响

• InSAR 数据的分辨率与覆盖范围

  • 不同地区的 InSAR 数据质量存在差异，在数据稀疏或分辨率较低的区域，模型性能可能下降。
  • 在大规模滑坡预测和实时监测任务中，数据精度和完整性尤为重要。

• 实时监测的挑战

  • 数据采集频率对于实时监测至关重要，但目前卫星 SAR 数据的更新频率可能无法满足高频监测需求。
  • 替代方案：
    • 采用地基 InSAR（Ground-Based InSAR, GB-InSAR）系统替代卫星 SAR，以满足滑坡高频监测需求（Li et al., 2024a）。
    • 地基 InSAR 具备更高的时空分辨率，但覆盖范围受限，适用于重点区域监测。

---

结论与展望

为解决当前滑坡预测研究的局限性，如对样本点数据的依赖以及对时空特征的忽视，本文提出了一种融合InSAR与STGCN的创新方法。该方法旨在揭示色拉滑坡的变形历史与演化机制，实现金沙江上游色拉地区的全景滑坡预测。研究结果表明，该方法能够有效捕捉整个坡体的复杂时空关系，其预测能力优于传统方法。

通过参数对比实验，我们进一步强调了将物质迁移方向作为空间属性在滑坡预测中的重要性，巩固了STGCN在捕捉时空特征方面的优势。基于本研究的分析，我们预测色拉地区受内外部地质过程的影响，可能发生大规模滑坡。由于色拉滑坡地处金沙江上游，卫星监测数据显示，其滑坡体积可能导致滑坡堵江。一旦发生滑坡堵江事件，在2016年和2018年金沙江水位激增的影响下，堰塞坝溃决可能引发级联式洪水，形成滑坡-洪水灾害的“多米诺效应”，对沿岸基础设施和当地居民构成巨大威胁。

STGCN模型适应性强，可通过较小调整适用于不同地形和滑坡类型。随着计算能力的提升和数据集的不断丰富，该模型在实时监测和大规模滑坡预测方面的潜力将进一步增强。未来研究可结合物理模型与机器学习（如物理引导神经网络（PINN）），引入更多环境变量（如降雨和地震数据），以更全面地描述滑坡的复杂非线性行为（Dahal & Lombardo, 2024; Liu et al., 2024）。

此外，为应对模型的不确定性，未来研究应实施敏感性分析，以深入理解输入参数对预测结果的影响（Liu et al., 2023）。技术手段如蒙特卡洛模拟或贝叶斯网络，可提供更概率化的预测解释，从而量化预测置信度，提升模型的可靠性和透明度。

参考文献
[1] Li Z, Chen J, Cao C, et al. Enhancing long-term prediction of non-homogeneous landslides incorporating spatiotemporal graph convolutional networks and InSAR[J]. Engineering Geology, 2025, 347: 107917.