稀疏高斯过程_稀疏和变分高斯过程数据量大时该怎么办

稀疏高斯过程

Big data is the cure for many machine learning problems. But one person’s cure can be another’s poison. Big data causes many Bayesian methods to be unpractically expensive. We need to do something or Bayesian methods are left behind the big data revolution.

大数据是解决许多机器学习问题的方法。 但是一个人的治愈可能是另一个人的毒药。 大数据导致许多贝叶斯方法不切实际地昂贵。 我们需要做些事情，否则贝叶斯方法将被甩在大数据革命的后面。

In this article, I will explain why big data makes a very popular Bayesian machine learning method — Gaussian Process —unaffordably expensive. Then I will present Bayesian’s solution — the Sparse and Variational Gaussian Process model (SVGP model), that brings Gaussian Process back in the game.

在本文中，我将解释为什么大数据使非常流行的贝叶斯机器学习方法(高斯过程)价格昂贵。 然后，我将介绍贝叶斯解决方案-稀疏和变分高斯过程模型(SVGP模型)，它将高斯过程带回游戏中。

一些符号 (Some notations)

Medium supports Unicode in text. This allows me to write many math subscript notations such as X₁ and Xₙ. But I could not write down some other subscripts. For example:

中号支持文本中的Unicode。 这使我可以编写许多数学下标符号，例如X₁和Xₙ。 但是我无法写下其他一些下标。 例如：

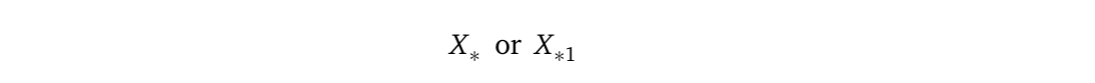
So in the text, I will use an underscore “_” to lead such subscripts, such as X_* and X_*1.

因此，在本文中，我将使用下划线“ _”引导此类下标，例如X_ *和X_ * 1 。

If some math notations render as question marks on your phone, please try to read this article from a computer. This is a known issue with some Unicode rendering.

如果某些数学符号在您的手机上显示为问号，请尝试从计算机上阅读本文。 这是某些Unicode渲染的已知问题。

高斯过程回归模型 (The Gaussian Process regression model)

Suppose we have some training data (X, Y). Both X and Y are float vectors of length n. So n is the number of training data points. We want to find a regression function from X to Y. This is a typical regression task. We can use the Gaussian Process regression model (GPR) to find such a function.

假设我们有一些训练数据(X，Y)。 X和Y均为长度为n的浮点向量。 所以n是训练数据点的数量。 我们想要找到从X到Y的回归函数。 这是典型的回归任务。 我们可以使用高斯过程回归模型(GPR)查找此类函数。

The Gaussian Process regression model is the simplest Gaussian Process model. If you need to refresh your memory, the article Understanding Gaussian Process, The Socratic Way is a great read. This model has two parts — the prior and the likelihood:

高斯过程回归模型是最简单的高斯过程模型。 如果您需要刷新内存，那么这篇文章《 理解高斯过程，苏格拉底式的方式》是一本不错的文章。 该模型有两个部分-先验和可能性：

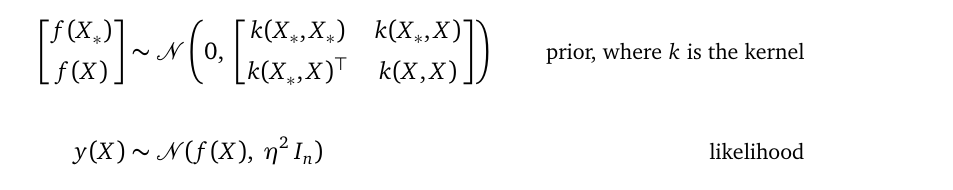
The GP priorThe Gaussian Process prior (GP prior) is a multivariate Gaussian distribution over random variable vectors f(X) and f(X_*):

GP先验高斯过程先验(GP先验)是随机变量向量f(X)和f(X_ *)上的多元高斯分布：

• f(X) is a random variable vector of length n; it represents possible values of the underlying regression function at training locations X.

  f(X)是长度为n的随机变量矢量； 它表示潜在的回归函数在训练位置X的可能值。

• f(X_*) is also a random variable vector. It represents possible values of the underlying regression function at testing locations X_*. Its length n_* depends on how many testing locations you will ask the model to make predictions for. n_* can be very large.

  f(X_ *)也是一个随机变量向量。 它表示在测试位置X_ *的基础回归函数的可能值。 它的长度n_ *取决于您将要求模型进行预测的测试位置数。 n_ *可能非常大。

I will shorten the prior as:

我将先验缩短为：

This multivariate Gaussian distribution has zero mean, and it uses a kernel function k to define its covariance matrix. The covariance matrix k(X, X) is an n×n matrix. You have many choices over the function k, in this article, we use the squared exponential function for k:

此多元高斯分布的均值为零，并且使用核函数k定义其协方差矩阵。 协方差矩阵k(X，X)是n×n矩阵。 您可以对函数k进行多种选择，在本文中，我们对k使用平方指数函数：

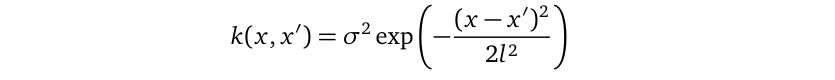
where the signal variance σ² and lengthscale l are model parameters.

其中信号方差σ²和长度标度l是模型参数。

The likelihoodIn the likelihood, y(X) is a random variable vector of length n. It comes from a multivariate Gaussian distribution with mean f(X), and covariance η²Iₙ, where η² is a scalar model parameter called noise variance, and Iₙ is an n×n identity matrix because we assume independent observation noise.

可能性在可能性中， y(X)是长度为n的随机变量矢量。 它来自均值f(X)和协方差η²Iₙ的多元高斯分布，其中η²是称为噪声方差的标量模型参数，而Iₙ是n×n单位矩阵，因为我们假设独立的观察噪声。

Training data Y is modeled as samples of the random variable vector y(X). Since y(X) depends on f(X), we also denote the likelihood as p(y(X)|f(X)). I will use y as a shorthand for y(X), and p(y|f) as the shorthand for the likelihood.

训练数据Y被建模为随机变量向量y(X)的样本。 由于y(X)取决于f(X) ，因此我们也将可能性表示为p(y(X)| f(X)) 。 我将y用作y(X)的简写，并将p(y | f)用作似然的简写。

Since both f and y are multivariate Gaussian random variables, and f is the mean of y, we can rewrite y as a linear transformation from f:

由于f和y都是多元高斯随机变量，并且f是y的均值，我们可以将y重写为f的线性变换：

Then we can apply the multivariate Gaussian linear transformation rule to derive the distribution of y without mentioning the random variable f:

然后我们可以应用多元高斯线性变换规则来得出y的分布，而无需提及随机变量f ：

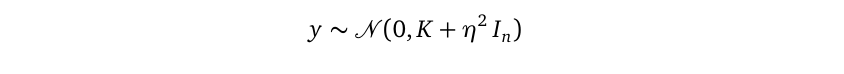
We can write down the probability density function for y:

我们可以写下y的概率密度函数：

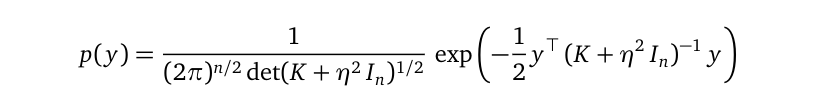
p(y) is the famous marginal likelihood.

p(y)是著名的边际似然。

Parameter learningOur Gaussian Process regression model has three model parameters, lengthscale l, signal variance σ², and observation variance η². We introduced them as part of the modeling process, but we don’t know what concrete values we should set those model parameters to. We use parameter learning to find optimal concrete values for them:

参数学习我们的高斯过程回归模型具有三个模型参数：长度尺度l ，信号方差σ²和观测方差η²。 我们在建模过程中介绍了它们，但是我们不知道应将这些模型参数设置为什么具体值。 我们使用参数学习来找到最佳的具体值：

• “optimal” means that with those concrete values, our model can best explain the training data (X, Y). And,

  “最优”意味着，通过这些具体值，我们的模型可以最好地解释训练数据(X，Y) 。 和，

• “explain the training data”, in the context of probabilistic modeling (which is what we are doing), means how likely the training data is generated by our model, measured by the marginal likelihood p(y).

  在概率建模(这就是我们正在做的事情)的上下文中，“解释训练数据”是指我们的模型以边际可能性p(y)衡量生成训练数据的可能性。

Once the training data X and Y are plugged in, the marginal likelihood p(y) is a function with all the model parameters l, σ², and η². To find optimal values for them, parameter learning uses gradient descent to maximize the objective function log(p(y)) with respect to those model parameters. Here is the formula for the objective function:

一旦插入了训练数据X和Y ，边际似然p(y)就是所有模型参数l，σ²和η²的函数。 为了找到它们的最佳值，参数学习使用梯度下降来相对于那些模型参数最大化目标函数log(p(y)) 。 这是目标函数的公式：

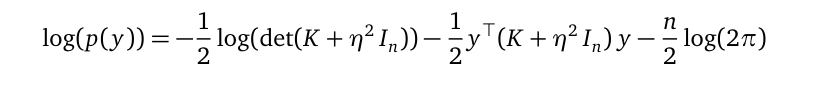
Making predictionsAfter we found optimal values for the model parameters (also known as calibrating the model), we are ready to make predictions. A Gaussian Process model makes predictions using the posterior distribution.

进行预测在找到模型参数的最佳值(也称为校准模型)之后，就可以进行预测了。 高斯过程模型使用后验分布进行预测。

In our Gaussian Process regression model with a Gaussian likelihood, the posterior p(f_*, f|y) has a closed-form analytical expression. To make predictions for f_* at testing locations X_*, we marginalize f out from the posterior:

在具有高斯似然的高斯过程回归模型中，后验p(f_ *，f | y)具有闭合形式的解析表达式。 为了对测试位置X_ *处的f_ *做出预测，我们从后验中将f边缘化：

At line (3), the integrand includes two probability densities — p(f_*|f) and p(f|y). We can derive p(f_*|f) from the GP prior by applying the multivariate Gaussian conditional rule. And the Bayes rule tells us how to compute p(f|y). With its ingredients ready, we can derive the analytical expression for the predictive distribution p(f_*|y):

在第(3)行，被积数包括两个概率密度— p(f_ * | f)和p(f | y) 。 通过应用多元高斯条件规则，我们可以从GP先验得到p(f_ * | f) 。 贝叶斯规则告诉我们如何计算p(f | y)。 准备好其成分后，我们可以得出预测分布p(f_ * | y)的解析表达式：

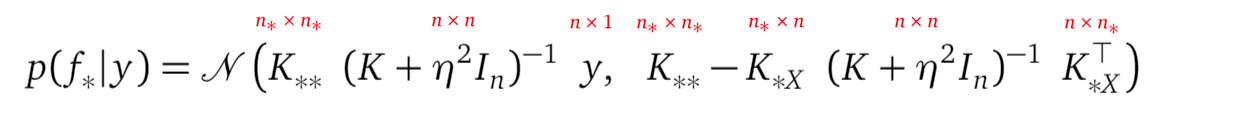
Shapes of the matrices in the above expression are shown in small red notations.

上面表达式中的矩阵形状以红色小符号表示。

Please step to Understanding Gaussian Process, the Socratic Way (the Computing the posterior section) for the full derivations of p(f_*|y).

请逐步理解高斯过程，即苏格拉底式方法 ( 计算后验部分)，以获得p(f_ * | y)的全部推导。

The predictive distribution p(f_*|y) is a distribution over the random variable vector f_*, whose length is n_*. Its structure reveals that in the Gaussian Process regression model, f_* is a linear transformation from y. The model tries to explain f_* using information from y. The kernel (the function k, the training location X, and the testing location X_*) predominantly decides the transformation from y to f_*, with the help from the observation noise η²Iₙ, of course.

预测分布p(f_ * | y)是在长度为n_ *的随机变量矢量f_ *上的分布。 它的结构表明，在高斯过程回归模型中， f_ *是y的线性变换。 该模型尝试使用y中的信息来解释f_ * 。 当然，内核(函数k ，训练位置X和测试位置X_ * )主要决定了从y到f_ *的转换，当然还要借助观察噪声η²Iₙ 。

Please note the number of testing locations n_* can be much larger than the number of training points n. As n_* becomes larger, the matrix K_**, K_*X becomes larger, but the shape of the matrix K+η²Iₙ, which is being inverted, stays the same, n×n.

请注意，测试位置的数量n_ *可能远大于训练点的数量n 。 随着n_ *变大，矩阵K _ ** ， K_ * X变大，但是矩阵K +η²Iₙ的形状被倒置， 保持不变， n×n 。

矩阵求逆的诅咒 (Curse of matrix inversion)

In this Gaussian Process regression model, both the objective function for parameter learning and the predictive distribution mention the matrix inversion (K+η²Iₙ)⁻¹. Matrix inversion is computationally expensive. The number of operations (such as adding, multiplying two numbers) in an n×n matrix inversion scale with n³, with n being the number of data points.

在此高斯过程回归模型中，用于参数学习的目标函数和预测分布都提到了矩阵求逆(K +η²Iₙ)⁻¹ 。 矩阵求逆在计算上是昂贵的。 n×n矩阵求逆标度中的操作数(例如加，乘两个数)为n³，其中n为数据点数。

A Gaussian Process regression model for a dataset with 10,000 data points needs 10¹² operations to invert its covariance matrix. As a comparison, our universe contains 10⁷⁸ to 10⁸² atoms. And a dataset with 10,000 points is just tiny in modern-day standards.

具有10,000个数据点的数据集的高斯过程回归模型需要10 12运算来反转其协方差矩阵。 作为比较，我们的宇宙包含10⁷⁸至10⁸²原子。 在现代标准中，具有10,000点的数据集很小。

(K+σ²Iₙ)⁻¹ is the reason why it is too expensive to apply our Gaussian Process regression model to even a moderate-sized dataset.

(K +σ²Iₙ)⁻¹是将我们的高斯过程回归模型应用于中等大小的数据集过于昂贵的原因。

As an example, here is a dataset with 10,000 points:

例如，这是一个具有10,000点的数据集：

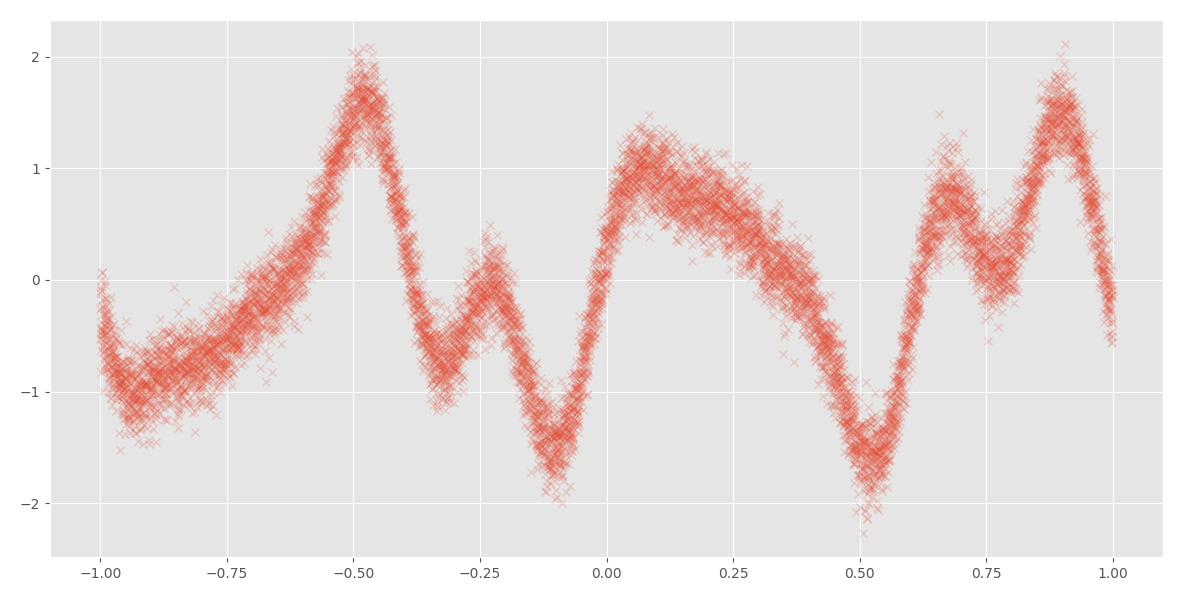
Those small red crosses are data points. When I tried to use this dataset to perform parameter learning for a Gaussian Process regression model, I saw the following warning messages and I waited for hours and then I terminated the program because I didn’t want to wait for it anymore — it is a machine learning model, not my kid, and I don’t have infinite patience for models:

那些小的红叉是数据点。 当我尝试使用此数据集为高斯过程回归模型执行参数学习时，我看到以下警告消息，并且等待了几个小时，然后终止了该程序，因为我不想再等待它了-这是一个机器学习模型，不是我的孩子，而且我对模型没有无限的耐心：

This warning message indicates that the model needs to allocate a lot of memory to perform matrix operations. And the long waiting gives you a vivid impression of the n³ scaling.

此警告消息表明模型需要分配大量内存才能执行矩阵运算。 漫长的等待给您n³缩放的生动印象。

为什么会出现(K + σ²Iₙ ) ⁻¹ ？ (Why does (K+σ²Iₙ)⁻¹ appear?)

The matrix inversion (K+σ²Iₙ)⁻¹ appears in the objective function log p(y) and the predictive distribution because we are using the following factorization from the GP prior:

矩阵求逆(K +σ²Iₙ)⁻¹出现在目标函数对数p(y)和预测分布中，因为我们使用了GP之前的以下因式分解：

• We use the conditional p(f_*|f) part for making predictions because this part links together what we know at training locations (namely f) and what we don’t know at testing locations (namely f_*). See the previous derivation for p(f_*|f).

  我们使用条件p(f_ * | f)进行预测，因为此部分将我们在训练位置(即f )和测试点(即f_ * )所不知道的内容联系在一起。 请参见p(f_ * | f)的先前推导。

• We use the marginal p(f) part, combined with the likelihood p(y|f), for parameter learning because this part links together the random variables whose observations are available (namely y) and the random variables whose observations are not available (namely f). See the previous derivation for p(y).

  我们将边际p(f)部分与似然性p(y | f)结合起来用于参数学习，因为该部分将其观测值可用的随机变量(即y )和其观测值不可用的随机变量(即f )。 参见p(y)的先前推导。

Probability theory allows us to do the above factorization as long as:

概率理论允许我们进行上述分解，只要：

1. p(f_*|f) is a function that mentions both f_* and f; p(f) is a function that mentions f. This makes sure the factorization has the same API as the joint p(f_*, f).

   p(f_ * | f)是同时提及f_ *和f的函数 ； p(f)是提及f的函数。 这样可以确保分解与联合p(f_ *，f)具有相同的API。

2. both p(f_*|f) and p(f) are proper probability density functions. This makes sure that the factorization is still a valid probability density function.

   p(f_ * | f)和p(f)都是适当的概率密度函数。 这样可以确保分解仍然是有效的概率密度函数。

The choice of a multivariate Gaussian distribution as the prior satisfies both requirements, and it makes the derivation of p(f_*|f) and p(f) easy:

选择多元高斯分布作为先验满足这两个要求，并且使p(f_ * | f)和p(f)的推导变得容易：

1. derive p(f_*|f) by applying the multivariate Gaussian conditional rule on the prior.

   通过在先验上应用多元高斯条件规则来推导p(f_ * | f) 。

2. derive p(f) by applying the multivariate Gaussian marginalization rule on the prior.

   通过对先验应用多元高斯边缘化规则来推导p(f) 。

But this factorization planted the unaffordable matrix inversion because the marginal p(f) is a multivariate Gaussian distribution:

但是，由于边际p(f)是多元高斯分布，因此该分解法植入了无法承受的矩阵求逆：

and the K⁻¹ is right there in this probability density function. The marginal likelihood p(y) inherited this inversion and made its own contribution σ²Iₙ, resulting in that unaffordable term (K+σ²Iₙ)⁻¹.

在这个概率密度函数中， K⁻¹就在那里。 边际似然p(y)继承了该反演并做出了自己的贡献σ²Iₙ ，从而导致了该无法承受的项(K +σ²Iₙ)⁻¹。

我们可以降采样吗？ (Can we downsample?)

Since the size of data, n, controls the shape of the covariant matrix K that we have a hard time to invert, can we select a subset of the training data? This is called downsampling. We can, but machine learning practitioners don’t like downsampling because:

由于数据的大小n控制着我们难以转换的协变矩阵K的形状，我们可以选择训练数据的子集吗？ 这称为下采样。 我们可以，但是机器学习从业人员不喜欢下采样，因为：

• It throws away part of the training data. Training data is the most valuable thing in a machine learning task. Throwing part of it away is a sin.
  它会丢弃部分训练数据。 训练数据是机器学习任务中最有价值的东西。 丢掉一部分是一种罪过。
• It is difficult to decide which part of the training data to throw away. Do we downsample equidistantly?
  很难决定丢掉训练数据的哪一部分。 我们是否等距下采样？

我们可以总结训练数据吗？ (Can we summarize the training data?)

Since we don’t want to downsample the training data, but handling the training data is too expensive for us, can we summarize the training data?

由于我们不想对训练数据进行下采样，但是处理训练数据对我们来说太昂贵了，我们可以汇总训练数据吗？

Let’s introduce a new set of random variables f(Xₛ), shortened as fₛ at some locations Xₛ. Xₛ is a vector of scalars of length nₛ. The subscript “ₛ” stands for “sparse”. We don’t know the values of those scalars, they are new model parameters. But we do require nₛ to be much smaller than n— that’s the point of summarization. And we need to choose the value for nₛ, it is not a model parameter.

让我们介绍一组新的随机变量f(Xₛ) ，在某些位置Xₛ简称为fₛ 。 Xₛ是长度为nₛ的标量的向量。 下标“ ₛ”代表“稀疏” 。 我们不知道这些标量的值，它们是新的模型参数。 但是我们确实要求nₛ比n小得多-这就是总结的要点。 我们需要选择nₛ的值，它不是模型参数。

We call Xₛ inducing locations, and fₛ inducing random variables. Don’t ask why. Machine learning people as a group are known to be not great name-givers. Just accept that the names sort of make sense.

我们称Xₛ诱导位置 ，和fₛ诱导随机变量 。 不要问为什么。 众所周知，机器学习人员并不是一个很好的名字提供者。 只需接受名称有意义即可。

At the moment, introducing more random variables into an already expensive model doesn’t seem to be sensible, but please read on, as this turns out to be the key to summarizing all the training data.

目前，将更多随机变量引入本已昂贵的模型中似乎并不明智，但请继续阅读，因为这是总结所有训练数据的关键。

稀疏和变分高斯过程模型 (Sparse and Variational Gaussian Process model)

What do we mean by using fₛ to summarize the training data? Unsurprisingly, we mean that our model should generate the training data with high probability. To achieve that:

用fₛ总结训练数据是什么意思？ 毫不奇怪，我们的意思是我们的模型应该以高概率生成训练数据。 为了达到这个目的：

1. There must be some relationship between fₛ at location Xₛ, and the random variable f at training location X. As usual, the prior of a model establishes this relationship.

   必须有fₛ之间在位置Xₛ并在训练位置X.像往常一样，随机变量f一些关系，在现有的模型的建立这种关系。

2. There needs to be a measure of the probability of the training data given our model. And the likelihood of a model defines this measure.
   给定我们的模型，需要衡量训练数据的概率。 模型的可能性定义了此度量。

稀疏先验 (The sparse prior)

We use a multivariate Gaussian distribution to establish the relationship between fₛ and f as our new prior, which we call the sparse prior because it includes the sparse inducing random variables fₛ:

我们使用多元高斯分布来建立fₛ和f之间的关系作为我们的新先验，我们称其为稀疏先验，因为它包含了稀疏诱导随机变量fₛ ：

which I will shorten as:

我将其简称为：

Please compare the above formula with the old prior from the Gaussian Process regression model, shown here again:

请将上面的公式与高斯过程回归模型中的旧公式进行比较，再次显示如下：

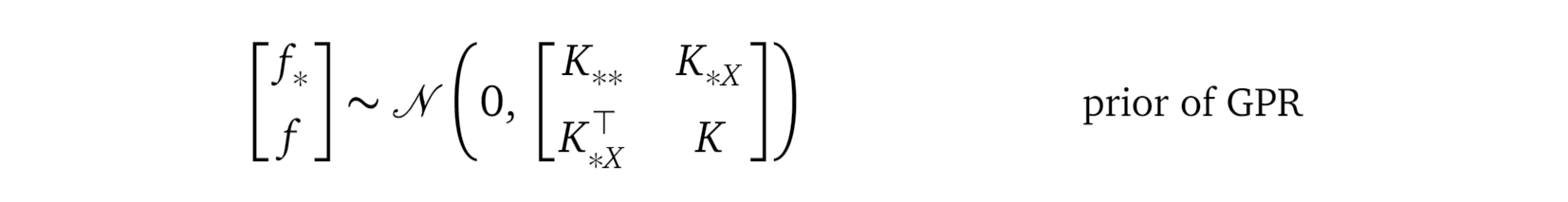
By comparing these two distributions, we realize they have the same structure. This gives us some hint on the intuition behind the inducing variables fₛ:

通过比较这两个分布，我们意识到它们具有相同的结构。 这使我们对归纳变量fₛ的直觉有一些暗示：

• In the SVGP prior, we use fₛ at inducing locations Xₛ to explain f at training locations X. The covariance matrix Kₓₛ defines the correlation between f and fₛ. And the kernel function k defines each entry inside Kₓₛ.

  在SVGP之前，我们在归纳位置Xₛ用fₛ来解释训练位置X的 f 。 协方差矩阵K 1定义f和f 1之间的相关性。 内核函数k定义Kₓₛ中的每个条目。

• In the GPR prior, we use f at training locations X to explain f_* at testing locations X_*. The covariance K_*X defines the correlation between f_* and f. Again, the same kernel function k defines each entry of K_*X.

  在先前的GPR中，我们在训练位置X处使用f来解释测试位置X_ *处的f_ * 。 协方差K_ * X定义f_ *和f之间的相关性。 同样，相同的内核函数k定义K_ * X的每个条目。

Both the SVGP prior and the GPR prior uses the multivariate Gaussian conditional rule as the mechanism to explain one random variable vector from another:

SVGP先验和GPR先验都使用多元高斯条件规则作为从另一个解释一个随机变量向量的机制：

• SVGP uses p(f|fₛ) to explain f from the information of fₛ.

  SVGP使用p(f |fₛ)从fₛ的信息解释f 。

• GPR uses p(f_*|f) to explain f_* from the information of f.

  GPR使用p(f_ * | f)从f的信息解释f_ * 。

归纳变量背后的直觉 (The intuition behind inducing variables)

Realizing the synergy between the SVGP and the GPR priors gives us a definition of what we mean by “using inducing variables to summarize the training data”. The word summarize means “to express the most important facts about something in a short form”. Going back to our SVGP prior:

实现SVGP和GPR先验之间的协同作用，使我们定义了“使用归纳变量总结训练数据”的含义。 摘要一词的意思是“以简短的形式表达某些事物的最重要的事实”。 回到之前的SVGP：

• We use fₛ to express f through the conditional probability density function p(fₛ|f).

  我们使用fₛ通过条件概率密度函数p(fₛ| f)表示f 。

• We require the number of inducing variables nₛ to be smaller (and usually much smaller) than the number of training data points n. This is why the inducing variables summarize the training data. And this is also why we call the SVGP model sparse — we want to use a small number of inducing variables at pivotal inducing locations to explain a much larger number of random variables at training locations.

  我们要求归纳变量nₛ的数量要比训练数据点n的数量小(通常小得多)。 这就是为什么归纳变量总结训练数据的原因。 这也是为什么我们将SVGP模型称为稀疏模型的原因-我们想在枢轴诱导位置使用少量的诱导变量来解释训练位置处的大量随机变量。

The number of inducing variables or locations nₛ is not a model parameter. We need to decide its value. After we have decided on the value for nₛ, we will have a vector Xₛ of length nₛ, representing the locations of those inducing variables. We don’t know where those locations are, they are model parameters, and we will use parameter learning to find concrete values for those inducing locations, along with other model parameters.

归纳变量或位置的数目nₛ不是模型参数。 我们需要确定其价值。 之后，我们决定对nₛ的价值，我们将有长度nₛ的矢量Xₛ，表示这些诱导变量的位置。 我们不知道这些位置在哪里，它们是模型参数，并且我们将使用参数学习来找到这些诱导位置的具体值以及其他模型参数。

You may wonder, why do we assume that we can come up with a good value for the number of inducing locations nₛ, but leave the job of figuring out where those locations are to an optimizer? Because it is easier for us to come up with a single integer number than coming up with nₛ float numbers (or float vectors in case X is multi-dimensional) for the actual locations. We did the same thing when working with a clustering algorithm — we assume we have a good idea of how many clusters are there in the data and let the clustering algorithm to figure out where is the center for each cluster.

您可能想知道，为什么我们假设可以为诱导位置的数量nₛ得出一个很好的值， 却将确定这些位置在哪里的工作留给了优化器呢？ 因为对于实际位置，我们想出一个整数要比想出n个浮点数(或者在X为多维的情况下，浮点向量)要容易得多。 在使用聚类算法时，我们做了同样的事情-假设我们对数据中有多少个聚类有一个很好的了解，然后让聚类算法找出每个聚类的中心在哪里。

SVGP是否应该超过f，fₛ 和f_ *？ (Should the SVGP prior be over f, fₛ and f_*?)

In the above, I wrote the sparse prior to be a joint distribution between f and fₛ. You may ask, shouldn’t this prior include the random variable vector f_* at testing locations X_* as well? Yes, you are right, the full sparse SVGP prior is indeed:

在上面，我将稀疏写为f和fₛ之间的联合分布。 您可能会问，此优先级是否也不应在测试位置X_ *包括随机变量向量f_ * ？ 是的，您是对的，之前的完整稀疏SVGP确实是：

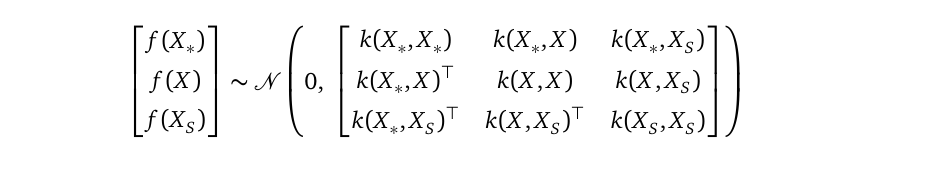
But for the purpose of parameter learning, we can apply the multivariate Gaussian marginalization rule to this full pr