本文深入浅出地探讨了电场强度E、磁场强度H、磁感应强度B和电位移矢量D，以及它们之间的相互关系。通过库仑定律和磁库仑定律，解释电荷和磁荷如何产生电场和磁场。讨论了电极化强度P和磁化强度M的产生原因，并详述了法拉第电磁感应定律和位移电流的概念，揭示了电磁场的本质。
前提
四个物理量的名称：
四个物理量之间的的联系：
1.磁场强度的涡通量是电通量变化率。
2.电通量具有电荷量纲。
3.电荷产生电场强度。
4.电场强度的涡通量是磁通量变化率。
5.磁通量具有磁荷量纲。
6.磁荷产生磁场强度。
两个数学知识
斯托克斯定理：矢量的闭合曲线积分等于闭合曲线内旋度面积分（即闭合曲线内所围涡通量之和）。
高斯定理：矢量的闭合曲面积分等于闭合曲面内散度体积分（即闭合曲面内所围源通量之和）。
电场强度E
现在，有一个电荷
电荷
电荷在电场中受到电场力。
其中
库仑定律
如果有两个点电荷分别带电
库仑力大小
其中，
令
由电场定义式和库仑定律可以轻易得出带电量为
磁场强度H
现在，有一个磁荷
磁荷
磁荷在磁场中受到磁场力
其中
磁库仑定律
如果有两个点磁荷磁单位数值分别为
磁力大小
其中，
令
同上电场的做法，可以求出磁单位为
我们知道，磁荷并不存在。
磁场由电流产生，物质的磁性其实是分子电流的作用，上面各式不过是磁场对于电场的类比。
不过历史上先提出的磁荷理论，导致物理量H占用了名词 “磁场强度（magnetic field intensity）”，真正从电流角度反映磁场的物理量B被称为”磁感应强度（magnetic flux density）“，又称磁通量密度。对应电位移矢量D的另一个名字"电通量密度"
磁感应强度B
现在，有一个电流元
电流元
磁荷在磁场中受到磁场力
其中，
上式的两种常见形式：
安培力：
洛伦兹力：
毕奥-萨伐尔定律
电流元
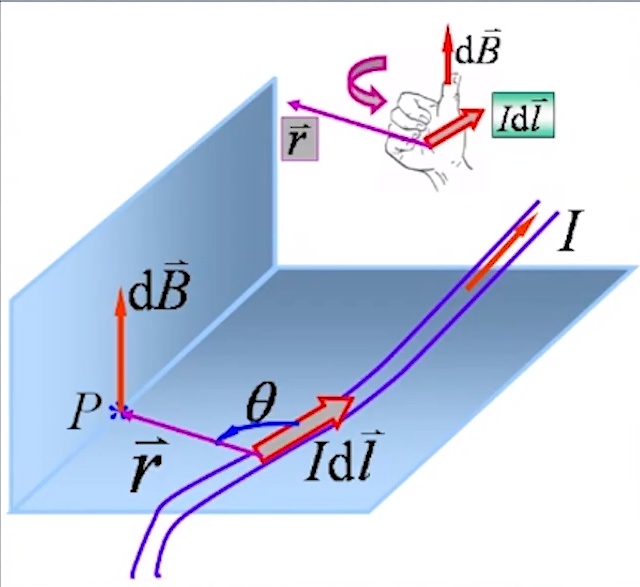
电流元产生的磁场为：
导线产生的磁场为：
L为电流元积分路径，即导线路径。
磁化强度M和电极化强度 P
产生磁化强度M的原因
由于分子电流等原因。磁介质的微观结构具有磁矩。
是磁场或电场下介质的微观结构发生变化而产生的。
无外磁场时，磁介质微观结构排布杂乱无章，总磁矩为0
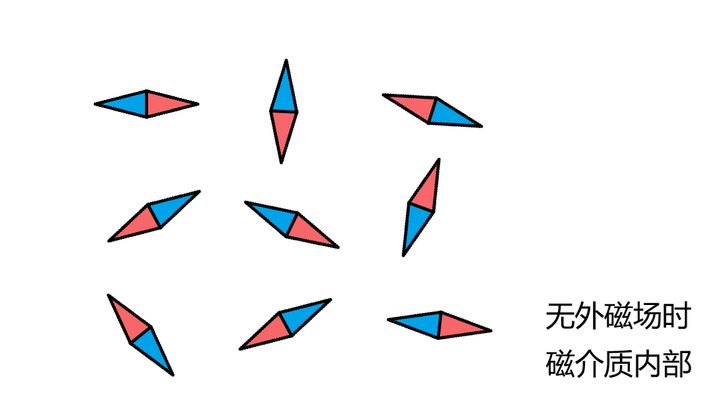
有外磁场时，磁介质微观结构排布整齐，总磁矩不为0。
磁介质内，体积微元
磁化强度
其中，
磁感应强度，磁场强度，磁化强度的关系
结论：磁感应强度除以真空磁导率等于磁场总强度。
ps:
全电流并不全指传导电流。
例如永磁体的磁场由分子电流产生，
变化的电场产生的磁场由位移电流产生。
磁化强度M，磁导率μ
本质上，磁场强度是磁化强度的来源。
顺磁质
磁导率可以理解为磁介质导通磁力线的能力，所以磁感应强度等于磁场强度乘上介质磁导率。
安培环路定理
如果了解
安培环路定理：磁场强度的环路积分等于环路所包围的电流。
其中
我们已经了解到，
即成了我们最开始了解的环路定理公式。
产生电极化强度的原因
电介质的微观结构具有电偶极矩。
无外电场时，电介质微观结构排布杂乱无章，总电偶极矩为0。
有外电场时，电介质微观结构排布整齐，总电偶极矩不为0。
电介质内，体积微元
磁化强度
其中，
电通量密度，电场强度，电极化强度的关系
为了更好理解，我们可以先把电位移矢量叫做电通量密度。
如图所示
电偶极矩
电极化强度除以真空介电常数就是反向极化电场 。即
所以：
结论：电通量密度除以真空介电常数等于原电场的电场强度。
电极化强度数值上等于表面电荷面密度
形式上看， 电极化强度的数值就是Gauss面上电荷密度。
这实际上比较容易理解。
取Gauss面上的某一个电荷，这个电荷为电偶极子的一端。
全Gauss面上电荷为
由于介质本身不带电，Gauss面上却有电荷，Gauss面内必有与Gauss面上等量异号的电荷（实际上这些电荷在点电荷附近），这些异号的电荷即为极化电荷q'。
参考本段公式（2）形式可以看出，电极化强度的数值就是Gauss面上电荷密度。
导体的电极化强度
- 设想导体球壳内有一点电荷q。由于电荷感应，球壳内表面带电-q。在球壳作Gauss面，Gauss面内电荷量为0，球壳上电场强度为0。
- 如果按照电介质处理，把感应电荷看作极化电荷。极化电荷与点电荷电荷量等量异号，所以导体上电极化强度P等于电感应强度D。
- 实际上，Gauss面上电荷密度为0，但球壳外表面有电荷，可以等效在Gauss面上。按照此公式
，电场强度为0，电极化强度却不为0。则电极化率为无穷大。
电极化强度P，介电常数ε
电极化强度与电场强度成正比，且方向相同。
极性物质
介质在外加电场时会产生极化电荷而削弱电场，电场乘以相对介电常数即为原电场。
高斯定理
如果了解
高斯定理：闭合曲面的电通量等于闭合曲面所包围自由电荷的电荷量。
其中
我们已经了解到，
即成了我们最开始了解的高斯定理公式。
麦克斯韦方程组
麦克斯韦方程组由以下四个方程组成，分别是：
- 全电流定律
- 法拉第感应定律
- 高斯磁定律
- 高斯定律
下面是积分形式。
下面是微分形式。
全电流定律
全电流定律反映了电流产生磁场这一现象，由安培环路定律推广而得。
积分形式含义：磁场强度
微分形式含义：磁场强度
这与之前的安培环路定律多了一点内容：全电流，包括传导电流和位移电流。
这个传导电流，即
这个位移电流，即
令
位移电流
电通量变化率为什么是电流？
举一个直观的例子。
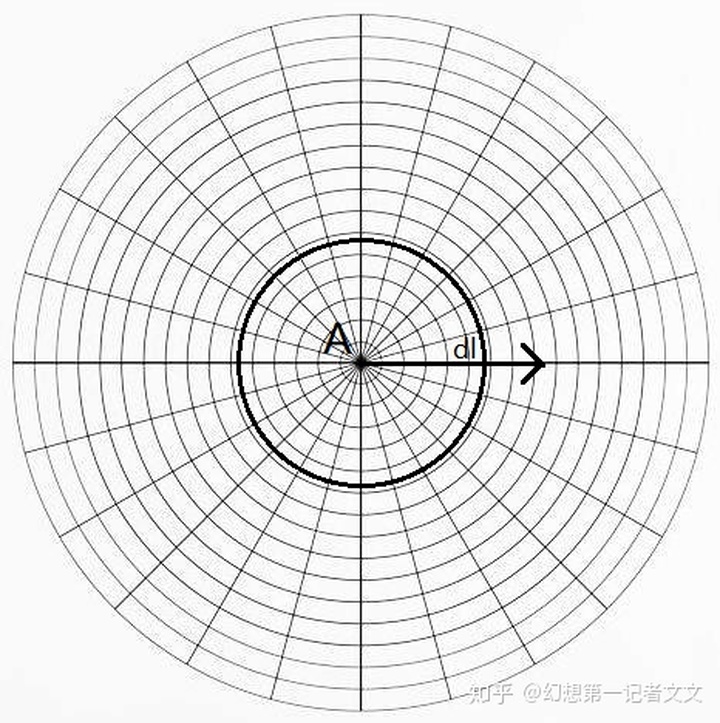
现在，可能理解起来就比较容易了。接下来开始抽象的理解。
我们知道高斯定理：闭合曲面的电通量等于闭合曲面所包围自由电荷的电荷量。
电荷实质上是一个”源“，它向空间中“发散“本身的性质，这个性质实际上是从电荷发出的一条条矢量线。
如果用一个闭合曲面”包住“一些源，那么曲面上就会通过全部这些源发出的矢量线，并且，在闭合曲面外的源产生的矢量线。穿入又穿出闭合曲面，不影响通量。此时，通量就是闭合曲面内部的源。
我们可以假想源分布在闭合曲面上，把通量假想成源，那么通量密度就是源的面密度。使闭合曲面包围的空间趋近于0，那么通量就变成了源。
现在看一般的非闭合曲面。曲面上通过的矢量线由全部源所影响。但实际上，我们仍然可以假想源分布在曲面上。通量假想成源，通量随时间变化即源随时间变化。
电通量具有电荷量量纲，电通量变化率可以看作电荷的变化率，即电流。
位移电流的本质
位移电流是电场随时间变化,引起电位移矢量随时间变化而产生的等效电流，实际上并没有电荷发生移动。并非真实存在。
法拉第电磁感应定律
法拉第电磁感应定律反映了变化的磁场产生电场这一现象。
积分形式含义：穿过曲面的磁通量
微分形式含义：某点的磁感应强度
中学时我们知道的法拉第电磁感应定律应该是这样。
其中，
先解释一个问题。为什么这个法拉第电磁感应定律有一个负号？
其实这个这个问题我们初中就已经解决了，不过可能当时我们记得是另外一条定律。
楞次定律：感应电流具有这样的方向，即感应电流的磁场总要阻碍引起感应电流的磁通量的变化。
这个负号，正是楞次定律所描述内容的表达。
所以，真正的法拉第电磁感应定律应该是这样：
感应电场
1.设想一个闭合回路中间穿过磁场。有一边可以移动。
磁场的方向如图所示，可移动边向右移动，闭合回路内产生逆时针方向的的感应电流。
2.设想一个导体环中间穿过磁场。
磁场的方向如图所示，当磁感应强度变大时，导体环内产生逆时针方向的的感应电流。
以上为感应电动势的两个标准的例子。
感应电动势产生感应电流，而感应电流是实实在在的电流。有电流就意味着存在电荷的移动，这个移动的电荷就是载流子。
分析导体中的一个带有正电荷的载流子。
我们知道，任何物体都要保持匀速直线运动或静止状态，除非有外力迫使它改变运动状态。
实际上，导体电阻不为0，导体中的阻力会使运动的载流子减速直至静止。所以，若不是有外力克服阻力做功，那么不可能保持导体内有电流。
假如闭合回路连接着电池（无体积）会是这样一个过程：正电荷沿导线从正极流向负极，电势降低，电场力克服阻力做功。可以说，此过程，回路中的电流源于电场力。
但是上述例子未连接电池却有电流。如果我们把上述过程克服阻力做功的某个力依然看作是电场力，那么，电荷在某位置受到电场力，意味着此处存在电场。
这个电场就是感应电场。由于载流子在导体环内不断旋转，说明感应电场的电场线是闭合的。
顺便一提，那个连接电池的例子，电池内的过程为：正电荷在电池内从负极流向正极，非静电力克服阻力和电场力做功，电势升高。即使假设电池无体积，整个回路依然是两个过程。电场线并不是闭合的。
实际上，除了感应电场外其他所有的电场线都不是闭合的，所以电场的环路积分除了感应电场以外，其他都等于0。换句话说，所有电场里，只有感应电场的旋度不为0。
所以电场的环路积分就是感应电场的环路积分，即感应电动势。
此方程，就是法拉第电磁感应定律。
p.s.表示电动势应该用大写希腊字母epsilon即Ε表示，为与电场强度E区分，改用小写ε表示。注意区分ε与真空介电常数的表示。
刚才的处理方法是把克服阻力做功的某个力依然看作是电场力，但不能光是“看作”，还要弄明白这个力究竟是什么。
可以从上一段举的两个例子中分析出引起有磁通量变化的原因。
1.动生电场
如例1，磁感应强度不发生变化，但闭合回路的面积发生变化。
回路的面积在变化说明回路正在运动，即发生了切割磁感线。
这个很简单，我们中学就知道，导体切割磁感线产生动生电动势。
导体上的载流子随着导体运动，同时在磁场中受到了洛伦兹力的作用产生的运动，洛伦兹力沿导线方向的分力宏观上使此导体产生电动势。如果导体处在闭合回路上，就会有电流。
所以在例1情况下，克服阻力做功的某个力即洛伦兹力沿导线方向的分力。
2.感生电场
如例2，闭合回路的面积不发生变化，但磁感应强度发生变化。
似乎，磁感应强度随时间变化产生了感应电动势，但是我们还是不知道克服阻力做功的某个力究竟是什么。
当然，这实际上仍然是洛伦兹力的分力。只是解释起来比较复杂。
这并不是理解法拉第电磁感应定律的关键，所以不在此处详细解释。
感应电场的本质
感生电场是一个由洛伦兹力的分力产生的等效电场，实际上并不是电场力的效果。并非真实存在。
高斯磁定律
我们知道磁场是无源场。
积分形式含义：闭合曲面的磁通量等于0。
微分形式含义：空间一点的磁感应强度
根据高斯定理，闭合曲面磁通量应该等于曲面内部包围的磁荷量，因为磁荷不存在，所以等式右边为0。
高斯定理
我们知道电场是有源场。
积分形式含义：闭合曲面的电通量等于曲面包围的电荷量。
微分形式含义：空间一点的电通量密度
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
