1. 特征值和特征向量
左侧A矩阵为m*n的矩阵,其中w为n维的向量,即为特征向量
右侧lambda为特征向量w对应的特征值
基于分解的特征向量和特征值,可以将矩阵A作出以下分解:
2. SVD
2.1 SVD定义
SVD也是对特征值分解,但是和特征值分解不同,SVD分解并不要求被分解的矩阵为方阵,假设我们的矩阵mn的矩阵,那么定义矩阵的SVD为如下:
其中U是一个mm的矩阵,
是一个mn的矩阵,除了主对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值,
V是一个nn的矩阵。
U和V都是酉矩阵,即满足
下图可以很形象的看出上面SVD的定义:
2.2. SVD计算
2.3. SVD的一些性质
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。
也就是说,我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。
由于这个重要的性质,从直观的看,就可以发现SVD可以用于做数据压缩和去噪。比如做图像的压缩。
2.4. python 实现:
import numpy as np
A = np.array([[2, 4], [1, 3], [0, 0], [0, 0]])
print(np.linalg.svd(A))
3 PCA


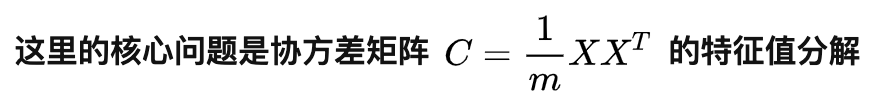
6.SVD与PCA对比
PCA理解和含义
PCA的问题其实是一个基的变换,使得变换后的数据有着最大的方差。
我们用于机器学习的数据(主要是训练数据),方差大才有意义,不然输入的数据都是同一个点,那方差就为0了,这样输入的多个数据就等同于一个数据了。
对原始的空间中顺序地找一组相互正交的坐标轴,第一个轴是使得方差最大的,第二个轴是在与第一个轴正交的平面中使得方差最大的,第三个轴是在与第1、2个轴正交的平面中方差最大的,这样假设在N维空间中,我们可以找到N个这样的坐标轴,我们取前r个去近似这个空间,这样就从一个N维的空间压缩到r维的空间了,但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。
SVD推导PCA
SVD其实是两个方向上的PCA
PCA是对AA ^T的分解
而SVD是:U的列是AAT的特征向量,V的列是AT*A的特征向量
也可以通过SVD分解公式,利用求得得V求解 U(如上面手推求解答的案例
PCA在特定条件下可以转换为SVD求解,那转化为SVD问题有什么好处?
有三点:
一般X的维度很高,ATA的计算量很大
方阵的特征值分解计算效率不高
SVD除了特征值分解这种求解方式外,还有更高效且更准确的迭代求解法,避免了ATA的计算
有了SVD就可以得到两个方向的PCA。
注意到PCA仅仅使用了我们SVD的右奇异矩阵,没有使用左奇异矩阵。
而左奇异矩阵可以用于行数的压缩,即去噪
右奇异矩阵可以用于列数,也就是PCA降维。
参考:https://blog.csdn.net/jiayalu/article/details/100533184








![[公式]](https://img-blog.csdnimg.cn/5189661d7599428091cb84932c4b7a7d.png)
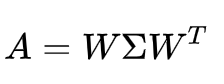
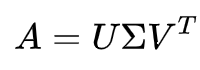
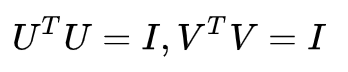

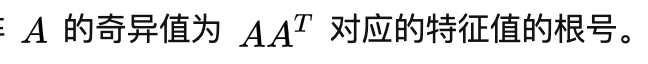
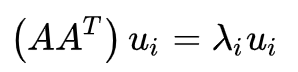
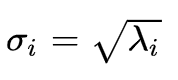

















 3627
3627











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








