基于Matlab的飞行机械臂耦合动力学建模是一个复杂的过程,需要综合考虑飞行器和机械臂的动力学特性。以下是一些基本步骤和方法:
### 1. 建立飞行器动力学模型
首先,需要建立飞行器的基本动力学模型。飞行器的运动可以通过刚体动力学方程来描述,包括平移运动和旋转运动。
```matlab
% 飞行器质量
m = 1.0;
% 飞行器惯性矩阵
I = [0.02, 0, 0;
0, 0.02, 0;
0, 0, 0.04];
% 位置向量
r = [0; 0; 0];
% 速度向量
v = [0; 0; 0];
% 姿态四元数
q = [1; 0; 0; 0];
% 角速度向量
omega = [0; 0; 0];
% 力
F = [0; 0; 0];
% 力矩
M = [0; 0; 0];
% 动力学方程
dr_dt = v;
dv_dt = F / m;
dq_dt = 0.5 * quatmultiply(q, [0; omega]);
domega_dt = I \ (M - cross(omega, I * omega));
% 时间步长
dt = 0.01;
% 仿真时间
T = 10;
% 仿真步数
N = T / dt;
% 初始化状态向量
state = [r; v; q; omega];
% 仿真循环
for i = 1:N
% 更新状态
state = state + dt * [dr_dt; dv_dt; dq_dt; domega_dt];
% 更新力和力矩
F = [0; 0; m * 9.81]; % 重力
M = [0; 0; 0];
% 更新导数
dr_dt = state(4:6);
dv_dt = F / m;
dq_dt = 0.5 * quatmultiply(state(7:10), [0; state(11:13)]);
domega_dt = I \ (M - cross(state(11:13), I * state(11:13)));
end
```
### 2. 建立机械臂动力学模型
接下来,建立机械臂的动力学模型。机械臂的运动可以通过多刚体动力学方程来描述。
```matlab
% 机械臂关节角度
theta = [0; 0];
% 关节角速度
dtheta = [0; 0];
% 关节角加速度
ddtheta = [0; 0];
% 关节力矩
tau = [0; 0];
% 机械臂质量矩阵
M_arm = [1, 0; 0, 1];
% 机械臂科氏力和离心力
C_arm = [0, 0; 0, 0];
% 机械臂重力项
G_arm = [0; 0];
% 动力学方程
ddtheta = M_arm \ (tau - C_arm * dtheta - G_arm);
% 仿真循环
for i = 1:N
% 更新关节角度和角速度
theta = theta + dt * dtheta;
dtheta = dtheta + dt * ddtheta;
% 更新关节力矩
tau = [0; 0];
% 更新关节角加速度
ddtheta = M_arm \ (tau - C_arm * dtheta - G_arm);
end
```
### 3. 耦合动力学模型
将飞行器和机械臂的动力学模型进行耦合,得到完整的系统动力学模型。
```matlab
% 耦合后的质量矩阵
M_total = [m * eye(3), zeros(3, 3);
zeros(3, 3), I];
% 耦合后的科氏力和离心力
C_total = [zeros(3, 3), zeros(3, 3);
zeros(3, 3), -cross(omega, I * omega)];
% 耦合后的重力项
G_total = [m * 9.81; 0; 0];
% 耦合后的动力学方程
state = [r; v; q; omega; theta; dtheta];
dr_dt = v;
dv_dt = F / m;
dq_dt = 0.5 * quatmultiply(q, [0; omega]);
domega_dt = I \ (M - cross(omega, I * omega));
ddtheta = M_arm \ (tau - C_arm * dtheta - G_arm);
% 仿真循环
for i = 1:N
% 更新状态
state = state + dt * [dr_dt; dv_dt; dq_dt; domega_dt; dtheta; ddtheta];
% 更新力和力矩
F = [0; 0; m * 9.81]; % 重力
M = [0; 0; 0];
tau = [0; 0];
% 更新导数
dr_dt = state(4:6);
dv_dt = F / m;
dq_dt = 0.5 * quatmultiply(state(7:10), [0; state(11:13)]);
domega_dt = I \ (M - cross(state(11:13), I * state(11:13)));
ddtheta = M_arm \ (tau - C_arm * dtheta - G_arm);
end
```
### 解释
1. **飞行器动力学模型**:描述了飞行器的平移和旋转运动。
2. **机械臂动力学模型**:描述了机械臂的关节运动。
3. **耦合动力学模型**:将飞行器和机械臂的动力学模型进行耦合,得到完整的系统动力学模型。
通过上述步骤,可以建立一个基于Matlab的飞行机械臂耦合动力学模型。


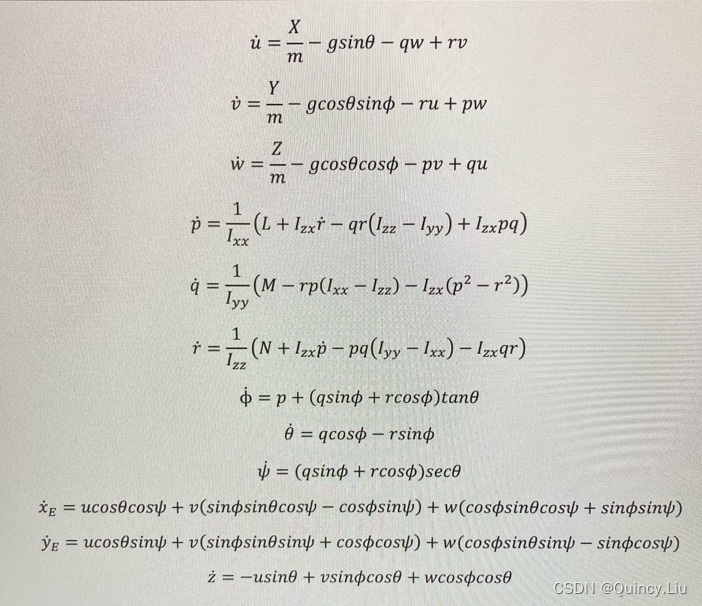

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


