水平有限,如有错误恳请指正。
目录
相位与增益
在任意频率下,一个正弦波输入总是产生一个正弦波输出,输入与输出之间可能的差别仅在于相位与增益。
相位:用于描述输入与输出之间的时间移动。延迟可以用时间Tdelta表示,但更多是用度表示。
![]()
增益:用于测量输入与输出的幅值之间的差异,用分贝或dB表示。
![]()
相位与增益可由传递函数计算出
![]()
示例:输入正弦波1V,10Hz,输出0.7V,延迟12.5ms,则

示例:求输入信号10Hz的低通滤波器传递函数的相位与增益

控制系统性能分析
响应速度分析和稳定性分析,都采用阶跃响应进行测量。因为阶跃响应有丰富的高频成分,它有因陡峭的边沿带来的高频分量,也有边沿之间数值恒定所表征的低频分量,是一个在大频率范围内的激励系统。

响应速度分析
在时域,测量系统跟随指令信号的速度,通过分析阶跃响应的建立时间。建立时间(上升时间)表示从阶跃的初始值到目标值的95%或98%时刻之间的时间。
在频域,测量系统跟随指令信号的速度,通过分析阶跃响应的闭环系统伯德图增益,增益越大,响应速度越快。多数控制系统,在低频段指令响应良好,但是在高频段反应迟钝。在低频段,控制器有足够快的速度调节系统,但是随着频率的增加,控制器跟不上。从传递函数的角度,在低频段增益接近1,但是在高频段增益远小于1。
在频域,常用带宽来度量闭环系统的响应速度,与带宽对应的频率,增益下降到-3dB或下降到原来增益的70%,带宽越大,响应速度越快。系统的时间常数近似表示为

其中,时间常数的单位秒,fB带宽的单位Hz。
稳定性分析
在时域,测量系统的稳定性,通过分析阶跃响应的超调量。超调量表示系统的最大值减去稳态值与稳态值的比再乘100%。实际应用中,超调量可接受范围0-30%。

在频域,测量系统的稳定性,通过分析阶跃响应的闭环系统伯德图增益。多数系统,在低频段的增益为0dB,随着频率的增加,增益减小。如果增益在开始减小前增大了,这种现象称为凸峰,表明系统临界稳定。实际应用中,凸峰值可接受范围0-4dB。
仿真示例
以PI控制的无静差直流调速系统为例,对其响应速度和稳定性进行分析。
1、在Matlab的Simulink仿真中绘制控制系统仿真图,设置两组对照组,一组Kp=Ki=0.05,另一组Kp=Ki=0.01。

2、响应速度分析,时域分析,将仿真输入放到示波器中观察,增益系数为0.05的系统上升时间更短,响应速度更快。


3、响应速度分析,频域分析,生成闭环系统伯德图,选择输入,右键Linear Analysis Points->Input Perturbation;选择输出,右键Linear Analysis Points->Output Measurement;选择分析,Analysis->Control Design->Linear Analysis。增益0.05时,带宽为6.98Hz;增益为0.01时,带宽为1.22Hz,所以增益0.05响应速度更快。




4、稳定性分析,时域分析,比较增益0.05和0.5的系统稳定性,从示波器波形的超调量可以看出,增益0.5超调量为65%,增益0.05超调量为10%,所以增益0.05更稳定。


5、稳定性分析,频域分析,比较增益0.05和0.5的系统稳定性,从闭环系统伯德图的凸峰值可以看出,增益0.5凸峰值为12.8dB,增益0.05凸峰值为0dB,所以增益0.05更稳定。

稳定裕度
增益穿越频率:开环伯德图增益通过0dB时的频率。
相位穿越频率:开环伯德图相位通过-180°时的频率。
对于开环增益K=1(20lgK=0dB)的系统,相位滞后180°时,系统从期望的负反馈变成正反馈,系统不稳定。即在相位为-180°时,只要开环增益远大于0dB或远小于0dB,系统稳定。
相位裕度(Phase Margin,PM),增益穿越频率对应的相位与-180°之差。
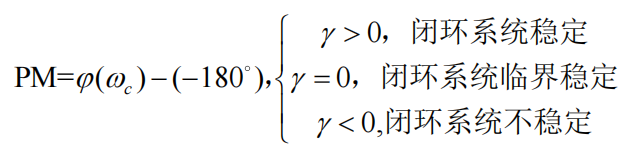
增益裕度(Gain Margin,GM),相位穿越频率对应的增益与0dB之差。

工程经验表明,相位裕度PM范围35°到80°,增益裕度GM范围10dB到25dB,具体根据控制器类型进行分析,相位裕度PM和增益裕度GM越大越好,这样可以消除没必要的相位滞后。
参考文献
《Control System Design Guide》George Ellis










 本文探讨了控制系统中的性能分析,包括响应速度(通过阶跃响应和带宽衡量)和稳定性(通过超调量和凸峰值)。以PI控制的直流调速系统为例,通过MatlabSimulink仿真,对比不同增益系数下的响应速度和稳定性。相位裕度和增益裕度对系统稳定性的重要性也得到强调。
本文探讨了控制系统中的性能分析,包括响应速度(通过阶跃响应和带宽衡量)和稳定性(通过超调量和凸峰值)。以PI控制的直流调速系统为例,通过MatlabSimulink仿真,对比不同增益系数下的响应速度和稳定性。相位裕度和增益裕度对系统稳定性的重要性也得到强调。

















 757
757

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










