【Input Shaping】输入整形

置顶奶油芝士汉堡包

已于 2024-11-29 19:39:32 修改

阅读量6.3k

点赞数 50

分类专栏：控制算法文章标签：输入整形 Input Shaping

于 2024-05-03 12:01:46 首次发布

本文链接：https://blog.csdn.net/weixin_41276397/article/details/138393849

版权

控制算法专栏收录该内容

10 篇文章

订阅专栏

有朋友问我要Matlab的仿真代码，放在文章最后面。欢迎学习和交流~~

水平有限，如有错误，恳请指正。

振动和振动抑制

振动是指物体或结构随时间变化在其平衡位置附近做往复运动，通常用位移、速度和加速度描述。

振动抑制是对系统的动态响应或不稳定性加以控制，把系统振动水平限制在允许的范围内。振动抑制的控制方法分为被动控制和主动控制。主动控制又分为开环控制、闭环控制和非线性控制等。

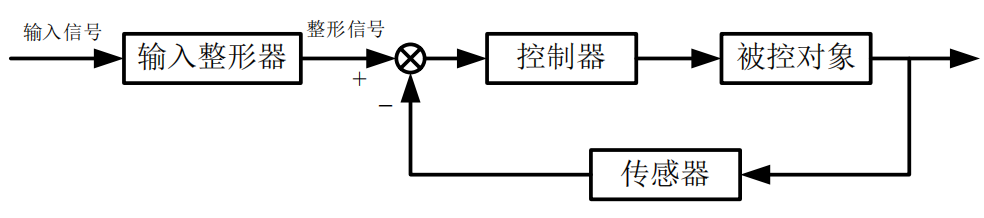
输入整形器基本原理

如果直接驱动系统到被控对象的目标值，被控对象不能立即定位在目标位置上，由于振动模态的存在，被控对象将产生振动。

将被控对象分成若干段（分段处理），以2个脉冲的输入整形器为例，从0时刻开始，在t1时刻，给系统一个脉冲信号，产生了幅值为A1的振动，在t2时刻，又给系统一个脉冲信号，产生了幅值为A2的振动，这两个振动响应幅值大小相等，方向相反，两个振动相互抵消，则到达目标位置时，被控对象不存在振动，立即定位到目标位置。

输入整形定义

输入整形（Input Shaping）用于减少振动，是一项开环的前馈控制技术，其作法是产生一系列脉冲信号来消除其自身的振动。

输入整形将脉冲信号和输入信号进行卷积，接着用整形后的信号来控制系统。脉冲的振幅以及时滞时间会依照系统的特性即自然振动频率和阻尼比决定。

输入信号整形的优缺点

优点：只需要对输入指令进行整形就可以消除减少震动，不需要反馈传感器，避免了增加阻尼、提高刚度而引起的结构质量增加，成本低、结构简单、容易实现。

缺点：引入时间延时，产生滞后。

输入整形器设计

n个脉冲的输入整形器的时域表达式为：

经过拉普拉斯变换后，输入整形器的频域表达式为：

由时域及频域表达式观察知，输入整形器设计的关键是确认整形器脉冲个数n，以及确认用于抑制振动的每个脉冲幅值A和对应的时滞t。

输入整形器的设计方法包括零极点对消法、脉冲响应法、灵敏度曲线法、联立约束方程法。

零极点对消法，通过增加适当的零点或极点来抵消系统中存在的不理想的零点（反映系统快速性）或极点（反映系统稳定性），以此改善系统的频率响应或稳定性。脉冲响应法，从时域的角度说明输入整形器能抑制振动的特性。灵敏度曲线法，通过对不敏感度的定义，对输入整形器的鲁棒性起到了量化衡量作用，并能预测可能激发的模态。联立约束方程法，根据一定的期望特性采用不同的约束方程来推导不同类型的输入整形器，即根据残余振动百分比方程，再添加一些新的约束方程，如鲁棒性约束方程、幅值约束方程和时滞约束方程等共同求解期望的输入整形器。

零极点对消法

下面以零极点对消法为例，设计输入整形器。二阶系统的两个闭环极点（一对共轭复极点），周围没有闭环零点，且所以为闭环主导极点，通过配置输入整形器的零点，实现零极点对消，使系统稳定不振动。

任意的线性高阶系统都可以简化为二阶系统，则二阶系统的传递函数表示为：

二阶系统的特征方程为：

二阶系统的特征根极点为：

当 $0< \xi <1$ 时，系统为欠阻尼，则二阶系统的有一对实部为负的共轭复极点：

当系统输入信号为单位脉冲函数时，系统的响应为单位脉冲响应，二阶系统的单位脉冲响应为：

则二阶欠阻尼系统的单位脉冲响应为：

令

带入输入整形器的频域表达式（传递函数），根据欧拉公式对其分解，并令其为零。

令实部和虚部分为为0。

如果输入整形器的幅值和时滞满足上面两个公式，则可以抑制二阶系统振动。

残余振动

加入输入整形器前，t时刻单位脉冲输出为：

加入输入整形器后，t时刻单位脉冲输出为：

残余振动（Residual Vibration）为表示为输入整形器加入前后的输出幅值之比。C和S可以看作上述零极点对消法中的实部和虚部。

输入整形器类别

输入整形器推导结果可能是无数个，所以要增加约束条件，获得唯一解。

幅值约束条件，保证增益在输入整形前后幅值相同。如果系统不发生超调，幅值应该全为正数。

时滞约束条件，选择尽可能小的时滞时间，设置第一个脉冲在0时刻。

零振动整形器ZV

零振动整形器（Zero Vibration Shaper），有两个脉冲n=2。

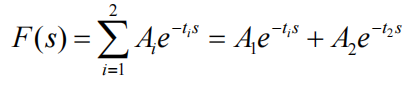
ZV输入整形器约束条件：

计算整形器的幅值和时滞：

令时滞最小，则k=1，得到时滞t2

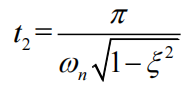
将t2带回约束条件，得到幅值A1和A2

ZV输入整形器的幅值和时滞：

零振动一阶微分整形器ZVD

零振动一阶微分整形器（Zero Vibration and Derivative Shaper），有3个脉冲，当模型参数很准确时，ZV整形器能很好的抑制残余振动，但当模型参数不准确时，ZV整形器的零点不能有效的对消系统的零点，从而不能有效的消除残余振动。为了增强输入整形器对振动抑制的鲁棒性，对残余振动进行约束，除了ZV输入整形器的约束条件，增加对固有频率的微分，并使其为0。

ZVD输入整形器约束条件：

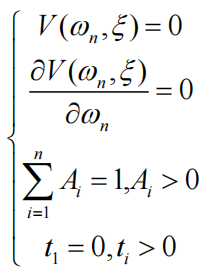
$V(\omega _{n},\xi )$ 对 $\omega _{n}$ 求一阶导数，，经过化简可得：

$V(\omega _{n},\xi )$ 对 $\omega _{n}$ 求n阶导数，，经过化简可得：

上式，q为求导次数，增加1次导数，会多1个脉冲数，时滞增加，但是鲁棒性得到改善。

推导过程可以参考ZV输入整形器，这里不再进行推导。

ZVD输入整形器的幅值和时滞：

零振动二阶微分整形器ZVDD

零振动二阶微分整形器（Zero Vibration Derivative Derivative Shaper），有4个脉冲，相比ZVD提高了输入整形器的鲁棒性。

ZVDD输入整形器约束条件：

ZVDD输入整形器的幅值和时滞：

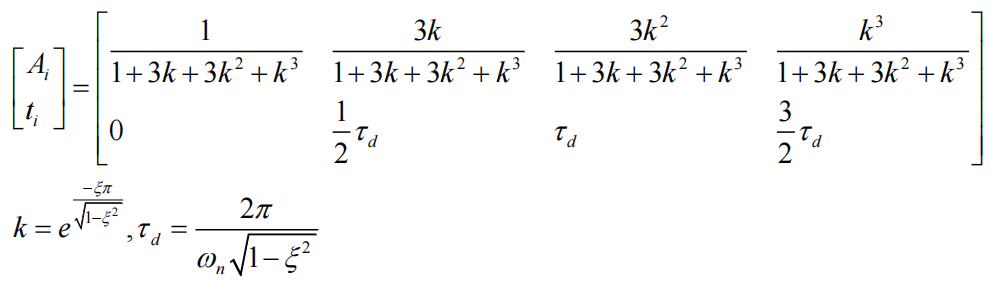
零振动三阶微分整形器ZVDDD

零振动三阶微分整形器（Zero Vibration Derivative Derivative Derivative Shaper），有5个脉冲，相比ZVDD进一步提高了输入整形器的鲁棒性，同时也增加了时滞。

ZVDDD输入整形器约束条件：

ZVDDD输入整形器的幅值和时滞：

单峰极不灵敏整形器EI-1hump

极不灵敏整形器（Extra Insensitivity Shaper），有3个脉冲，不要求在系统固有频率点处振动为零，只需在固有频率附近处使系统的残余振动小于或等于允许的最大残余振动值Vtol，在模型频率 $\omega _{n}$ 左右两侧分别取两个频率 $\omega _{l}$ 和 $\omega _{h}$ ，使输入整形抑制系统摆动的频率范围变广，增强了输入整形器的鲁棒性。

EI输入整形器约束条件：

当 $\xi \neq 0$ 时，，该约束条件方程组没有解析解，对于确定的阻尼系数和最大残余振动Vtol，可以用mathematica等数学软件求数值解。

EI输入整形器的幅值和时滞：

当 $\xi =0$ 时，EI整形器是以 $\omega _{n}$ 为中心对称的的灵敏度曲线。

无阻尼EI输入整形器的幅值和时滞：

双峰极不灵敏整形器EI-2hump

双峰极不灵敏整形器（Two-hump Extra Insensitivity Shaper），有4个脉冲，相比EI进一步提高了输入整形器的鲁棒性，同时也增加了时滞。

无阻尼EI-2hump输入整形器的幅值和时滞：

三峰极不灵敏整形器EI-3hump

三峰极不灵敏整形器（Three-hump Extra Insensitivity Shaper），有5个脉冲，相比EI-2hump进一步提高了输入整形器的鲁棒性，同时也增加了时滞。

无阻尼EI-3hump输入整形器的幅值和时滞：

改进零振动整形器MZV

改进零振动整形器（Modified Zero Vibration Shaper），意在减少时滞的同时增强鲁棒性。当脉冲数为2个，MZV表示为ZV整形器。

N个脉冲MZV输入整形器的幅值和时滞：

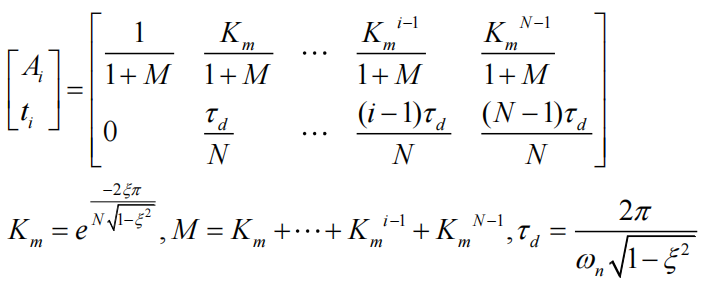
MZV-3impulse输入整形器的幅值和时滞：

MZV通过卷积任意2个MZV整形器得到MZVD整形器，当2个脉冲的MZV整形器和2个脉冲的MZV整形器卷积得到3个脉冲的MZVD整形器（即ZVD整形器），当2个脉冲的MZV整形器和3个脉冲的MZV整形器卷积得到6个脉冲的MZVD整形器。

MZV-2_3impulse输入整形器的幅值和时滞：

输入整形器分析

快速性分析

时域分析，用于分析输入整形器的快速性。分析调节时间的大小，时间越小越好。假设系统的固有频率为30，阻尼比为0.05。

1.实际频率=系统频率，实际阻尼比=系统阻尼比。

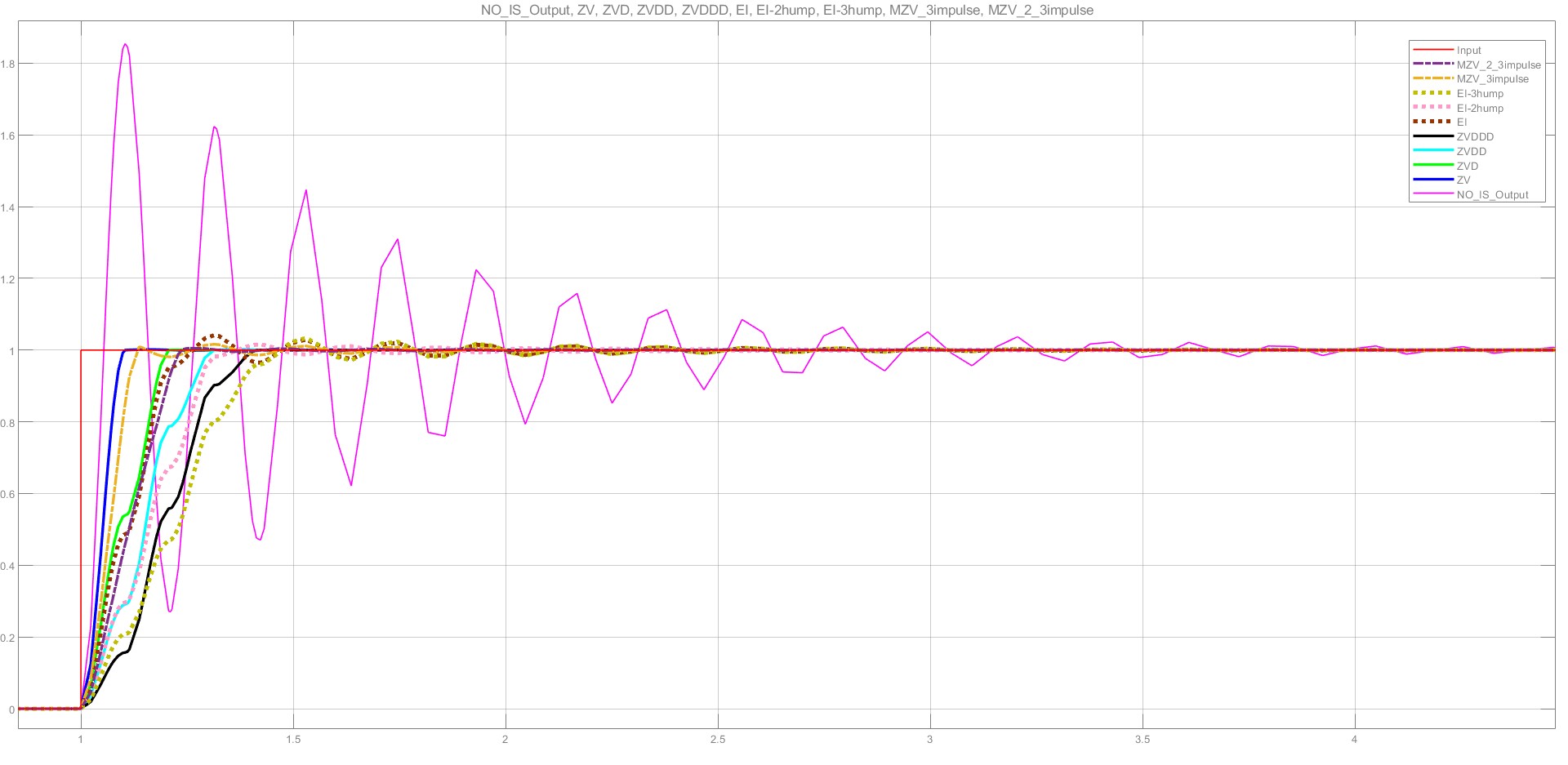
从左往右，调节时间依次增大（ZV最小，EI-3hump最大）
ZV	MZV_3impulse	ZVD	MZV_2_3impulse	EI	ZVDD	EI-2hump	ZVDDD	EI-3hump

2.实际频率取50，实际频率>系统频率，实际阻尼比=系统阻尼比。

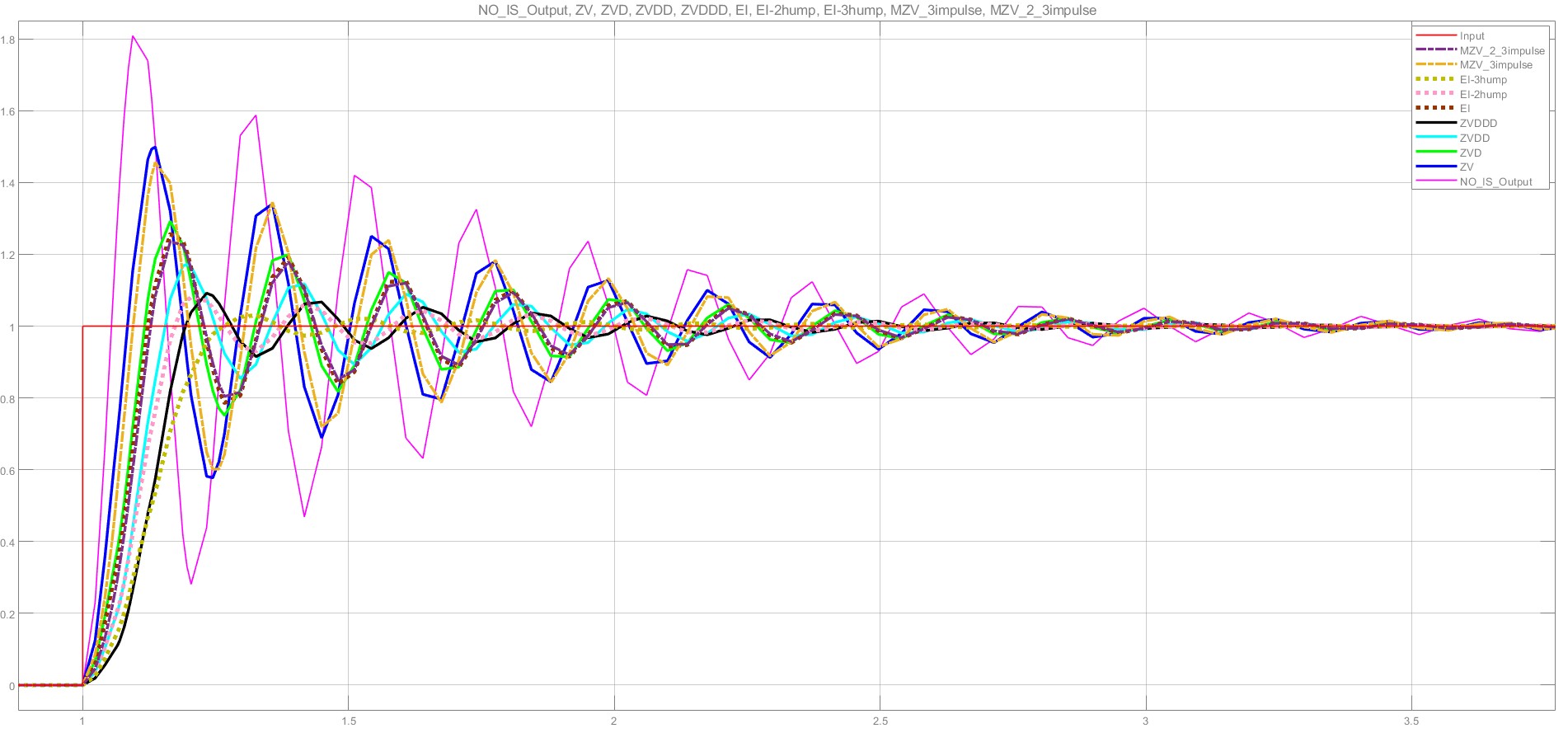
从左往右，调节时间依次增大（EI-3hump最小，MZV_3impulse最大）
EI-3hump	ZVDDD	EI-2hump	ZVDD	MZV_2_3impulse	EI	ZVD	ZV	MZV_3impulse

3.实际频率取10，实际频率<系统频率，实际阻尼比=系统阻尼比。

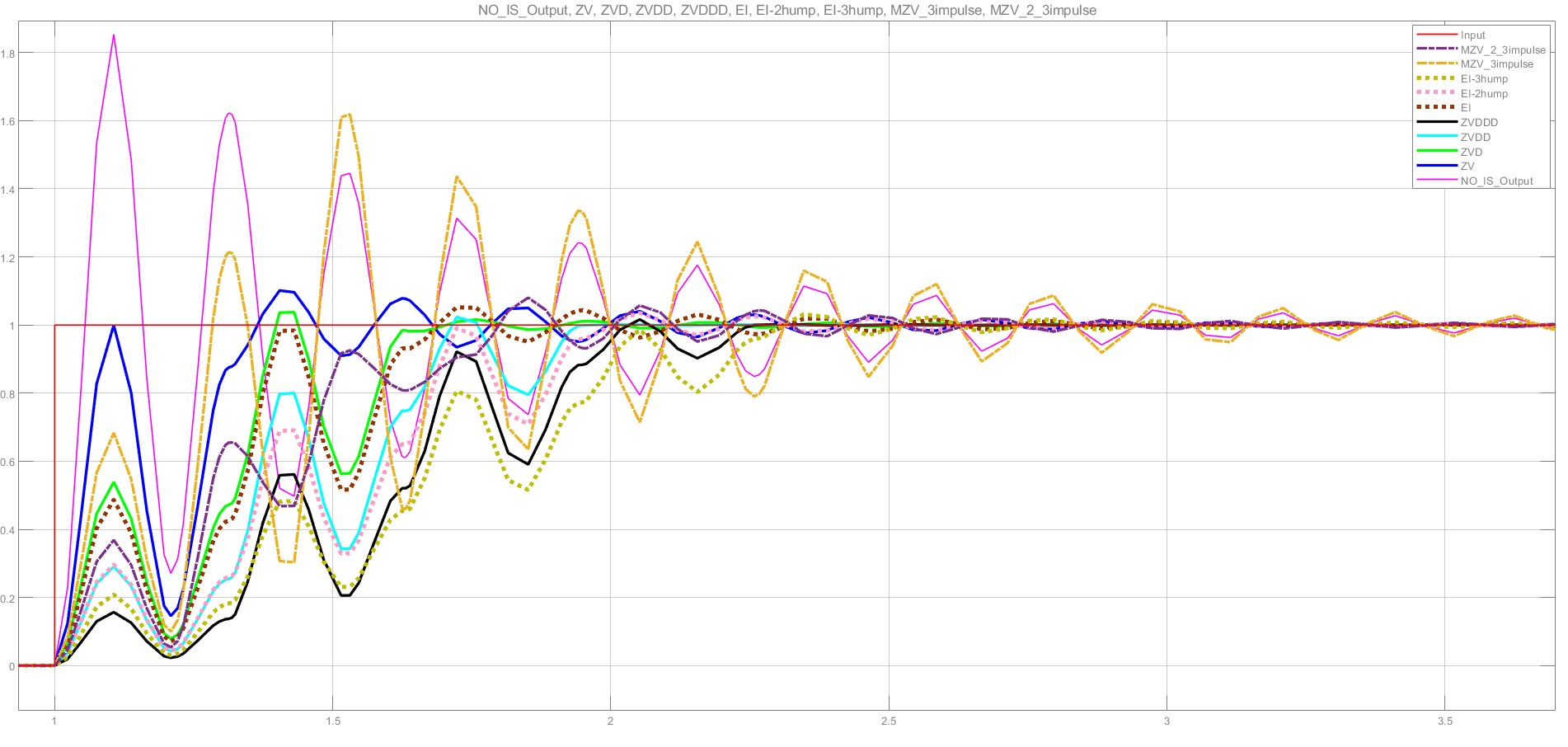
从左往右，调节时间依次增大（ZVD最小，MZV_3impulse最大）
ZVD	ZVDD	ZVDDD	EI	EI-2hump	ZV	EI-3hump	MZV_2_3impulse	MZV_3Impulse

4.实际阻尼比取0.1，实际频率=系统频率，实际阻尼比>系统阻尼比。

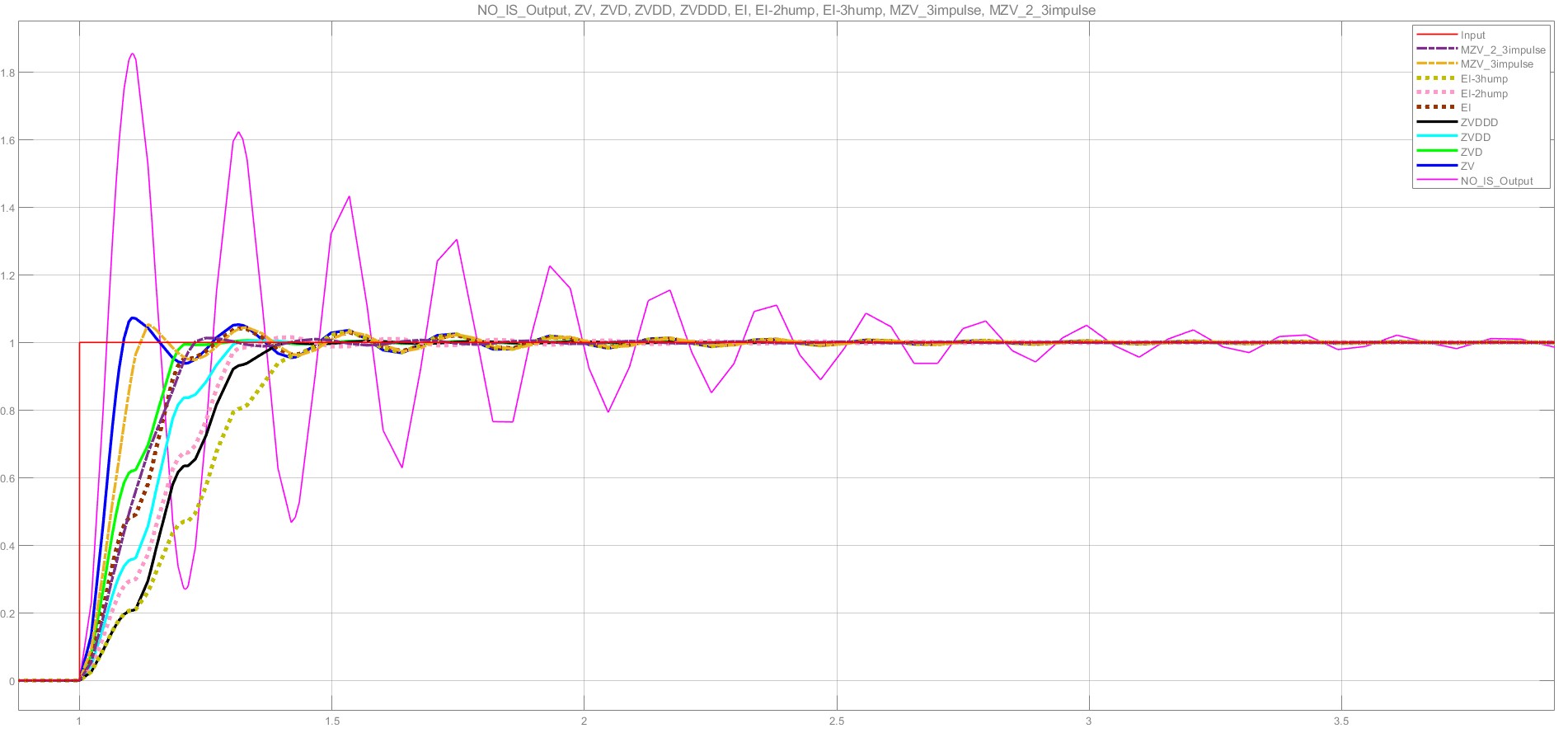
从左往右，调节时间依次增大（ZVD最小，ZV最大）
ZVD	MZV_2_3impulse	ZVDD	ZVDDD	EI-2hump	EI	EI-3hump	MZV_3impulse	ZV

5.实际阻尼比取0.01，实际频率=系统频率，实际阻尼比<系统阻尼比。

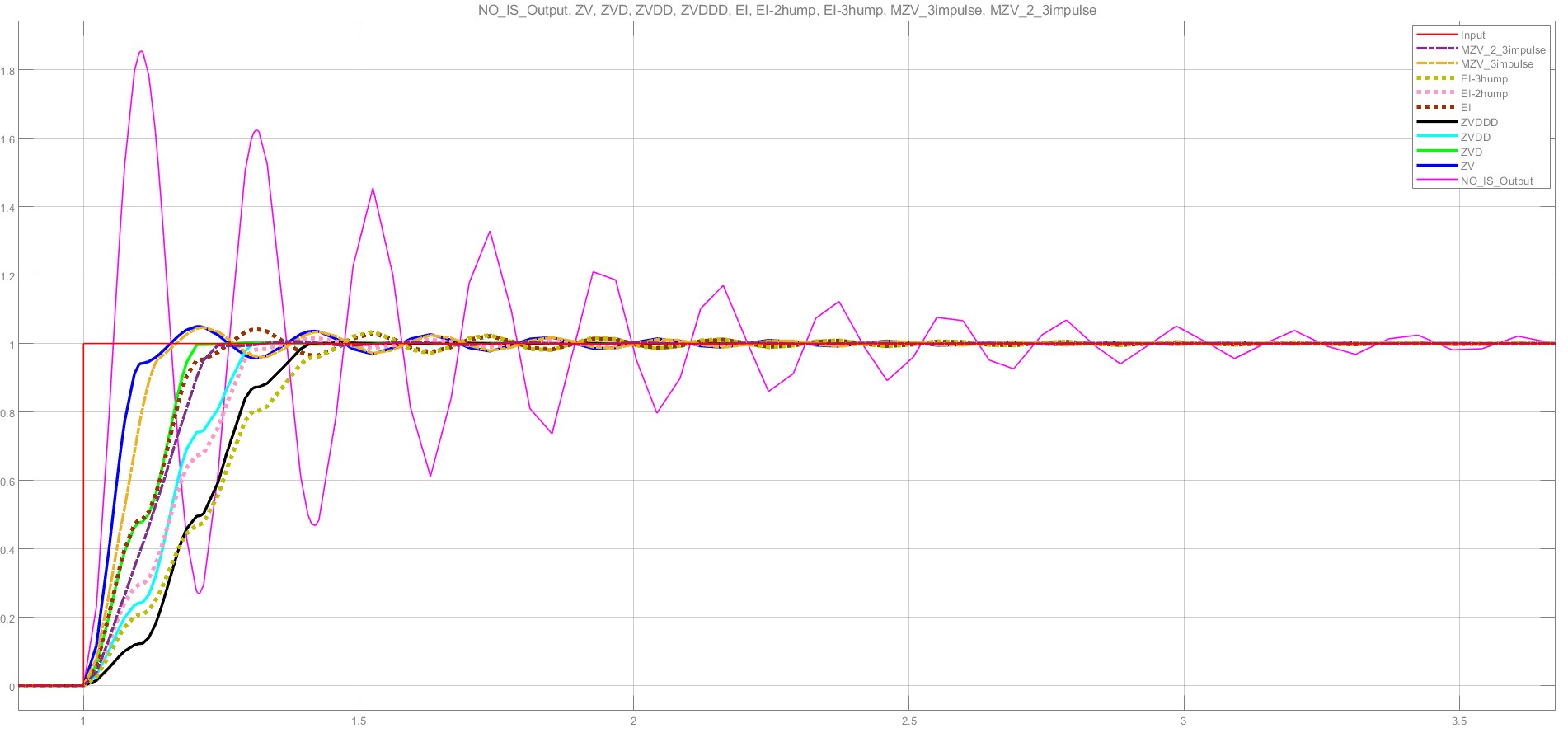
从左往右，调节时间依次增大（ZVD最小，ZV最大）
ZVD	MZV_2_3impulse	ZVDD	EI-2hump	ZVDDD	MZV_3impulse	EI	ZV	EI-3hump

鲁棒性分析

灵敏度分析，用于量化衡量输入整形器的鲁棒性。定义不敏感度为最大允许残余振动范围内包含的频率宽度，不敏感度越大，鲁棒性越好。还可以用于预测可能激发的模态，通过分析在小于、等于和大于系统频率时残余振动，预测输入整形器在不同频率段的效果。

假设系统的频率为30，阻尼比为0.01。

基于频率的灵敏度曲线，假设频率变化区间为（0，500），横坐标为频率，纵坐标为残余振动。从下图中可以看出，当实际频率等于系统频率，残余振动为0，说明系统在没有误差的情况下可以很好的抑制残余振动；当实际频率与系统频率存在误差时，误差越大，残余振动越大。

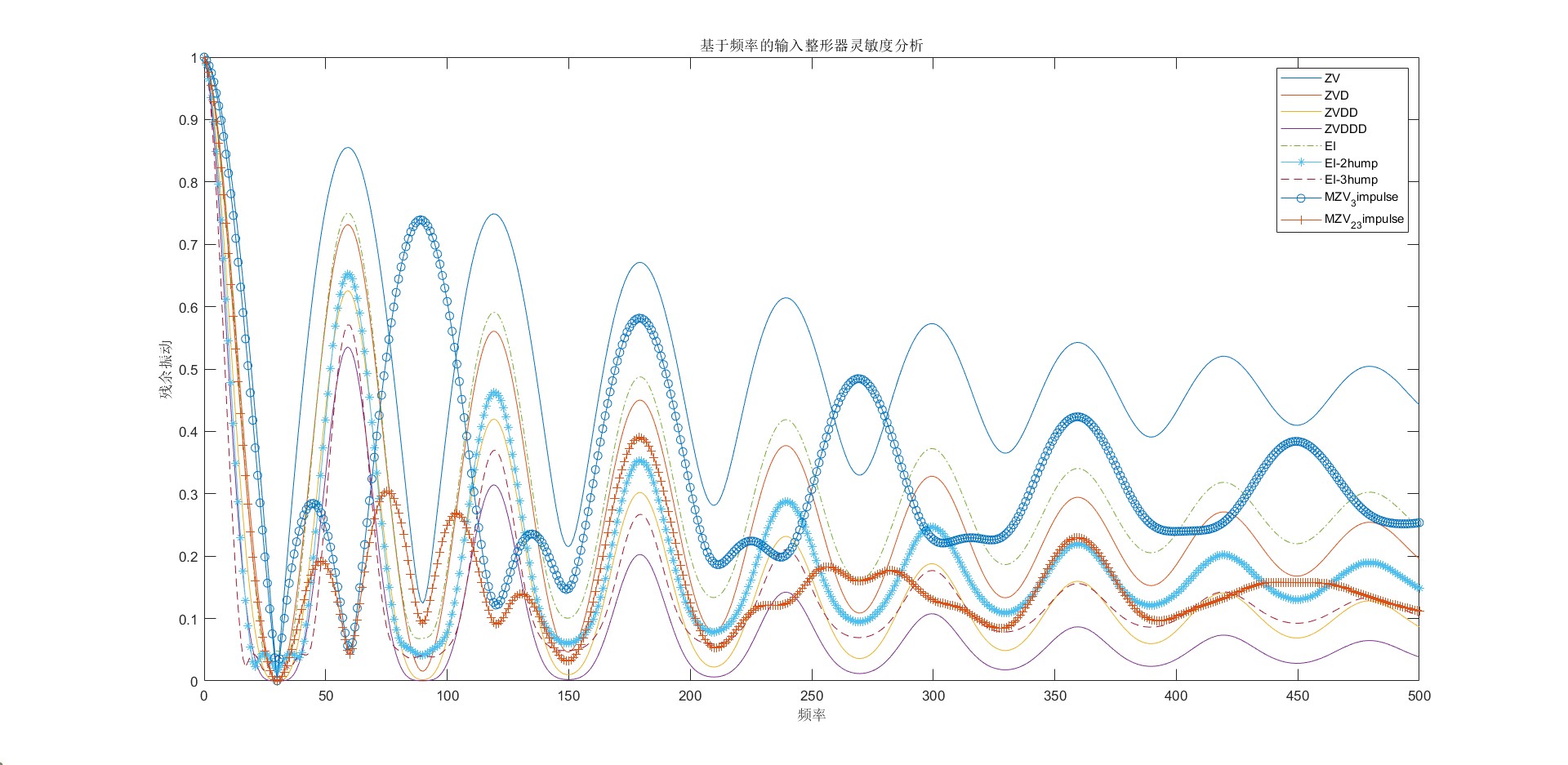
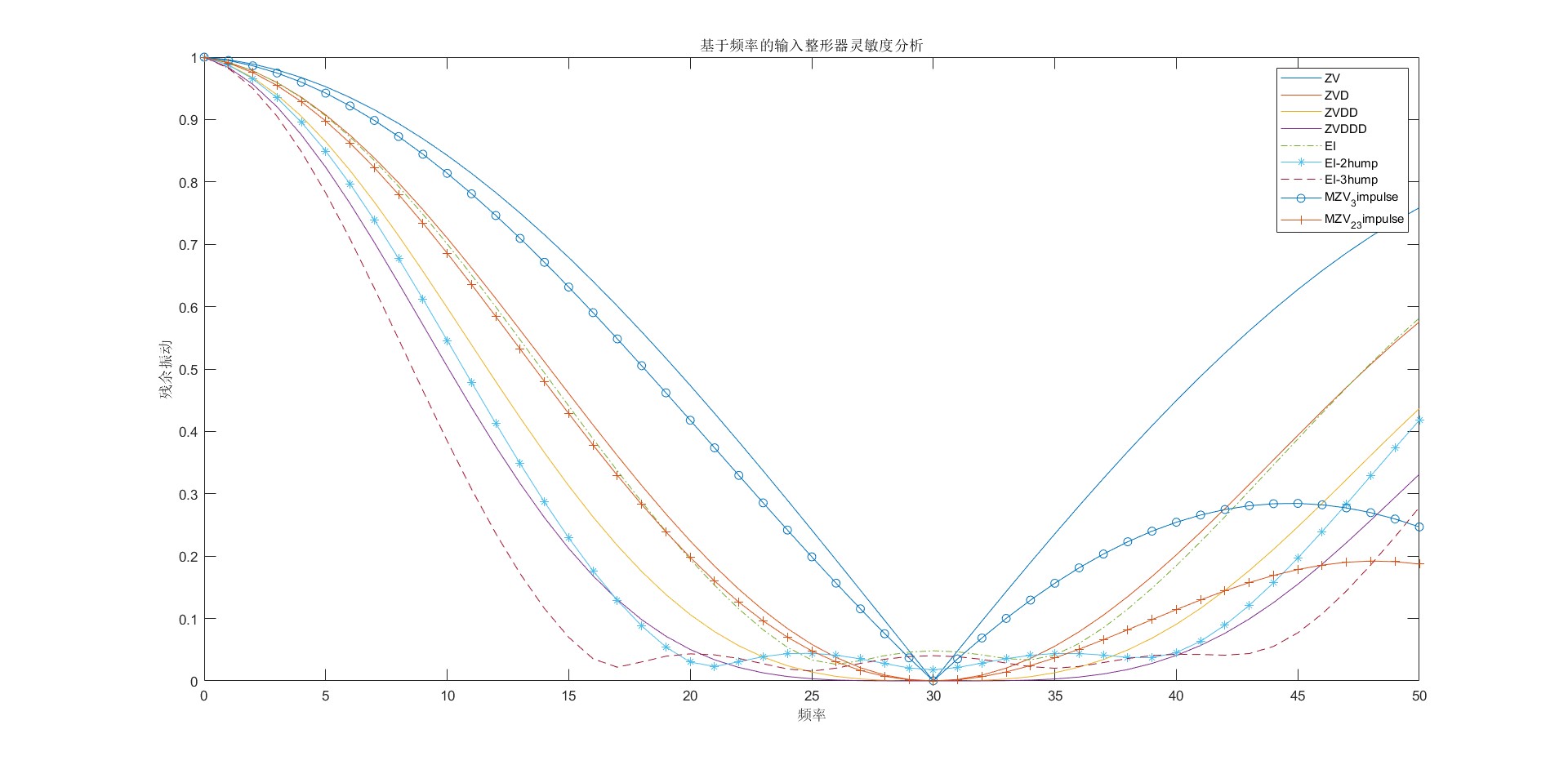
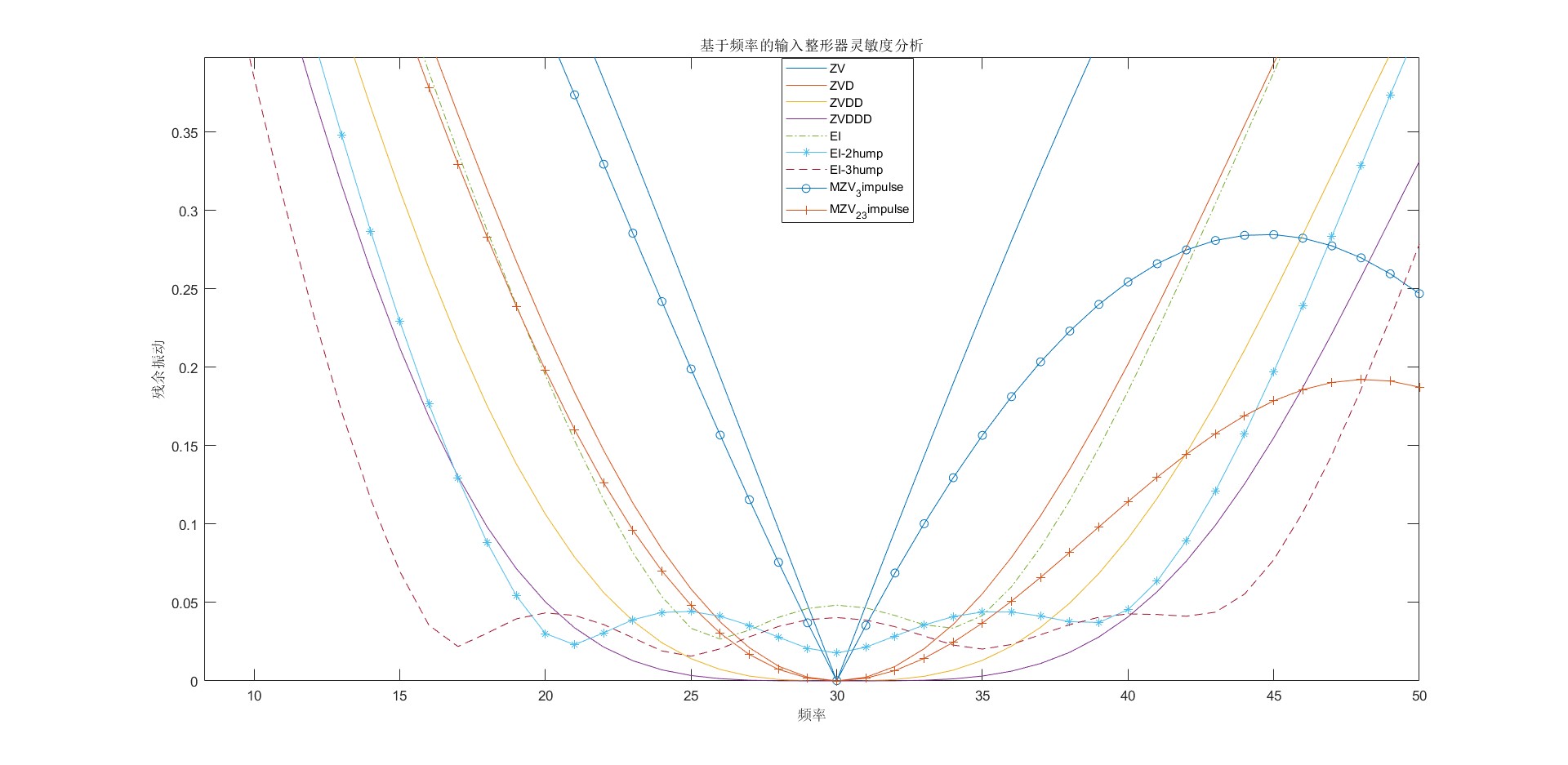
从左往右，不敏感度依次增大（ZV最小，EI-3hump最大）
ZV	MZV_3impulse	ZVD	MZV_2_3impulse	EI	ZVDD	ZVDDD	EI-2hump	EI-3hump

基于阻尼比的灵敏度曲线，假设阻尼比的变化区间为（0.001，0.3），横坐标为阻尼比，纵坐标为残余振动。从下图中可以看出，当实际阻尼比等于系统阻尼比，残余振动为0，说明系统在没有误差的情况下可以很好的抑制残余振动；当实际频率与系统频率存在误差时，误差越大，残余振动越大。

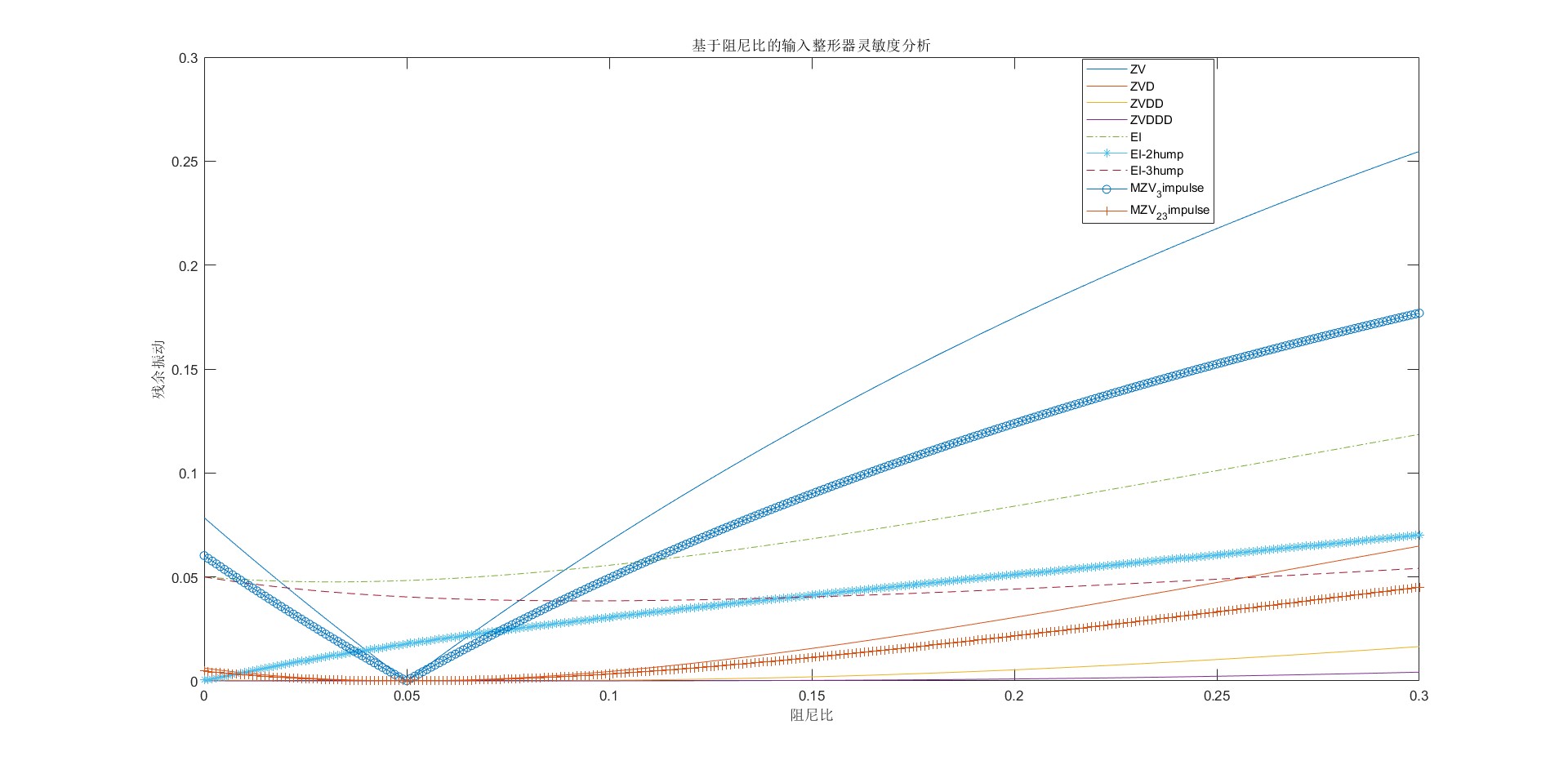
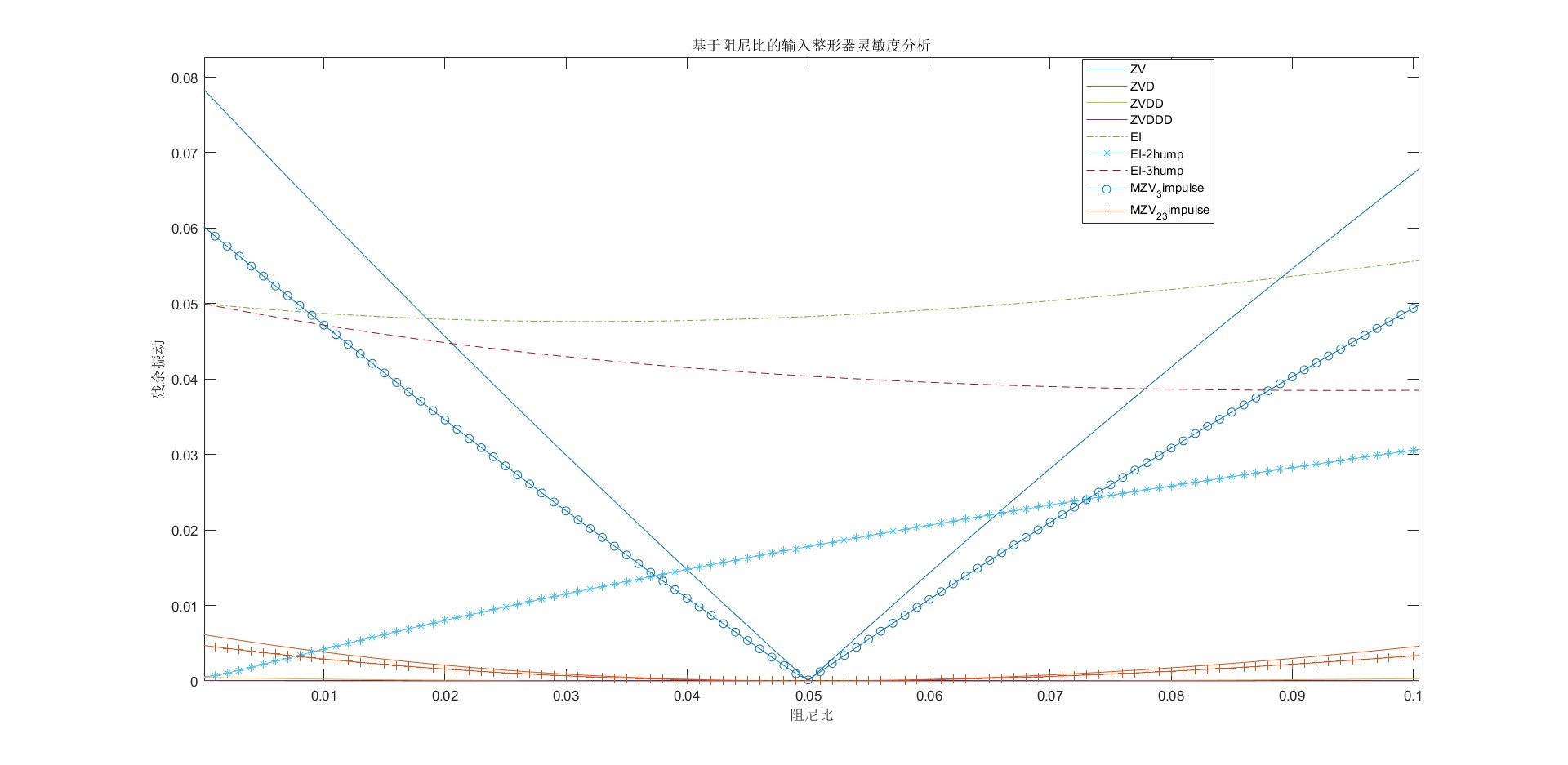
从左往右，不敏感度依次增大（ZV最小，EI-3hump最大）
ZV	MZV_3impulse	EI	EI-2hump	EI-3hump	ZVD	MZV_2_3impulse	ZVDD	ZVDDD

结论：当输入整形器的频率和阻尼比与系统的频率和阻尼比相等，则系统的残余振动可以得到有效抑制；当输入整形器的频率和阻尼比与系统的频率和阻尼比存在一定误差，则系统的残余振动不能得到有效抑制，且误差越大残余振动越大。

优化改进方向

ZV等整形器考虑鲁棒性和响应时间要进行取舍，如果能在线实时获取频率和阻尼比，那么就可以选择响应时间快的整形器，那么如何获取频率和阻尼比成为一个重点，可以建立控制对象的数学模型，根据二阶系统的传递函数间接的估算频率和阻尼比。

Matlab仿真代码

% ****************************************
% 输入整形器分析：时域分析和残余振动分析 
% ****************************************
 
clc;
clear;
close all;
%% 系统传递函数参数
W = 30;      % 系统固有频率
Z = 0.05;    % 系统阻尼比
%% 输入整形器时域分析
% % 测试1：当实际频率 = 系统频率，实际阻尼比 = 系统阻尼比
InputShper_W = 30;
InputShper_Z = 0.05;

% 测试2：当实际频率 > 系统频率，实际阻尼比 = 系统阻尼比
% InputShper_W = 50;
% InputShper_Z = 0.05;

% 测试3：当实际频率 < 系统频率，实际阻尼比 = 系统阻尼比
% InputShper_W = 10;
% InputShper_Z = 0.05;

% 测试4：当实际频率 = 系统频率，实际阻尼比 > 系统阻尼比
% InputShper_W = 30;
% InputShper_Z = 0.1;

% 测试5：当实际频率 = 系统频率，实际阻尼比 < 系统阻尼比
% InputShper_W = 30;
% InputShper_Z = 0.01;

%% 输入整形器参数配置
format long
pi      = pi;
df      = sqrt(1 - InputShper_Z*InputShper_Z);
K       = exp(-(InputShper_Z*pi) / df);
T       = 2*pi / (InputShper_W*df);
V_tol   = 0.05;
%% ZV整形器参数
D = 1 + K;
ZV_A1 = 1 / D;
ZV_A2 = K / D;

ZV_T2 = 1/2 * T;

IS_ZV = [[ZV_A1, ZV_A2];
         [0,     ZV_T2]];
%% ZVD整形器参数
D = 1 + 2*K + K^2;
ZVD_A1 = 1 / D;
ZVD_A2 = 2*K / D;
ZVD_A3 = K^2 / D;

ZVD_T2 = 1/2 * T;
ZVD_T3 = T;

IS_ZVD = [[ZVD_A1, ZVD_A2, ZVD_A3];
          [0,      ZVD_T2, ZVD_T3]];
%% ZVDD整形器参数
D = 1 + 3*K + 3*K^2 + K^3;
ZVDD_A1 = 1 / D;
ZVDD_A2 = 3*K / D;
ZVDD_A3 = 3*K^2 / D;
ZVDD_A4 = K^3 / D;

ZVDD_T2 = 1/2 * T;
ZVDD_T3 = T;
ZVDD_T4 = 3/2 * T;

IS_ZVDD = [[ZVDD_A1, ZVDD_A2, ZVDD_A3, ZVDD_A4];
             [0,       ZVDD_T2, ZVDD_T3, ZVDD_T4]];
%% ZVDDD整形器参数
D = 1 + 4*K + 6*K^2 + 4*K^3 + K^4;
ZVDDD_A1 = 1 / D;
ZVDDD_A2 = 4*K / D;
ZVDDD_A3 = 6*K^2 / D;
ZVDDD_A4 = 4*K^3 / D;
ZVDDD_A5 = K^4 / D;

ZVDDD_T2 = 1/2 * T;
ZVDDD_T3 = T;
ZVDDD_T4 = 3/2 * T;
ZVDDD_T5 = 2 * T;

IS_ZVDDD = [[ZVDDD_A1, ZVDDD_A2, ZVDDD_A3, ZVDDD_A4, ZVDDD_A5];
            [0,        ZVDDD_T2, ZVDDD_T3, ZVDDD_T4, ZVDDD_T5]];
%% EI整形器参数
EI_A1 = (1 + V_tol) / 4;
EI_A2 = (1 - V_tol) / 2;
EI_A3 = (1 + V_tol) / 4;

EI_T2 = 1/2 * T;
EI_T3 = T;

IS_EI = [[EI_A1, EI_A2, EI_A3];
         [0,     EI_T2, EI_T3]];
%% EI_2hump整形器参数
X = (V_tol*V_tol*(sqrt(1-V_tol*V_tol) + 1))^(1/3);
EI_2hump_A1 = (3*X*X + 2*X + 3*V_tol*V_tol) / (16*X);
EI_2hump_A2 = 0.5 - EI_2hump_A1;
EI_2hump_A3 = EI_2hump_A2;
EI_2hump_A4 = EI_2hump_A1;

EI_2hump_T2 = 1/2 * T;
EI_2hump_T3 = T;
EI_2hump_T4 = 3/2 * T;

IS_EI_2hump = [[EI_2hump_A1, EI_2hump_A2, EI_2hump_A3, EI_2hump_A4];
               [0,           EI_2hump_T2, EI_2hump_T3, EI_2hump_T4]];
%% EI_3hump整形器参数
EI_3hump_A1 = (1 + 3*V_tol + 2*sqrt(2*V_tol*(V_tol+1))) / 16;
EI_3hump_A2 = (1 - V_tol) / 4;
EI_3hump_A3 = 1 - 2*(EI_3hump_A1 + EI_3hump_A2);
EI_3hump_A4 = EI_3hump_A2;
EI_3hump_A5 = EI_3hump_A1;

EI_3hump_T2 = 1/2 * T;
EI_3hump_T3 = T;
EI_3hump_T4 = 3/2 * T;
EI_3hump_T5 = 2 * T;

IS_EI_3hump = [[EI_3hump_A1, EI_3hump_A2, EI_3hump_A3, EI_3hump_A4, EI_3hump_A5];
               [0,           EI_3hump_T2, EI_3hump_T3, EI_3hump_T4, EI_3hump_T5]];
%% 3脉冲MZV整形器参数
K = exp(-(2*InputShper_Z*pi) / 3*df);
D = 1 + K + K^2;
MZV_3impulse_A1 = 1 / D;
MZV_3impulse_A2 = K / D;
MZV_3impulse_A3 = K^2 / D;

MZV_3impulse_T2 = 1/3 * T;
MZV_3impulse_T3 = 2/3 * T;

IS_MZV_3impulse = [[MZV_3impulse_A1, MZV_3impulse_A2, MZV_3impulse_A3];
                   [0,               MZV_3impulse_T2, MZV_3impulse_T3]];
%% 6脉冲MZV整形器参数
K = exp(-(InputShper_Z*pi) / 3*df);
D = 1 + K^2 + K^3 + K^4 + K^5 + K^7;
MZV_2_3impulse_A1 = 1 / D;
MZV_2_3impulse_A2 = K^2 / D;
MZV_2_3impulse_A3 = K^3 / D;
MZV_2_3impulse_A4 = K^4 / D;
MZV_2_3impulse_A5 = K^5 / D;
MZV_2_3impulse_A6 = K^7 / D;

MZV_2_3impulse_T2 = 1/3 * T;
MZV_2_3impulse_T3 = 1/2 * T;
MZV_2_3impulse_T4 = 2/3 * T;
MZV_2_3impulse_T5 = 5/6 * T;
MZV_2_3impulse_T6 = 7/6 * T;

IS_MZV_2_3impulse = [[MZV_2_3impulse_A1, MZV_2_3impulse_A2, MZV_2_3impulse_A3, MZV_2_3impulse_A4, MZV_2_3impulse_A5, MZV_2_3impulse_A6];
                     [0,                 MZV_2_3impulse_T2, MZV_2_3impulse_T3, MZV_2_3impulse_T4, MZV_2_3impulse_T5, MZV_2_3impulse_T6]];
%% 残余振动画图
% 基于频率的灵敏度曲线图
% RV_W = 0:1:50;
% RV_Z = InputShper_Z;
% 基于阻尼比的灵敏度曲线图
RV_W = InputShper_W;
RV_Z = 0:0.001:0.3;

RV_ZV             = CalResidualVibration(IS_ZV,             2, RV_W, RV_Z);    
RV_ZVD            = CalResidualVibration(IS_ZVD,            3, RV_W, RV_Z);    
RV_ZVDD           = CalResidualVibration(IS_ZVDD,           4, RV_W, RV_Z);    
RV_ZVDDD          = CalResidualVibration(IS_ZVDDD,          5, RV_W, RV_Z);    
RV_EI             = CalResidualVibration(IS_EI,             3, RV_W, RV_Z);    
RV_EI_2hump       = CalResidualVibration(IS_EI_2hump,       4, RV_W, RV_Z);     
RV_EI_3hump       = CalResidualVibration(IS_EI_3hump,       5, RV_W, RV_Z);   
RV_MZV_3impulse   = CalResidualVibration(IS_MZV_3impulse,   3, RV_W, RV_Z);   
RV_MZV_2_3impulse = CalResidualVibration(IS_MZV_2_3impulse, 6, RV_W, RV_Z);   

figure(1);
% plot( RV_W, RV_ZV, RV_W, RV_ZVD, RV_W, RV_ZVDD, RV_W, RV_ZVDDD, ...
%       RV_W, RV_EI, '-.', RV_W, RV_EI_2hump, '*-',RV_W, RV_EI_3hump, '--', ...
%       RV_W, RV_MZV_3impulse,'O-', RV_W, RV_MZV_2_3impulse,'+-');
% legend('ZV','ZVD','ZVDD','ZVDDD','EI','EI-2hump','EI-3hump','MZV_3impulse','MZV_2_3impulse');
% ylabel('残余振动');
% xlabel('频率');
% title('基于频率的输入整形器灵敏度分析')

plot( RV_Z, RV_ZV, RV_Z, RV_ZVD, RV_Z, RV_ZVDD, RV_Z, RV_ZVDDD, ...
      RV_Z, RV_EI, '-.', RV_Z, RV_EI_2hump, '*-',RV_Z, RV_EI_3hump, '--', ...
      RV_Z, RV_MZV_3impulse,'O-', RV_Z, RV_MZV_2_3impulse,'+-');
legend('ZV','ZVD','ZVDD','ZVDDD','EI','EI-2hump','EI-3hump','MZV_3impulse','MZV_2_3impulse');
ylabel('残余振动');
xlabel('阻尼比');
title('基于阻尼比的输入整形器灵敏度分析')

%% 计算整形器残余振动，输入参数：输入整形器矩阵ARR，整形器脉冲数N，频率W，阻尼比Z
function RV = CalResidualVibration( ARR, N, W, Z)
    C = 0;
    S = 0;
    df = sqrt(1 - Z.*Z);
    Tn = ARR(2,N);
    for i = 1:N
        Ai = ARR(1,i);
        Ti = ARR(2,i);
        C_TEMP = Ai .* exp(Z.*W.*Ti) .* cos(W.*df.*Ti);
        S_TEMP = Ai .* exp(Z.*W.*Ti) .* sin(W.*df.*Ti);
        C = C + C_TEMP;
        S = S + S_TEMP;
    end
    RV = exp(-Z.*W.*Tn).*sqrt(C.*C+S.*S);
end