FMCW雷达系统内的相位噪声
摘要
相位噪声是现代雷达、通信、光谱和计量系统的基本性能参数之一。本文提出了一种适用于FMCW雷达系统的相位噪声理论。导出了一个新的设计方程,用于确定雷达系统中允许的源相位噪声电平的最大界。分析了在传输延迟小于参考振荡器相干时间时,相干混频引起的非线性相位噪声去相关函数;讨论了在传输延迟大于参考振荡器相干时间时,目标响应的频谱展宽。提出了收发链中各子系统的影响,并讨论了一种新的ADC相位噪声模型。介绍了相位噪声建模技术,然后将锁相环频率合成器与低噪声频率合成器进行比较,以演示减少相位噪声边带以改善检测和跟踪性能。利用两个频率合成器对两个毫米波FMCW雷达系统进行了实际测量,以验证所开发的理论。
1 介绍
一个完美的单色正弦波是一种理想化的东西,只能在教科书中找到。所有天然和人造振荡器(无论是光学、电子、声学、原子或任何其他)都表现出相位和频率的不稳定性,统称为相位噪声。这些不稳定性与构成振荡器的材料、振荡器的结构设计以及振荡器中的随机噪声现象有关。本文对调频连续波(FMCW)雷达系统中所用振荡器的相位和频率不稳定性进行了分析。
众所周知,振荡器的短期频率不稳定性,由相位噪声描述,在振荡器频谱中表现为相位调制边带[1]-[3]。线性相位噪声分析[4]-[8]只处理振荡器RF频谱中的低噪声边带分析[4]、[5]、[9]。然而,相位噪声过程也会产生非线性近载波频谱[10]-[13]、相位底噪声以及振荡器信号射频频谱的线宽变宽[12]、[14]、[15]。一个完整的相位噪声分析必须包括射频频谱的所有部分。
振荡器中过多的相位噪声(大于1 rad2)会导致射频频谱的严重失真,表现为中心峰变宽和边带失真。一个设计良好的相干雷达系统应具有远小于1rad2的综合相位噪声。本文将分析信号在倍频下的相位噪声接近这个极限时的情况,并给出传输信号中符合这个极限的允许噪声边带电平的新结果。雷达系统产生的噪声边带响应是目标距离(即时间延迟)的函数[4],即使在雷达中使用低相位噪声主振荡器,由于振荡器中存在频率漂移过程,解调后的返回信号与发射信号失去相干性。因此,设计良好的雷达应在振荡器的相干时间内工作良好[14],[16],以避免解调信号频谱的过度展宽。
FMCW雷达中的相位噪声还没有像雷达系统的其他领域那样得到详细的关注。本文试图填补这一空白。本文特别考虑了对小型低成本雷达的影响,这是目前FMCW雷达系统应用的一个重要领域。从系统方面来看,[5]、[17]-[22]已经从各个方面解决了FMCW雷达中的相位噪声问题。在[5]中,已经介绍了FMCW系统设计的基本原理,包括一些噪声方面。在[17]中讨论了相干积累对相位噪声的影响。文献[18]分析了噪声系数、拐角频率等振荡器噪声参数对相位噪声性能的影响。在[5]和[19]中详细分析了通过接收机混频器泄漏的内部噪声的影响。[20] -[22]中提出了一些后处理相位降噪技术。
本工作的一个重要方面是演示如何通过量化典型FMCW雷达系统各阶段引入的相位噪声来准确地将源相位噪声与中频信号频谱中的相位噪声联系起来,并演示通过使用适当设计的雷达信号源来降低相位噪声。使用这些指导方针,可以返回来确定达到给定动态范围规格所需的源相位噪声电平。
本文的其余部分组织如下。第二节介绍了相位噪声的基本原理,包括本文中使用的符号和定义。第三节介绍了雷达子系统相位噪声模型的发展,提出了FMCW雷达系统的相位噪声建模方法。给出了模数转换器相位抖动消除的新结果。在第四节中,提出了一种新的设计方程的推导,以防止由于发射机中的源相位噪声和/或频率倍增而导致的过度解调相位噪声。第五节演示了建模方法在实际毫米波(MMW)雷达系统中对相位噪声进行精确建模的应用。使用低相位噪声频率合成器实现高动态范围目标识别的好处将通过实际测量来证明。
2 射频频谱中相位噪声的特征
振荡器中的相位噪声最常见的特征是相位波动的谱密度SΦ(f),通常由幂律频率分量组成[23]。另一方面,实际的无线电、雷达和光谱系统,仅举几例,使用振荡器SRF (v0,f)的射频频谱作为其工作频谱,这将是即将讨论的重点。图1a显示了普通振荡器的射频频谱SRF (v0,f),其中v0是测量频谱的中心频率或载波频率,f是载波频率的偏移频率。当SRF (v0,f)中的边带是由相位调制(PM)噪声引起时,它们被称为相位噪声边带,用L(f) = SRF (v0,f)/P(其中P是被测振荡器信号中的总功率)表示,并且具有相对于载波的分贝单位每赫兹(dBc/Hz)。

(a) 一般振荡器的射频频谱

(b)合成雷达信号源的射频频谱,包括噪声基座的参数。
图1 雷达信号源射频频谱示意图。
如图1a所示,频偏f = fα将频谱的相位噪声部分分为两部分,即近载波相位噪声和远载波相位噪声。IEEE标准1139-1999[23]将相位噪声定义为:
 (1)
(1)
本定义中的L(f)为单面量,仅在远载波区域与SRF (v0, f)有关,即对于所有f≥fα,满足:
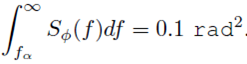 (2)
(2)
在fα下面,SRF (v0, f)与SΦ(f)呈非线性关系。SΦ(f)与归一化双边基带射频频谱![]() )之间的非线性关系如[10]-[12]所示
)之间的非线性关系如[10]-[12]所示
 (3)
(3)
式中![]() 为相位噪声过程Φ(t)的方差,或等价为:
为相位噪声过程Φ(t)的方差,或等价为:
 (4)
(4)
并且假设它是有限的。方程(3)既可以用来建模近载波相位噪声,也可以用来建模远载波相位噪声,尽管在后一种情况下(1)更容易使用。在(3)中,载波被建模为Delta函数:在实践中,SRF (f)具有有限的线宽和定义的线形,这是振荡器中频率噪声过程的函数。这些在[12],[14]中都有涉及。
图1b展示了采用合成信号源的雷达系统所显示的典型目标频谱。相位噪声基座可能源于基于锁相环(PLL)的合成器具有有限环路带宽,或者由于系统中使用的频率乘法链的有限带宽,例如,晶体参考振荡器到更高的频率。在[12],[24],[25]中可以找到关于倍频下噪声基座行为的详细分析,其中给出了噪声边带的测量结果。
式(3)也可以写为:
![]() (5)
(5)
式中,![]() 为中心载波峰的射频频谱密度,
为中心载波峰的射频频谱密度,![]() 为相位噪声基座的射频频谱密度。对于线性相位噪声分析,必须调用低相位噪声条件,
为相位噪声基座的射频频谱密度。对于线性相位噪声分析,必须调用低相位噪声条件, ![]() 。在此条件下(3)化简为:
。在此条件下(3)化简为:
![]() (6)
(6)
图1b中所示的相位噪声基座可以用改进的洛伦兹函数建模如下:
 (7)
(7)
其中![]() 为噪声基座的双面射频频谱密度,Lp为基座的平顶电平(单位为dBrad2/Hz), Wp为噪声基座的3dB宽度,k为滚降阶数,对于微波频率一般在2到4之间。在低相噪条件下,也可由S
为噪声基座的双面射频频谱密度,Lp为基座的平顶电平(单位为dBrad2/Hz), Wp为噪声基座的3dB宽度,k为滚降阶数,对于微波频率一般在2到4之间。在低相噪条件下,也可由S
![]() 计算出
计算出![]() :
:
![]() (8)
(8)
在实践中,这个积分的计算可以对由噪声基座的宽度和滚降的阶数定义的f的有限上限进行。同样,(3)中的有限![]() 假设仅对振荡器信号的有限观测时间Tobs(或测量时间)有效[6],[26]-[28],这实际上相当于为相位噪声谱在1/Tobs处定义一个非零低频截止[27]。当测量次数过大时,相位噪声的闪烁频率和随机游走频率分量会导致被测射频频谱的过度展宽[27]-[30]。
假设仅对振荡器信号的有限观测时间Tobs(或测量时间)有效[6],[26]-[28],这实际上相当于为相位噪声谱在1/Tobs处定义一个非零低频截止[27]。当测量次数过大时,相位噪声的闪烁频率和随机游走频率分量会导致被测射频频谱的过度展宽[27]-[30]。
相位噪声可以等效地定义为振荡器中的时序抖动。标称弧度工作频率为w0=2πv0的信号的RMS时序抖动σt与![]() 的关系为[31],
的关系为[31],
![]() (9)
(9)
相位噪声的时序抖动公式在分析ADC的相位噪声时特别有用。
3 电子子系统中的相位噪声
图2显示了正在考虑的系统的框图,这是一个基本的零差FMCW雷达系统。FMCW信号生成模块使用xN倍频器将FMCW波形的频率倍频至发射频带。接收信号与发射信号混频产生中频信号:发射信号与接收信号的频率差与目标距离成正比[5]。中频信号通过模数转换器(ADC或A/D)进行数字化处理。然后使用复快速傅里叶变换(FFT)处理提取目标的距离、相位、信号强度等信息。在下面的小节中,将讨论这些电子子系统的相位噪声贡献。

图2 一般FMCW雷达系统框图。标记出系统各点处的相位噪声L(f)。
A 频率合成器
间接和直接频率合成器[31]-[33]用于在雷达系统中产生所需的发射波形。流行的例子包括任意波形发生器,锁相环(PLL),直接数字合成器(DDS),以及基于这些的变体。
在基于锁相环的频率合成中,众所周知,在环路滤波器带宽内,参考振荡器的相位噪声占主导地位,而在环路带宽外,电压控制振荡器(VCO)的相位噪声占主导地位[31]。现代基于相频检测器(PFD)的锁相环是通用的,因为它们执行自动相位和频率锁定[31]。然而,对于高动态范围雷达应用,PDF的相位噪声性能可能无法接受[9],导致高水平的带内相位噪声。锁相环合成信号的频谱如图1b所示,其中显示了载波频率周围的噪声基座。
为了降低噪声基座,一种解决方案是减小锁相环的环路带宽。然而,这也降低了通常采用的Type-2 PLL方案[31]中系统的调制带宽。在FMCW雷达的情况下,这是正确合成斜坡波形所需的带宽:环路带宽的过度减少导致锁相环的瞬态响应强劲。因此,调制要求设定了最小可实现环路带宽的限制。锁相环合成器在FMCW雷达系统的背景下已经在[34]-[36]进行了讨论。环路带宽不足也可能导致环路解锁,特别是在扫描结束时需要快速反激时。
偏置锁相环[37]-[39]已成功用于改善相位噪声性能,优于传统锁相环。偏置锁相环在反馈路径中结合混频和分频,以降低环路内的整体倍频因子。由于使用DDS源进行扫频,并且必须对DDS和混频器产生的杂散进行滤波,因此整体结构变得复杂。最先进的DDS合成器比锁相环合成器具有更好的相位噪声,尽管它们更昂贵,并且存在杂散问题[33]。DDS输出通常需要混频到期望的频带,混频器产生自己的杂散。
线性FMCW波形中的寄生非线性,例如,由于压控振荡器(VCO)的非线性调谐曲线,也会导致频谱增宽,但被认为是系统噪声[37],[40]-[42],而不是本质上随机的相位噪声。扫描线性度对FMCW雷达系统性能的影响已经在[37],[40]中得到了解决。在FMCW雷达系统中,通常使用VCO和倍频器的组合来减少VCO非线性调谐特性的影响[43]。
B 倍频器
图3a显示了相位噪声通过倍频器的传播[31]。在倍频过程中,时序抖动保持不变,而相位噪声的RMS增加了N,其中N为倍频因子。倍频器与频率合成器一起使用,以增加传输信号的FM调制指数,以对抗VCO非线性[43]。众所周知,在倍频下,相位噪声边带增加20 log10(N)dB(因此相位信噪比降低20 log10(N) dB)。然而,重要的是要注意,这种增加只发生在小相位噪声近似有效的情况下,即使在频率倍增之后。
对于图1b所示的频谱类型的倍频,已经得出了特殊的结果。在[12]、[24]、[25]中,通过理论分析和实际测量证明,如果![]() < 1,那么在频率乘以N的情况下,Wp保持不变,而Lp则按预期增加20 log10(N)。然而,当
< 1,那么在频率乘以N的情况下,Wp保持不变,而Lp则按预期增加20 log10(N)。然而,当![]() > 1时,载波开始展宽,噪声基座也开始展宽。对于雷达系统来说,这种现象会导致目标响应变宽,从而占用更多的距离bin,这是不希望出现的情况。
> 1时,载波开始展宽,噪声基座也开始展宽。对于雷达系统来说,这种现象会导致目标响应变宽,从而占用更多的距离bin,这是不希望出现的情况。
在倍频过程中,载波的3dB线宽也会增加[14]。一般情况下,雷达信号存在白频率噪声时,线宽增加N^2倍,存在闪烁频率噪声时,线宽增加N倍,存在随机游走频率噪声时,线宽增加N^(2/3)倍[12],[14]。然而,对于短时间延迟,相位噪声过程去相关(稍后解释),导致线宽比预测的更窄[44]。
C 混频器
图3b显示了相位噪声在混频器中的传播[31]。混频器可以用于发射器的上变频(而不是倍频器),也可以用于接收器的下变频。当在发射链中实现时,频率合成器的相位噪声增加到本地振荡器的相位噪声。当在FMCW接收链中实现时,混频器的输入是发送和接收信号,而混频器的输出是中频信号。混频器增加或消除输入信号中的相位噪声:相位噪声的消除发生在两个输入信号是相干的,即它们彼此具有确定的相位关系(或者换句话说,它们来自同一个参考源)。研究表明,在雷达系统中,延时传输信号与自身的混合会导致相位噪声去相关[4],[5],[45],[46]:
![]() (10)
(10)
其中τd为到目标的往返时延。这一关系将在本节后面详细分析。(10)中的一个警告是关于偏置频率变量f的使用。虽然中频处的工作频率可以比Tx处(即发射机)的工作频率低几个数量级,但偏置频率f保持不变。换句话说,式(10)将中频工作频率偏移量f处的相位噪声与发射机工作频率相同偏移量f处的相位噪声联系起来。
由式(10)可知,图2中频阶段的综合(RMS)相位噪声为:
![]() (11)
(11)
一般来说,对于较小的τd,相位噪声消除将会很大。相应地,![]() 会很小。一般来说,对于大的τd,相反的情况是正确的。
会很小。一般来说,对于大的τd,相反的情况是正确的。
参考图3b,如果混频器的两个输入不相关,则综合输出相位噪声为:
![]() (12)
(12)
即使对差频信号也是如此。如果这两个信号的工作频率和相位抖动大致相同,我们有
![]() (13)
(13)
例如,这种情况发生在毫米波(MMW) FMCW雷达中,混频器的两个输入几乎具有相同的工作频率,因此它们的差频是一个非常低频的中频信号。上述结果表明,对于非相干输入,中频信号的综合相位噪声是发射信号的两倍,而时序抖动的关系则更有趣。式(13)可以重新排列为:
![]() (14)
(14)
或者用雷达术语
![]() (15)
(15)
这意味着中频信号中的时序抖动比射频信号中的时序抖动要大得多,因为通常![]() 。这个结果将在下一小节中使用。
。这个结果将在下一小节中使用。
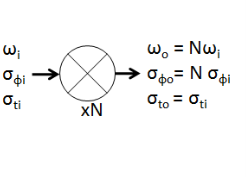
(a)倍频器

(b) 混频器

(c)模数转换器
图3 通过电子子系统的相位噪声传播。
D 模数转换器
在[47]-[52]中讨论了ADC中的相位抖动/噪声问题。如图3c所示,从噪声角度来看,ADC可以被认为是一个时间调制器或时间混频器。扩展混频器中相干相位噪声消除的论点,我们提出,如果输入信号与采样时钟相相干,则采样信号中的抖动是时间去相关的,就像混频器的输入是相位去相关的一样。去相关将取决于被采样信号和时钟信号之间的时间延迟,最重要的是两者的时间抖动有多接近。
如果雷达的发射信号和采样时钟来自相同的参考源,那么它们的时间抖动可以彼此接近。然而,如(15)所述,被采样的中频信号的时间抖动比接收到的射频信号大很多。因此,在这种情况下,时间抖动抵消效果较差。然而,作为指导原则,传输信号的相位抖动通过所使用的频率合成器的传递函数与参考振荡器的相位抖动相关。例如,对于锁相环合成器,锁相环输出端的带内相位抖动等于参考振荡器中的相位抖动,而在环路带宽之外,锁相环输入端和输出端的相位抖动是不相关的。在这种情况下,ADC的采样时钟可用于部分消除带内相位抖动(根据时间延迟),而环路带宽外的频率偏移则无法消除噪声。
对于非相干情况,采样时钟的抖动增加了输入信号的抖动。因此,采样信号中的综合相位噪声为:
![]() (16)
(16)
由于![]() 这一项,中频频率越高的输入信号从采样时钟传递过来的相位噪声越大。[52]在雷达背景下对(16)进行了详细分析。
这一项,中频频率越高的输入信号从采样时钟传递过来的相位噪声越大。[52]在雷达背景下对(16)进行了详细分析。
E 相位噪声去相关
(10)中的相位噪声去相关因子为![]() 。这一因素在解调相位噪声频谱中引入周期性波纹作为τd的函数。(10)中的临界值是fτd= 1/6的频率偏移,其中LIF(f) = LTx(f)。在此频率偏移之外,不会发生进一步的相位噪声消除:实际上LTx(f)和LRx(f)同相增加,因此LIF (f)开始增加。可注意以下几点:
。这一因素在解调相位噪声频谱中引入周期性波纹作为τd的函数。(10)中的临界值是fτd= 1/6的频率偏移,其中LIF(f) = LTx(f)。在此频率偏移之外,不会发生进一步的相位噪声消除:实际上LTx(f)和LRx(f)同相增加,因此LIF (f)开始增加。可注意以下几点:
当频率偏移f ≤1/6τd,相干相位噪声消除发生。
当fτd= 1/4时,LIF (f) = 2LTx(f)。
最后对于f = 1/(2τd), LIF (f) = 4LTx(f)。
最后一点表明,由于相干混频,产生的相位噪声可能比发射机的相位噪声大6dB。
上述讨论适用于延迟次数小于振荡器相干时间的情况[14],[16]。如前所述,对于过大的测量时间(或在雷达系统的情况下在很长的距离上进行测量),振荡器中的频率噪声过程会导致被测射频频谱的过度展宽[27]-[30]。[28],[44]分析了频谱的载波部分和边带部分之间的功率如何随延迟时间τd的变化而变化。
作为最后的评论,如果在雷达系统中使用非相干混频,在任何距离都不会发生相位噪声的消除。实际上,中频相位噪声只是发射机相位噪声的两倍,并且不会观察到相干波纹。与相干雷达相比,目标响应的线宽也更大。
F 系统噪底
图2显示了系统中影响整个系统底噪性能的两个放大器[5],[17]。在接收机中加入一个低噪声放大器(LNA)作为第一级,可以最大限度地减少系统的热噪声。然而,使用LNA有两个主要缺点。首先,靠近雷达的目标会产生较大的反射信号。LNA进一步放大这些信号,导致混频器阶段比没有LNA时更早饱和。其次,从发射机到接收机的直接泄漏信号被LNA进一步放大。在某些情况下,该相位噪声泄漏信号可以支配接收机的底噪,从而使LNA的热降噪作用被抵消。发射机中的功率放大器(PA)使雷达能够在更远的范围内检测,但也增加了泄漏信号。功率放大器还可以通过添加独立的噪声分量(不会被混频器抵消)来扭曲噪声频谱,也可以通过调幅噪声到调频噪声的转换,当需要高水平的抵消时,这可能会很重要。
因此,需要进行完整的噪声分析,将热噪底与泄漏相噪底进行比较。相位噪声泄漏的另一个途径是通过接收机的混频器级。这些噪声成分的详细分析可以在[4],[5]中找到。来自功率放大器的额外噪声可以通过从功率放大器后的混频器本振处理,或者在一些单稳态FMCW配置中采用额外的泄漏噪声消除级来处理。
作为最后的评论,应该注意的是,泄漏信号解调到零,或几乎零的工作频率。因此,对于图2所示的单通道系统,负相位噪声边带将折叠并添加到正边带。因此,平均底噪将提高3dB。然而,在使用I/Q解调的系统中,这不会是一个问题。
4 底座高度Lp的最大边界
讨论了 ![]() > 1对典型雷达信号源的影响后,有必要进一步分析这种情况。图1b显示了以载波频率v0为中心的射频频谱中的相位噪声基座,以及中心载波峰值。相位噪声基座的双面基带模型是(7)中描述的广义洛伦兹函数,但为了方便起见,这里重复,
> 1对典型雷达信号源的影响后,有必要进一步分析这种情况。图1b显示了以载波频率v0为中心的射频频谱中的相位噪声基座,以及中心载波峰值。相位噪声基座的双面基带模型是(7)中描述的广义洛伦兹函数,但为了方便起见,这里重复,
 (17)
(17)
其中Lp和Wp如图1b所示,k为基座滚降的阶数。
现在我们将推导给定Wp下Lp的最大界,以满足条件![]() <1对于k≥2。注意,噪声基座显然不包括中心载波峰值和相位底噪。若
<1对于k≥2。注意,噪声基座显然不包括中心载波峰值和相位底噪。若![]() < 1,则
< 1,则![]() 近似等于基座噪声功率的均方根值,可计算为:
近似等于基座噪声功率的均方根值,可计算为:
![]() (18)
(18)
对不同k值下的上述积分进行求解,结果如表1所示。第二列表明,在较大k的极限下,积分收敛到![]() = WpLp。第三列表明,对于每个k, Lp作为Wp的函数的最大界。
= WpLp。第三列表明,对于每个k, Lp作为Wp的函数的最大界。
表1(第四列)还显示了Wp/2=100 kHz时计算的Lp值(该Wp值将在下一节的图中使用)。请注意,要从以dB-rad2/Hz为单位的Lp值中减去3dB,以计算以dBc/Hz为单位的Lp的单边带电平:后者将是在以载波频率v0为中心的频谱分析仪上测量的Lp的代表性值。
表1给出了一个有趣的结果,即Lp上的最大界不随k的变化而发生显著变化。积分的最大值出现在k = 2处,给出了Lp上最紧的界。因此,为了保证![]() <1,我们需要,
<1,我们需要,
![]() (19)
(19)
(19)的美妙之处在于,这个结果不依赖于雷达的实际工作频率或倍频系数。雷达的发射机只需要符合这个限制作为一个可接受的雷达信号源的最低限度。如果Lp和Wp更低,雷达信号源保持自身相干(或自相干)的范围要比Lp和Wp更大的雷达信号源大得多。这里开发的模型与[12]中的测量结果非常吻合,也恰好是9.5 GHz。
Wp的变化会直接影响到Lp的界。例如,如果10 kHz的噪声带宽足以满足发射机中使用的锁相环,则Wp = 20 kHz,最大允许Lp = -48 dBc/Hz以确保![]() <1。因此,通过降低Wp, Lp的约束被放宽了。最后,我们强调Lp上的边界已经以dBc/Hz的单位表示(即归一化到积分带宽),并且应该这样使用。
<1。因此,通过降低Wp, Lp的约束被放宽了。最后,我们强调Lp上的边界已经以dBc/Hz的单位表示(即归一化到积分带宽),并且应该这样使用。
表1 不同k值的最大允许Lp。

5 相位噪声建模在毫米波FMCW雷达系统中的应用
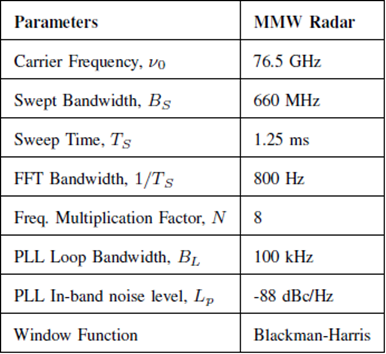
相位噪声建模方法应用于具有如图2所示子系统的商用毫米波FMCW雷达系统。雷达系统参数如表二所示。首先,利用基于锁相环的雷达信号源测量三面角反射器的目标响应。相位噪声边带将在此测量中可见。接下来,将使用低相位噪声源进行相同的测量,以演示性能改进。
表2 正在研究的FMCW雷达参数。
A 基于锁相环系统的相位噪声建模
用于测量的雷达最初采用PLL/VCO方案产生X波段信号,倍频到76.5 GHz。图4显示了非扫频载波信号的频谱分析仪显示。由于扫频带宽与载波相比较小,因此扫频信号的相位噪声水平预期相同。相位噪声边带是可见的:例如,在100 kHz时,相位噪声约为-88 dBc/Hz。
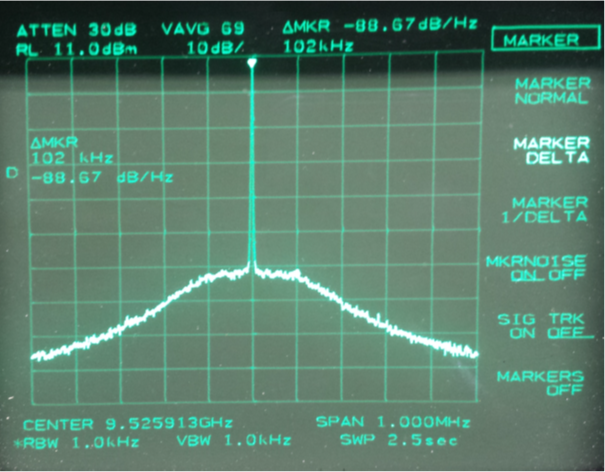
图4 X波段锁相环合成振荡器的实测射频频谱。
进行了76.5 GHz传输信号的频谱测量 (但不包括在这里),证实噪声基座的宽度没有变化,基座高度确实增加了20 logN = 18 dB。这符合上一节提出的理论:噪声基座高度Lp = -88 dBc/Hz远小于表1建议的最大边界。图5显示了考虑使用(10)进行相位噪声去相关的影响,在不同目标距离内仿真的最终单边带目标响应。这种仿真模型对于预测目标的预期响应,分析雷达系统的相位噪声性能具有重要的意义。在相干波纹的峰值处,仿真的目标响应比预期的高6 dB。临界频偏fcrit = 1/6τd(转换为距离bin值)绘制为垂直虚线:可以看出,超过此点后,相位噪声边带增加到发射机综合相位噪声电平之外的6dB,并且除了波纹的波谷之外没有进一步的相位噪声消除。
在150 m处仿真目标响应的峰值相位噪声电平为-45 dBc,在750 m处仿真目标响应的峰值相位噪声电平为-33 dBc。这些值将与下一小节的测量结果进行比较。由于射频工作频率(76.5 GHz)和中频(高达7 MHz)之间的差异很大,因此ADC抖动的计算影响很小,对测量的影响也很小。

图5 不同距离的目标响应(单边带)图。相干相位噪声消除可以改善(降低)垂直虚线左侧区域的相位噪声。
B 基于锁相环的雷达测量结果
图6显示了分别位于173 m和770 m的两个角反射器目标的测量结果。测量使用Navtech雷达有限公司开发的CTS雷达系统完成,参数见表2。这一数据也出现在[9]中,但进行了新的分析。可见,热噪声叠加在相位噪声边带上,因此应取平均噪声级作为相位噪声的代表值。两个双箭头的下端已被放置,以指示预期的信号到相位噪声水平。
从图5可以看出,理论模型与实验结果相吻合。在173m处测量到的目标响应确实具有-45 dBc左右的平均相位噪声水平,而在770 m处测量到的目标响应具有-33 dBc左右的平均相位噪声水平。

图6 173米和770米目标。距离bin每个25厘米。
C 基于锁相环的雷达测量的讨论
100khz的调制环路带宽使锁相环具有200khz的大噪声带宽(或噪声基座宽度)。结果是图6中的两个目标都有大的肩状侧带叠加在它们上面。这种现象给噪声本底升高区域内目标的检测和跟踪带来了严重的困难:所有目标的检测都被降低,小目标可能在该噪声本底中消失。
为了更好地理解相位噪声的伪影,我们使用了具有17.5 cm距离bin的高功率雷达。图7为770 m角反射器的实测目标响应。平均处理以减少显示中噪声成分的方差。在这张图中,连贯的边带结构与其他小目标(较近距离的草和较远距离的树)一起更加明显。相干波纹可以与图5右上方插入的波纹进行比较。可以注意到,测量的边带电平现在是-30 dBc而不是-33 dBc,因为这种特殊的雷达使用更严格的环路带宽,导致带内相位噪声增加。然而,这并不影响相干波纹的宽度。
值得注意的是,图7中的相干纹波只有在频率合成器中减轻系统噪声后才可见[32]。系统噪声的存在可以涂抹边带结构,也会引起噪声底升高。我们将不再详细讨论系统噪声。
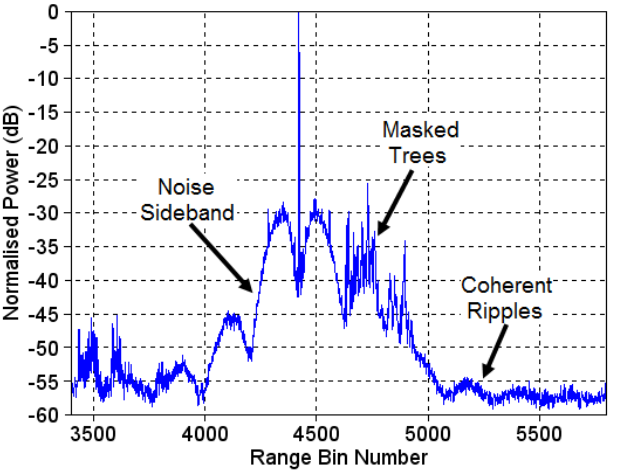
图7 采用基于锁相环源的更高功率雷达产生的770米目标响应。
D 改进的相位噪声设计
为了降低相位噪声的边带,我们设计了一个低相位噪声频率合成器。频谱分析仪显示合成器的输出如图8所示。与图4的比较表明,对于一个紧凑、低成本的源,新的合成器确实具有非常低的相位噪声。在100 kHz偏移处,测量到的相位噪声为-111.8 dBc/Hz,比锁相环源至少好23 dB(因为该测量接近频谱分析仪的噪声底):如下所示,实际改进大于30 dB。图9给出了两种源的建模的相位噪声谱的比较。相位噪声边带和相位底噪有了很大的改善。新型低噪声合成器中的去相关效果可以使用类似于图5的图来计算。

图8 低相位噪声源的测量射频频谱
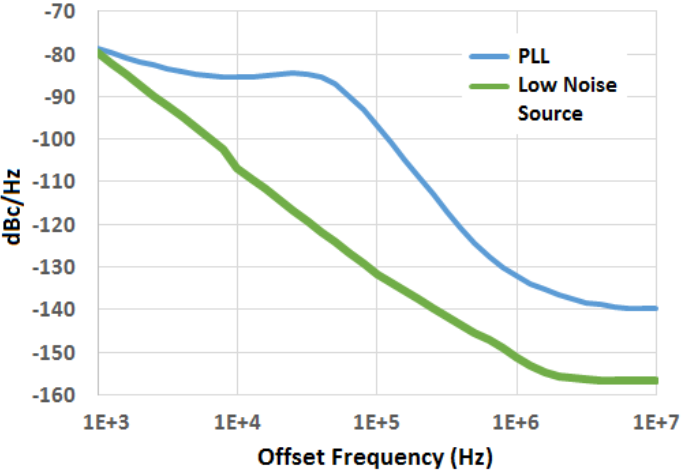
图9 锁相环源和低噪声源在9.5 GHz处的相位噪声建模。
图10显示了与图7相同的场景,使用采用新型低噪声频率合成器的更高功率雷达系统。可以看到30 dB左右的相位噪声边带得到了显著改善,显著提高了场景中的清晰度。目标前的草地和目标后的树木现在都清晰可见。此外,在角落反射器后面的一个树篱现在已经显示出来,在图7中完全隐藏。因此,现在可以精确地探测到这个大目标附近的任何小目标。这种改进的潜在应用是在周边安全系统中,入侵者就在大型建筑物旁边行走:由于建筑物周围的大雷达响应的相位噪声边带的传播,传统的雷达传感器将无法捕捉到入侵者。然而,一种基于低相位噪声技术的改进雷达系统确实能够探测到入侵者并发出警报。
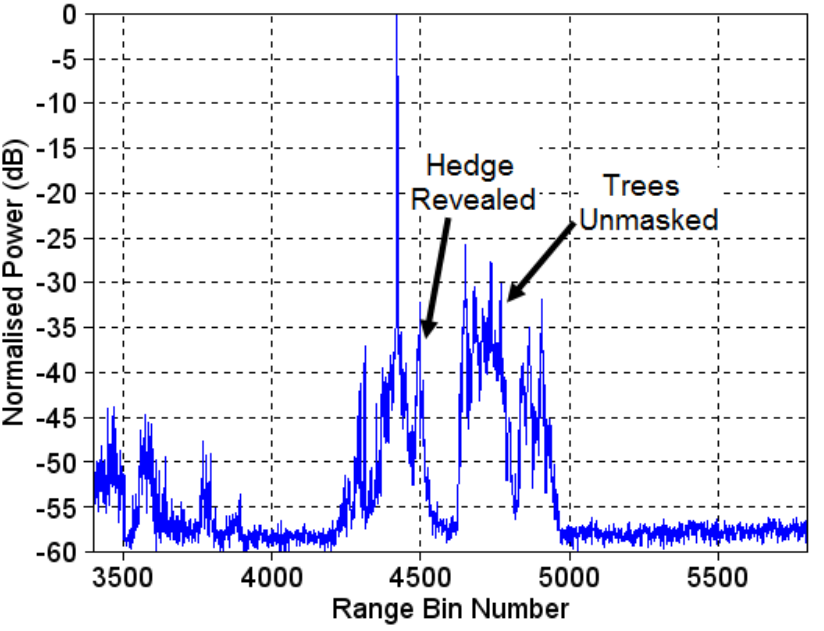
图10 高功率低相位噪声源雷达显示的770 m目标。相位噪声边带已基本消除。
6 结论
FMCW雷达系统中导致目标响应谱增宽的原因有很多,包括相位噪声、透镜未聚焦、VCO调谐曲线产生的寄生非线性等内部因素,以及交叉解调雷达干扰信号[53]、环境降水、目标分布等外部因素。本文主要研究了相位噪声对雷达目标响应边带频谱展宽的影响。描述了一种完整的相位噪声分析方法,用于建模完整雷达系统各阶段的相位噪声。提出了新的ADC相位噪声模型和相位噪声基座模型,并将其应用于雷达系统的相位噪声建模。讨论了影响解调信号线宽的因素。所提出的测量结果与已发展的理论非常吻合。最后,利用低相位噪声频率合成器将相位噪声边带降低了30 dB,显著提高了雷达的探测和跟踪性能。



























 1292
1292

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










