用循环神经网络预测股价

循环神经网络可以用来对时间序列进行预测，之前我们在介绍循环神经网络RNN,LSTM和GRU的时候都用到了正弦函数预测的例子，其实这个例子就是一个时间序列。而在众多的时间序列例子中，最普遍的就是股价的预测了，股价序列是一种很明显的时间序列，价格随时间变化，每天都有一个收盘价。本文就打算使用简单循环神经网络RNN和长短期记忆网络LSTM来对股价进行一下预测。

我们打算利用前N天的股票收盘价来预测下一日的股票收盘价，所以首先需要获取股票数据，这里我使用akshare接口来获取数据，个人觉得比tushare好用。

虽然变量名取了df_hs300，但我没有用沪深300指数，我选择了浙大网新这个股票，毕竟是自己学校下面的企业，支持一下：）

df_hs300 = ak.stock_zh_a_hist(symbol="600797", period="daily", start_date="20210101", end_date=datetime.datetime.today().strftime("%Y%m%d"), adjust="")

获取了从2021年1月1日到当前的股票数据，我们可以输出这个数据看一下：

而我这里只需要收盘价以及日期两个字段，并把收盘价进行归一化处理，更便于训练：

close_list = df_hs300['收盘'].values
date_list = df_hs300['日期'].values
close_list_norm=[price/max(close_list) for price in close_list]

可以打印出来看一下

%matplotlib inline
import matplotlib.pyplot as plt

plt.plot(close_list_norm)
plt.title('hs_300')
plt.xlabel('date')
plt.ylabel('colse price')
plt.show()

下面，根据这个数据集定义一个Dataset和DataLoader，我选择用前10天的收盘价来预测下一个交易日的收盘价，所以时间步选择了10，并用前700个数据作为训练数据集。

from torch.utils.data import Dataset, DataLoader  

class StockDataset(Dataset):
    def __init__(self, data_list, time_step = 10, transform=None):
        self.data = data_list
        self.features = []
        self.targets = []
        for i in range(len(self.data)-time_step):
            feature = [x for x in self.data[i:i+time_step]]
            y = self.data[i+time_step]
            #feature = torch.Tensor(feature)
            #feature = feature.unsqueeze(1)
            y = torch.tensor(y)  
            y = y.reshape(-1)
            self.features.append(feature)
            self.targets.append(y)
        self.features = torch.tensor(self.features)
        self.features = self.features.reshape(-1, time_step, 1)
        
    def __len__(self):
        return len(self.features)
    
    def __getitem__(self, idx):
        return self.features[idx], self.targets[idx]
        
transform = transforms.Compose([transforms.ToTensor()])
dataset = StockDataset(close_list_norm[:700], time_step=10, transform=transform)
dataloader = torch.utils.data.DataLoader(dataset=dataset, batch_size=1, shuffle=True)

我先用简单循环神经网络来训练一下该数据集，下面定义了这个RNN模型以及一些初始化参数：

time_step = 10
batch_size = 1
#设计网络(单隐藏层Rnn)
input_size,hidden_size,output_size=1,20,1
#Rnn初始隐藏单元hidden_prev初始化
hidden_prev=torch.zeros(1,batch_size,hidden_size).cuda()
class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.rnn=nn.RNN(
            input_size=input_size,    #输入特征维度,当前特征为股价，维度为1
            hidden_size=hidden_size,  #隐藏层神经元个数，或者也叫输出的维度
            num_layers=1,
            batch_first=True
        )
        self.linear=nn.Linear(hidden_size,output_size)

    def forward(self,X,hidden_prev):
        out,ht=self.rnn(X,hidden_prev)

        batch_size, seq,  hidden_size = out.shape

        out = self.linear(out[:, -1, :])  # 其实就是取出输出的序列长度中的最后一个去进行线性运算，得到输出
        return out

定义一个训练方法：

model=Net()
model=model.cuda()
criterion=nn.MSELoss()
learning_rate,epochs=0.01,500
optimizer=torch.optim.Adam(model.parameters(),lr=learning_rate)
for epoch in range(epochs):
    losses = []
    for X,y in dataloader:
        X = X.cuda()
        y = y.cuda()
        y=y.to(torch.float32)
        X=X.to(torch.float32)
        #print("X.shape: ",X.shape)
        #print("y.shape: ",y.shape)
        optimizer.zero_grad()
        yy=model(X,hidden_prev)
        yy=yy.cuda()
        #print("yy.shape: ",yy.shape)
        #print(yy)
        #print(y)
        loss = criterion(y, yy)
        model.zero_grad()
        loss.backward()
        optimizer.step()
        losses.append(loss.item())
    epoch_loss=sum(losses)/len(losses)
    if epoch%50==0:   #保留验证集损失最小的模型参数
        print("epoch:{},loss:{:.8f}".format(epoch+1,epoch_loss))
torch.save(model, "model2.pt")
# 输出：
epoch:1,loss:0.00685027
epoch:51,loss:0.00065118
epoch:101,loss:0.00120512
epoch:151,loss:0.00215360
epoch:201,loss:0.00149827
epoch:251,loss:0.00173493
epoch:301,loss:0.00188238
epoch:351,loss:0.00167589
epoch:401,loss:0.00165730
epoch:451,loss:0.00160637

我们把训练后的模型在验证数据集上测试一下，首先定义验证数据集，训练数据集选择所有数据的前700个数据，验证数据集就选择700个以后的数据作为验证数据集。

transform = transforms.Compose([transforms.ToTensor()])
val_dataset = StockDataset(close_list_norm[700:], time_step=10, transform=transform)
val_dataloader = torch.utils.data.DataLoader(dataset=val_dataset, batch_size=1, shuffle=False)

定义验证方法

model = torch.load('model2.pt')

Val_y,Val_predict=[],[]
#将归一化后的数据还原
Val_max_price=max(close_list) 
for X,y in val_dataloader:
    with torch.no_grad():
        X = X.cuda()
        y=y.to(torch.float32)
        X=X.to(torch.float32)
        print("X: ",X)
        predict=model(X,hidden_prev)
        y=y.cpu()
        predict=predict.cpu()
        print("y: ",y)
        print("predict: ",predict)
        # 把股价还原为归一化之前的股价
        Val_y.append(y[0][0]*Val_max_price) 
        Val_predict.append(predict[0][0]*Val_max_price)

fig=plt.figure(figsize=(8,5),dpi=80)
# 红色表示真实值，绿色表示预测值
plt.plot(Val_y,linestyle='--',color='r')
plt.plot(Val_predict,color='g')
plt.title('stock price')
plt.xlabel('time')
plt.ylabel('price')
plt.show()

我们可以看到，总体趋势是一致的，但是真实值和预测值之间的差距确实有点大，那么我们接下来看一下LSTM网络的模型表现如何：

class Net_LSTM(nn.Module):
    def __init__(self):
        super(Net_LSTM,self).__init__()
        self.lstm=nn.LSTM(
            input_size=input_size,    #输入特征维度,当前特征为股价，维度为1
            hidden_size=hidden_size,  #隐藏层神经元个数，或者也叫输出的维度
            num_layers=1,
            batch_first=True
        )
        self.linear=nn.Linear(hidden_size,output_size)

    def forward(self,X):
        out,ht=self.lstm(X)      
        batch_size, seq,  hidden_size = out.shape
        out = self.linear(out[:, -1, :])  # 其实就是取出输出的序列长度中的最后一个去进行线性运算，得到输出
        return out

因为训练和验证的函数和用RNN训练和验证的函数基本是一致的，我就不赘述了，我们来看看利用LSTM进行训练后的模型，在验证集上的表现如何：

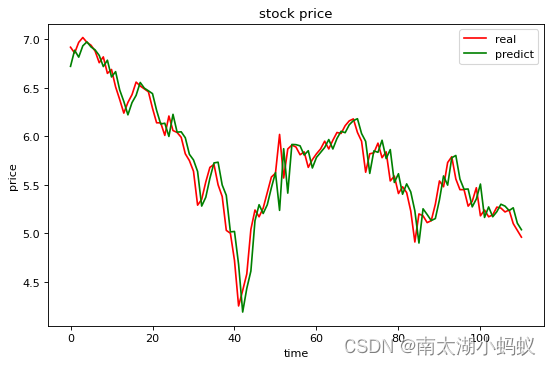
可以看到，这个效果比起用简单循环神经网络RNN好上了很多，可见LSTM的效果确实比简单RNN要提高了不少。这只是一个例子而已，不建议根据这个结果去进行投资，因为预测结果在细节上和原始数据还是有不少差别的，而且只能验证下一个交易日的情况，如果预测时间稍微拉长，效果就会急剧下降，并当前预测都是在前期的数据集的基础上进行预测，如果有突发事件的发生，模型是捕捉不到的。