基于LQR的二自由度云台控制与仿真

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

目录

前言

一、系统概述

二、LQR控制器设计与仿真

1.LQR基本原理

2.LQR控制器设计

3. 状态观测器设计

 三、仿真结果

附录  求解反馈增益矩阵K的matlab程序

总结

---

前言

云台在智能安防、自动攻击火炮以及人机交互领域扮演者重要的角色，例如将视觉系统和火炮攻击系统整合于多自由度云台上，利用计算机视觉技术进行敌对目标快速锁定，以实现对目标的跟踪和打击。

       目前，经典控制理论的PID控制，在系统的控制精度、抗干扰和多目标控制性能的需求下已经显得乏力。本课程作业从二自由度的云台的控制角度出发，结合现代控制理论技术，进行基于LQR输出反馈控制器的设计，以满足云台控制系统在快速性、稳定性和鲁棒性上的需求。

一、系统概述

1.系统建模（直接使用作者系统辨识后得到的云台模型的传递函数） 由系统辨识和高阶系统降阶方法得到云台模型的传递函数：

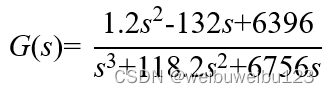
由simulink绘制系统的开环模拟结构图，所述的结构图如图所示

 对应的状态方程空间表达式：

 

云台模型的开环Bode图，以及单位闭环的单位阶跃响应如图所示：

开环系统Bode图与闭环系统单位阶跃响应 

        由上图可知，云台系统的调节时间约为3.9s，截止频率为0.947rad/s,幅值裕度为32dB，系统具有一定的幅值裕度，但是系统的响应速度慢，不满足实际的应用需求，原系统的快速性有待提高，故而设计的控制器应该保证系统在有一定的稳定裕度的情形下，提升系统的响应速度。

二、LQR控制器设计与仿真

1.LQR基本原理

标准的LQR控制系统的设计如图所示：

标准的LQR控制系统结构图

      其中G(s)为被控对象，K为状态反馈矩阵， 为通过状态估计得到估计状态，u为被控对象控制信号，z表示控制器的控制输出，y为能够测量得到的输出信号。LQR 控制率为：  ，其主要目标是寻求合适的控制信号u, t ∈(0,∞) 使得所示目标函数最小。

 

 可进一步改写为：

      上述指标函数中，Q为半正定权矩阵，R为正的权系数。控制输出z一般可根据实际系统的控制要求来选定，不同的控制输出z 对应不同的控制方案，且当控制输出z确定后，相应的矩阵Q和R的值也确定下来。

       确定权矩阵Q和权系数R后，求解Riccati方程即可得到最优状态反馈矩阵K，Riccatic方程得到的状态反馈矩阵

 

         通常情况下，在设计 LQR 控制器时只考虑零输入时的情况。在云台控制系统中，可考虑加入一个比例积分环节，以便于控制系统实现零误差跟踪。加内模控制的LQR状态反馈控制器的闭环结构框图如图，K4为内模状态控制系数， 为云台实时输出的角度值。

 LQR状态反馈控制器的闭环结构框图

2.LQR控制器设计

        LQR 控制器设计，需要得到系统的所有状态值，但在实际系统中，只能通过绝对值编码器测量角度信号，而系统为三阶模型有三个状态变量，因此必须设计状态观测器。线性系统理论指出，基于 LQR 输出反馈控制设计包含状态反馈设计和状态观测器设计，而两者又是相互独立的，故可以分开独立设计。

1）状态反馈设计

       在本次设计采用内模加状态反馈的方法设计控制器，内模状态为x4 ，控制率为u(t) = −Kx(t) 。加内模后系统的simulink模拟结构图如图所示。加入内模状态后的系统状态空间表达式如式所示：

加入内膜控制和LQR控制的系统结构图

令

选择

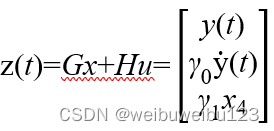
      这样就可以让被测输出 y(t) 和它的导数 y(t) 都很小，同时内模积分器的输出也得到了限幅。让系统的稳态性能和动态性能都得到保证。则

 考虑目标函数J，则有：

       求解Riccati方程即可得到最优状态反馈矩阵K，得到的状态反馈矩阵。

所设计的状态反馈控制器中，其中三个参数（γ0，γ1，ρ ）为系统的控制权系数，选取不同的控制权重系数后，再求解对应的黎卡提方程就可以得到对应的状态反馈矩阵K，闭环极点P。下面是关于LQR三个控制权重系数分析：

       a.要使代价函数较小，而又不使控制作用减弱，参数ρ应越小越好；

       b. γ0 表征系统状态速度  ，期望系统的状态速度越快越好，应该越小越好；

      c. γ1 与表征系统的累积误差e有关，系统的累积误差越小越好，故越大越好。

分析参数ρ的影响：

       选取参数γ0 = 0.1，参数γ1=45,参数ρ取不同值，得到系统的开环频率特性以及闭环单位阶跃响应结果。

 

 

 ρ取不同值时云台系统的Bode图和闭环单位阶跃响应

      分析：固定权重系数γ0 ， γ1 不变时，增大权重系数ρ，系统的调节时间增大，截止频率也随之减小，说明系统的响应速度减慢了；而系统的超调量变化不大，幅值裕度随着权重系数的增大也相应的增大，即系统的稳定性增强。这些变化规律表明权重因子ρ牺牲系统的动态响应速度，获得一定的稳定裕度，因此在设计状态反馈时，权重系数ρ应该尽量取小值。

 分析参数γ0 的影响：

        选取参数ρ= 0.15，参数γ1=45,参数γ0取不同值，得到系统的开环频率特性以及闭环单位阶跃响应结果。 

 

γ0取不同值时云台系统的Bode图和闭环单位阶跃响应

        分析：增大权重系数γ0 ，系统的调节时间增大，截止频率也随之减小，说明系统的响应速度减慢了；而系统的超调量变化不大，幅值裕度随着权重系数的增大也相应的增大，即系统的稳定性增强。这表明权重因子γ0 牺牲系统的动态响应速度，获得一定的稳定裕度，因此在设计状态反馈时，权重系数γ0 应该尽量取小值。

分析参数γ1 的影响：

       选取参数ρ= 0.15，参数γ0=0.1,参数γ1 取不同值，得到系统的开环频率特性以及闭环单位阶跃响应结果。

  γ1 取不同值时云台系统的Bode图和闭环单位阶跃响应

        分析：增大权重系数γ1，系统的调节时间显著减小，截止频率也随之明显增大，说明系统的响应速度加快了；而系统的超调量变化不大，幅值裕度随着权重系数的增大而减小，即系统的稳定性降低。这表明权重因子γ1 牺牲系统的稳定裕度，以降低系统稳定性为代价来换取加快系统响应速度的目的。因此在设计状态反馈时，权重系数γ1 应该尽量取大点。

综上，可以拟定选择参数γ0 = 0.015，γ1  = 65，ρ = 0.01。

3. 状态观测器设计

        云台只有角度信息可以通过编码器进行测量，其他状态值都不可测，而设计状态反馈控制器需要知道每个状态的反馈值，因此需要设计状态观测器，用观测器估计出来的系统状态去替代实际系统的状态。

判断系统的能观性：

       构造系统的能观性矩阵：

 能观判别矩阵N的秩Rank(N) = 3，系统完全能观，可以构造全维状态观测器，则得到整个控制系统的Simulink结构图如图所示。

根据输出反馈控制结构框图可以容易写出观测器的状态方程如公式

 记观测误差 , 则有：

要使观测误差 渐进收敛为 0，则需要矩阵 ( A −LC) 的特征根均具由负实部。观测器的极点即为矩阵(A−LC)的全部特征根，当观测器的极点负实部离虚轴越远，则观测误差收敛速度越快，这样设计的观测器效果越好，当观测器的极点的负实部靠近虚轴或有正实部的极点时，误差收敛速度几乎没有变化或出现发散的情况，甚至于导致系统不稳定，因而必须选取合适的观测器极点。确定极点后便可以设计出状态观测矩阵 L。

根据前面的状态反馈设计和状态观测设计，选取了合适的权重系数γ0 = 0.015，γ1  = 65，ρ = 0.01，解对应的方程得到状态反馈矩阵：

K = [400810   4120   40   -640]

       因为观测器极点离虚轴越远，状态估计误差收敛的速度越快，故可以人为选取P1,2  = −59  ± 60 j, P3 = −60 作为观测器的极点，其对应的观测矩阵为

L = [1   0.017   -0.05]

 三、仿真结果

        通过改变 LQR 的控制权重系数γ0 ，γ1 ，ρ便可以改变系统的控制性能。由上述的控制变化规律，选取控制权重系数γ0 = 0.015，γ1  = 65，ρ = 0.01，此时系统的闭环阶跃响应和开环伯德图如图 ，其闭环阶跃响应的时域各项性能指标以及开环频域指标如表 。

引入状态观测器云台系统的闭环单位阶跃响应和Bode图

附录  求解反馈增益矩阵K的matlab程序

%权重因子
r0 = 0.1;r1 = 60;p = 0.15;
%权重因子变换对反馈矩阵的影响
%r0 = 0.1;r1 = 45;p = 0.01; K =  1.0e+05 *[2.2723    0.0211    0.0002   -0.0029]
%r0 = 0.1;r1 = 45;p = 0.15; K =  1.0e+05 *[1.2571    0.0161    0.0001   -0.0011]
%r0 = 0.1;r1 = 45;p = 0.50; K =  1.0e+04 *[8.9356    0.1249    0.0011   -0.0063]
%r0 = 0.1;r1 = 45;p = 1.00; K =  1.0e+04 *[7.3314    0.1065    0.0009   -0.0045]
%r0 = 0.1;r1 = 45;p = 5.00; K =  1.0e+04 *[4.6671    0.0722    0.0006   -0.0020]

%r0变化
%r0 = 0.01;r1 = 45;p = 0.15; K =  1.0e+05 *[1.2997    0.0175    0.0002   -0.0012] 
%r0 = 0.10;r1 = 45;p = 0.15; K =  1.0e+05 *[1.2571    0.0161    0.0001   -0.0011]
%r0 = 0.50;r1 = 45;p = 0.15; K =  1.0e+04 *[8.5072    0.0367    0.0007   -0.0063]
%r0 = 1.00;r1 = 45;p = 0.15; K =  1.0e+04 *[5.9610   -0.0259    0.0002   -0.0036]
%r0 = 5.00;r1 = 45;p = 0.15; K =  1.0e+04 *[2.4604   -0.0953   -0.0004   -0.0007]

%r1变化
%r0 = 0.10;r1 = 10;p = 0.15; K =  1.0e+04 *[5.4483    0.0740    0.0007   -0.0025]
%r0 = 0.10;r1 = 20;p = 0.15; K =  1.0e+04 *[7.8767    0.1057    0.0009   -0.0049]
%r0 = 0.10;r1 = 35;p = 0.15; K =  1.0e+05 *[1.0833    0.0141    0.0001   -0.0009]
%r0 = 0.10;r1 = 45;p = 0.15; K =  1.0e+05 *[1.2571    0.0161    0.0001   -0.0011]
%r0 = 0.10;r1 = 60;p = 0.15; K =  1.0e+05 *[1.4970    0.0186    0.0002   -0.0015]

%系统状态矩阵
A = [0, 1,0,0;
     0,0,1,0;
     0,-6756,-118.2,0;
     -6396,132,-1.2,0];
B = [0;0;1;0];
C = [6396,-132,1.2,0];
%计算目标函数J的相关系数
G = [C;r0*C*A;0,0,0,r1];
H = [0;r0*C*B;0];
I = 1;

Q = G'*G;
R = H'*H+p*I;
N = G'*H;
%求解Riccati方程，得到反馈增益矩阵
[K,S,E] = lqr(A,B,Q,R,N)

---

总结

提示：这里对文章进行总结：
例如：以上就是今天要讲的内容，本文仅仅简单介绍了LQR的使用。

参考文献：

[1]阳春分.二自由度云台视觉伺服系统研究与应用[D].华南理工大学,2017.

[2]王鹏飞. 二自由度云台视觉伺服控制系统的设计与实现[D].南京理工大学,2020.

作者：weibuweibu123