计算机控制系统信号恢复之零阶保持器

零阶保持器

在计算机控制系统中，由于CPU只能处理数字信号，而被控对象等过程往往是连续过程，因此计算机控制系统是一个混合系统，包含数字信号、模拟信号、离散模拟信号。而在数字信号通过DA转换为模拟信号的时候，样本点之间需要做连续处理，也就是保持器，保持器有很多种，根据其取Taylor展开的项数确定其为哪阶保持器。如果只取第一项就是零阶保持器。

零阶保持器传递函数推导

对零阶保持器的推导往往采用单位冲激响应，在0时刻给予输入 $\delta (t)$ ，则输出为：

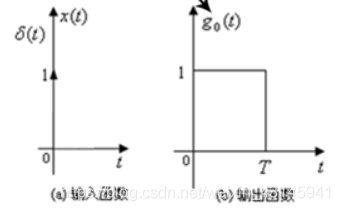
我们将这个输出分解为两个信号:

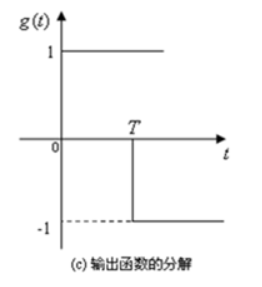
即 $g(t)=1(t)-1(t-T)$ 之后对其进行拉氏变换：$$L(g(t))=\frac{1}{s}-\frac{e^{-sT}}{s}=\frac{1-e^{-sT}}{s}$$
由于：$$L(\delta (t)=1$$
因此零阶保持器的传递函数就是 $L(g(t))$ 。

零阶保持器的频率响应

将 $L(g(t))$ 中的 $s$ 替换为 $jw$ 即可。于是得到：
$$W_{h0}(jw)=T\frac{sin(wT/2)}{wT/2}{e}^{-j\frac{wT}{2}}$$
观察这个式子我们发现当 $w$ 每到 $k{w}_S$ 的时候幅度就会发生正负跳变（$T=2\pi /w_S$），但与此同时后面的指数项角度也越过$-\pi$线，因此，我们将其表为如下式子：
$$W_{h0}(jw)=T|\frac{sin(wT/2)}{wT/2}|e^{j(-wT/2+k\pi )}$$
$$k=INT(w/w_S)$$
绘制图像如图：


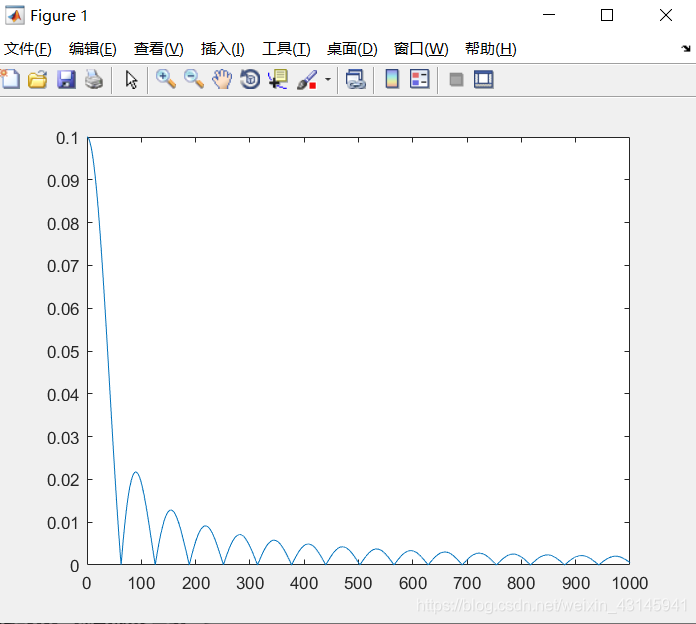
我们可以看到零阶保持器的相频特性呈锯齿状，我们也叫零阶保持器的开关特性，另外，零阶保持器有许多小旁瓣，但整体呈低通滤波特性。

零阶保持器的滞后特性

零阶保持器平均滞后 $T/2$ 。推导如下：
$$W_{h0}(s)=\frac{e^{Ts/2}-e^{-Ts/2}}{s{e}^{Ts/2}}=\frac{(1+Ts/2+...)-(1-Ts/2+...)}{s{e}^{Ts/2}}\approx T{e}^{-Ts/2}$$

总结

零阶保持器无论在计算机控制系统亦或是数字信号处理中都是一个至关重要的角色，深刻理解其物理背景和其对控制系统带来的影响是必须的。