Swin Transformer文章解读

小太阳啊！！

已于 2024-03-09 13:51:31 修改

阅读量915

点赞数 18

文章标签： transformer 深度学习人工智能计算机视觉

于 2024-03-09 13:50:38 首次发布

本文链接：https://blog.csdn.net/weixin_43238909/article/details/136581719

版权

摘要

将 Transformer 从语言转换为视觉的挑战源于两个领域之间的差异，例如视觉实体的规模变化很大，图像中的像素与文本中的单词相比分辨率很高。为了解决这些差异，提出了一种层次变换器，其表示使用移位窗口计算的。移位窗口方案通过将自注意力计算限制在不重叠的区域窗口上，同时还允许跨窗口连接，从而带来更高的效率。这种分层结构具有在各种尺度上建模的灵活性，并且具有相对于图像大小的线性计算复杂性。

1、介绍

在现有的基于 Transformer 的模型中， token 都是固定规模的，这一特性不适合这些视觉应用。另一个区别是，与文本段落中的单词相比，图像中的像素分辨率高得多。存在许多视觉任务，对于Transformer在高分辨率图像上来说是难以解决的，因为其自关注的计算复杂性与图像大小成二次方。为了克服这些问题，我们提出了一种通用的Transformer 主干，称为 Swin Transformer，它构造了层次特征图，并对图像大小具有线性计算复杂性。如图 1(a) 所示， Swin-Transformer 通过从小尺寸补丁（灰色轮廓）开 始，逐渐合并更深的 Transformer 层中的相邻补丁 ，构建一个层次表示。

有了这些分层特征图

总结

Swin Transformer 通过从较小尺寸的 patch （灰色轮廓）开始，逐渐在更深的 transformer 层中合并 相邻 patch ，从而构造出一个层次化表示。有了这些层次化特征就可以继续使用 FPN 或 U-net 等操作了。 线性复杂度是通过在非重叠窗口内，局部地计算自注意力来实现的（红色轮廓 ) ，而非整张图片的所有 patch 上进行的 。

Swin-Transformer 模型可以方便的利用高级技术进行密集预测，如特征融合网络（ FPN ）或 U-Net 。

线性计算复杂度是通过在划分图像（红色轮廓）的非重叠窗口内局部计算自注意来实现的 。每个窗口的patch是固定的，因此复杂性和图像大小成线性关系。这些优点使 swin Transformer 适合作为各种视觉任务的通用主干，与之前基于Transformer 的架构形成对比，后者产生单一分辨率的特征图，并具有二次复杂性。

Swin-Transformer 的一个关键设计元素是 它在连续的自注意层之间移动窗口分区 ，如图 2 所示。偏移的窗口桥接了前一层的窗口，提供了它们之间的连接，显著增强了建模能力。这种策略在实际延迟方面也很有效：一个窗口内的所有查询补丁共享相同的密集集，这有助于硬件中的内存访问。相反，早期的基于滑动窗口的自注意方法由于不同查询像素的不同密钥。

所提出的 Swin Transformer 在图像分类、目标检测和语义分割等识别任务上取得了很强的性能。它在三项任务上的延迟相似，显著优于ViT/DeiT 和 ResNe(X)t 模型。

总结

另一个关键设计元素是：它在连续自注意层之间窗口分区的移位，如图 2 所示，移位窗口桥接了前一层的窗口，提供二者之间的连接，显著增强建模能力。这种策略对现实世界的延迟也是有效的：一个局部窗口内的query patch 共享相同的 key 集合。

2、方法

3.1整体架构

Swin Transformer 体系结构的概述如图 3 所示，其中说明了微小版本（ Swin-T) 。

它首先通过像 ViT 这样的 patch 拆分模块 将输入 RGB 图像分割成不重叠的补丁 。将输入的 HXWx3 的 RGB图像拆分成非重叠尺寸的 $N\times (P^2 \times 3)$ patch。每个 $P^3 \times 3$ Patch 都被视为一个 patch token 。共拆分出 N个。更具体的，用 $P^2 = 4 \times 4$ 且通道数 C=3 的 patch ，故各 patch 展平后的特征维度为 PXPXC=4x4x3=48，共有 $N = \frac{H}{4} \times \frac{W}{4} = \frac{HW}{16}$ 个 patch token 。换言之，每张

HXWx3的图片被处理为了 $\frac{H}{4} \times \frac{W}{4}$ 个图片的 patches ，每个 patch 被展平为 48 维的 token 向量，整

体上是一个展平的 $N\times (P^2 \times 3) = (\frac{H}{4}\times \frac{W}{4}) \times 48$ 维 2Dpatch序列。线性嵌入层（Linear Embedding）（即全连接层）则将此时维度为 $(\frac{H}{4}\times \frac{W}{4}) \times 48$ 张量投影到任意维度C，得到维度为 $(\frac{H}{4}\times \frac{W}{4}) \times C$ 的 Linear Embedding。

随后这些 patch token （此时已为 Linear Embedding ）被馈入若干具有改进自注意力的 Swin

Transformer blocks 。首个 Swin Transformer block 保持输入输出 tokens数恒为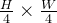 $\frac{H}{4}\times \frac{W}{4}$ 不变。

与线性嵌入一起被称为 “stage 1" （图 3 的第一个虚线框所示）。

为了产生层次化表示 ，随着网络的深入， tokens 数通过 patch 合并层来减少数量。第一个补丁合并层将每组2x2 个相邻补丁的特征连接起来，则 patch token 数变为原来的1/4，即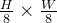 $\frac{H}{8}\times \frac{W}{8}$ ，而

patch token 的维度则扩大四倍，即 4C 。然后对 4 维的 patch 拼接特征使用了一个线性层，将输出维度降为 2C 。然后使用 Swin Transformer blocks作为特征转换，其分辨率保持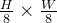 $\frac{H}{8}\times \frac{W}{8}$ 不变。

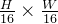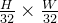首个 patch 合并层和该特征转换 Swin Transformer blocks 的第一块被表示为 ”stage 2"( 图 3 中的第二个 虚线框 ) 。该程序重复两次，分别为 “stage 3"和”stage 4"，输出分辨率分别为 $\frac{H}{16}\times \frac{W}{16}$ 和 $\frac{H}{32}\times \frac{W}{32}$ 每个 stage 都会改变张量的维度 ，从而形成一种层次化的表征。

Swin Transformer 块： Swin Transformer 是通过 Transformer 中的标准多头自注意（ MSA ）模块替换 为基于移动窗口的模块所构建的， 其他层保持不变。如图 3(b) 所示， Swin Transformer 由一个基于移动窗口的MSA 模块组成，然后是一个中间具有 GELU 非线性的 2 层 MLP 。在每个 MSA 模块和每个 MLP 之前应用LayerNorm ，在每个模块之后应用剩余连接。 Swin Transformer block : 与 Transformer 相比，将标准多头自注意模块（ MSA ）替换为基于移动窗口的多头自注意模块（W-MSA/SW-MSA ）且保持其他部分不变。

3.2 基于移动窗口的self-attention

标准 Transformer 架构及其对图像分类的自适应都进行全局自注意，其中计算 1token 和所有其他 token 之间的关系。全局计算导致了token 数量的二次复杂度，使其不适合于许多需要大量 token 进行密集预测或表示高分辨率图像的视觉问题。

非重叠窗口中的 self-attention 为了有效建模，我们建议在局部窗口内计算 self-attention 。窗口被布置为非重叠的方式均匀地划分图像。假设每个窗口包含MXM 个补丁，则全局 MSA 模块和基于窗口的 MSA模块的计算复杂度关于hxw补丁的图像：

其中前者是补丁数 hw 的二次方，而后者在 M 固定（默认为 7 ）时是线性的，全局自注意计算对于大型硬件来说通常还是负担不起的，而基于窗口的自注意是可扩展的。

连续块中的移位窗口分区 基于窗口的自我关注模块缺乏跨窗口的连接，这限制了其建模能力。为了引入跨窗口连接，同时保持非重叠窗口的有效计算，我们提出了一种移位窗口分区方法 ，该方法在连续 Swin Transformer块中的两种分区配置之间交替。

如图 2 所示， 第一个模块 使用从左上角像素开始的规则窗口划分策略，将 8x8 的特征图均匀地划分为大小 为 4x4(M=4) 的 2x2 个窗口（此时局部窗口尺寸为 M=4 ））。然后， 下一个 模块通过 将窗口从规则划分的窗口移位 $(\left \lfloor \frac{M}{2},\frac{M}{2} \right \rfloor)$ 个像素。采用与前一层的窗口配置不同的窗口配置。

使用移位窗口划分方法，两个连续的 Swin-Transformer 块计算如下：

其中 $\hat{Z}^l$ 和 $Z^l$ 分别表示块 l 的 (S)W-MSA 和 MLP 模块的输出特征； W-MSA 和 SW-MSA 分别表示

使用规则和移位窗口划分配置的基于窗口的多头自注意。

移位窗口划分方法引入了前一层中相邻非重叠窗口之间的连接，并被发现在图像分类、对象检测和语义分割方面是有效的。

针对移位配置的高效批量计算

移位窗口划分的一个问题是，它将导致更多的窗口，从移位配置中的

$\left \lceil \frac{h}{M} \right \rceil \times \left \lceil \frac{w}{M} \right \rceil$ 到 $(\left \lceil \frac{h}{M} \right \rceil +1) \times (\left \lceil \frac{w}{M} \right \rceil +1)$ , 并且一些窗口将小于 MXM 。一个简单的解决方案是将较小的窗口填充到 MXM 的大小，并在计算注意力时屏蔽填充的值。当常规分区中的窗口数量较少时，例如 2x2 ，这种朴素解增加的计算量是相当大的 $(2 \times 2 \rightarrow 3 \times 3)$ 。在这里，我们提出了一种更有效的批量计算方法，通过向左上角方向循环移位，如图 4 所示。在该偏移之后，分批窗口可以由在特征图中不相邻的几个子窗口组成，因此采用掩蔽机制来将自注意力计算限制在每个子窗口内。通过循环移位，批处理窗口的数量与常规窗口分区的数量保持相同，因此也是有效的，这种方法的低延迟如表 5 所示。

此外，我们提出了一种更有效的批计算方法，其循环向左上方移位，如图 4 所示。在这种移位后，批窗口可由特征图中不相邻的子窗口组成，因此，使用屏蔽机制将自注意计算限制在每个子窗口内。通过循环移位，批处理窗口的数仍与规则分区的窗口数相同（如规则划分时是4 个窗口，向左上角循环移位后仍是4个窗口，如上图的 A,B,C,D 所示）。因此，该方法是有效的。

经过循环移位的方法，一个窗口可包含来自不同窗口的内容。因此，要采用 masked MSA 机制将自注意力计算限制在各子窗口内，最后通过逆循环移位方法将每个窗口的自注意力结果返回。例如，一个9 窗口的图解如下所hi ：

按子窗口划分即可得到 5 号子窗口的自注意结果，但直接计算会使得 5 号 /6 号 /4 号子窗口的自注意力计算混在一起，类似的混算还包括5 号 /8 号 /2 号子窗口和 9 号 /7 号 /3 号 /1 号子窗口的纵向或横向等。所以需采用masked MSA 机制：先正常计算自注意力，再进行 mask 操作将不需要的注意力图置 0 ，从而将自注意力计算限制在各子窗口内。

例如， 6 号 /4 号子窗口共由 4 个 patch 构成一个正方形区域，如下所示，故应计算出 4x4 注意力图。

为避免各不同的子窗口注意力计算发生混叠，合适的注意力图应如下所示

从而，合适的 mask 应如下所示：

官网的掩码图

第一轮 i_s=0 ir =0 s1_1 : 融合 i_r=1: s1_2: 融合

小太阳啊！！

关注

18
点赞
踩
22

收藏

觉得还不错? 一键收藏
0
评论
Swin Transformer文章解读

从语言转换为视觉的挑战源于两个领域之间的差异，例如视觉实体的规模变化很大，图像中的像素与文本中的单词相比分辨率很高。偏移的窗口桥接了前一层的窗口，提供了它们之间的连接，显著增强了建模能力。在这种移位后，批窗口可由特征图中不相邻的子窗口组成，因此，使用屏蔽机制将自注意计算限制在每个子窗口内。所示，移位窗口桥接了前一层的窗口，提供二者之间的连接，显著增强建模能力。）时是线性的，全局自注意计算对于大型硬件来说通常还是负担不起的，而基于窗口的自注意是可扩展的。经过循环移位的方法，一个窗口可包含来自不同窗口的内容。
复制链接

扫一扫