《视觉SLAM十四讲 第二版》课后习题

本文为《视觉SLAM十四讲》(第二版)的课后习题解答，为本人学习时参考着网上的资源所写的答案，可能有所纰漏，希望大家指出。

第1讲 预备知识

1. 有线性方程 Ax = b,当我们知道 A, b,想要求解 x 时,如何求解?这对 A 和 b 需 要哪些条件?提示:从 A 的维度和秩角度来分析。
   1.若b≠0，则
   当r=m=n时，整个方程存在唯一解；
   当r=n<m，即A列满秩，整个方程要么无解要么存在唯一解；
   当r=m<n，即A行满秩，整个方程有无穷解；
   当r<m,r<n，整个方程要么无解要么存在唯一解。
   2.若b=0，则
   当r=n时，整个方程只有解x=0；
   当r<n，整个方程有无穷解；
2. 高斯分布是什么?它的一维形式是什么样子?它的高维形式是什么样子?
   答：高斯分布又称正态分布，一维形式为概率密度函数…

第2讲 初始SLAM

第3讲 三维空间刚体运动

1. 验证旋转矩阵是正交矩阵。
   
2. 验证四元数旋转某个点后,结果是一个虚四元数(实部为零),所以仍然对应到一个三维空间点(式 3.34)
   
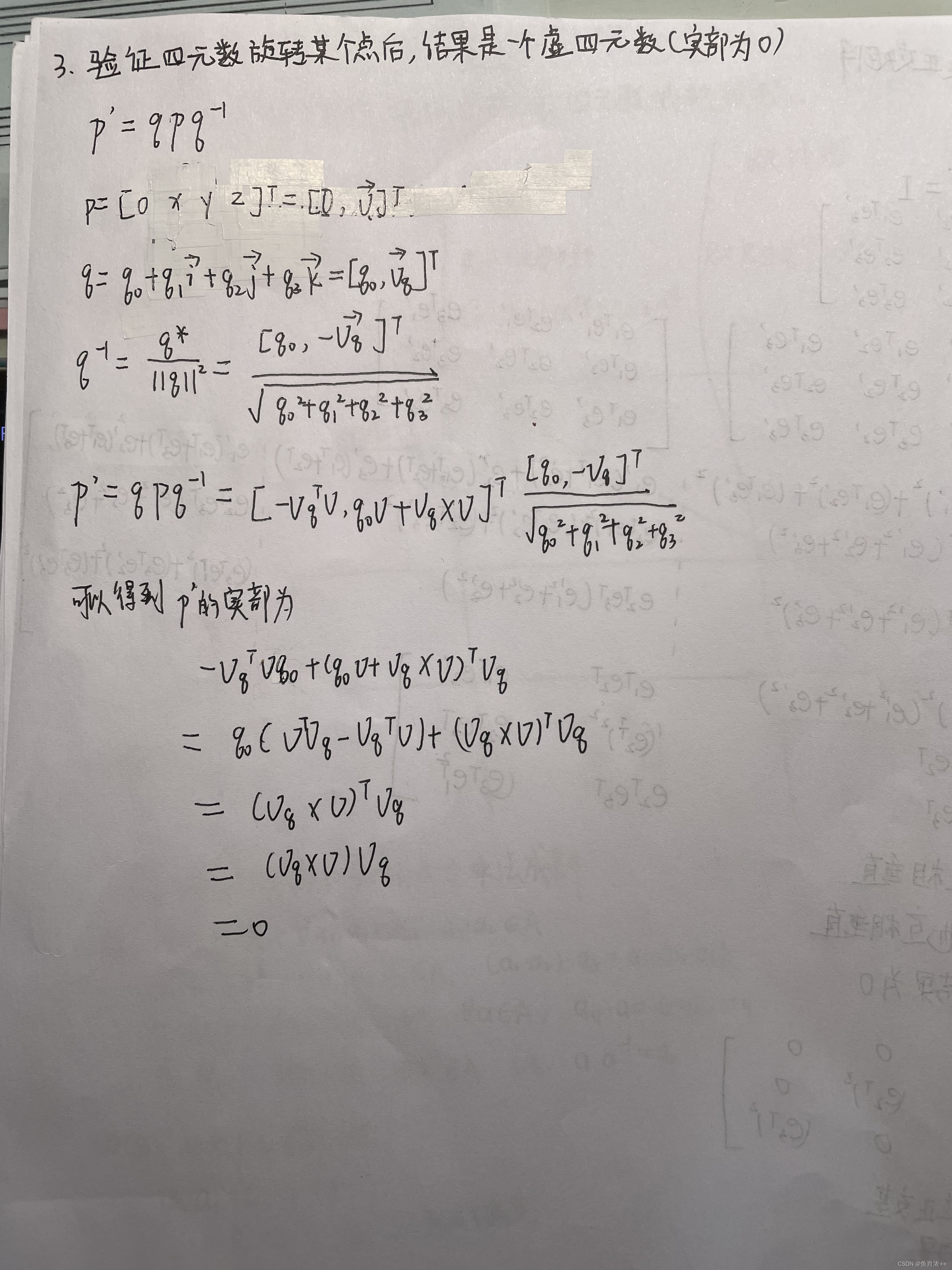
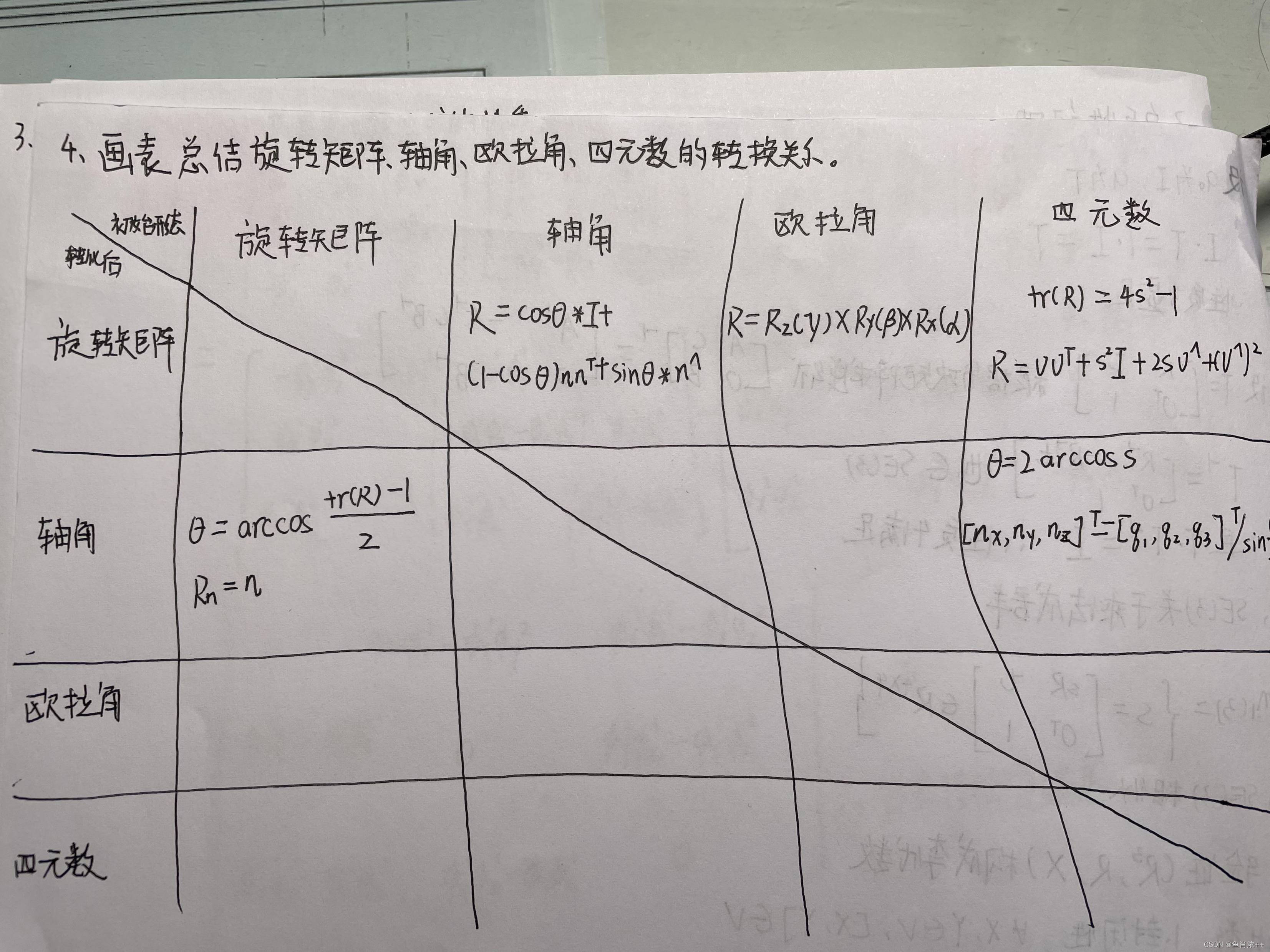
3. 画表总结旋转矩阵、轴角、欧拉角、四元数的转换关系。
   

第4讲 李群与李代数

1.验证SO(3),SE(3)和Sim(3)关于乘法成群


2.验证（R^3,R,X)构成李代数

3.验证so(3)和se(3)(李代数）满足李代数要求的性质




4.验证性质(4.20)和(4.21)

5.证明

6.证明

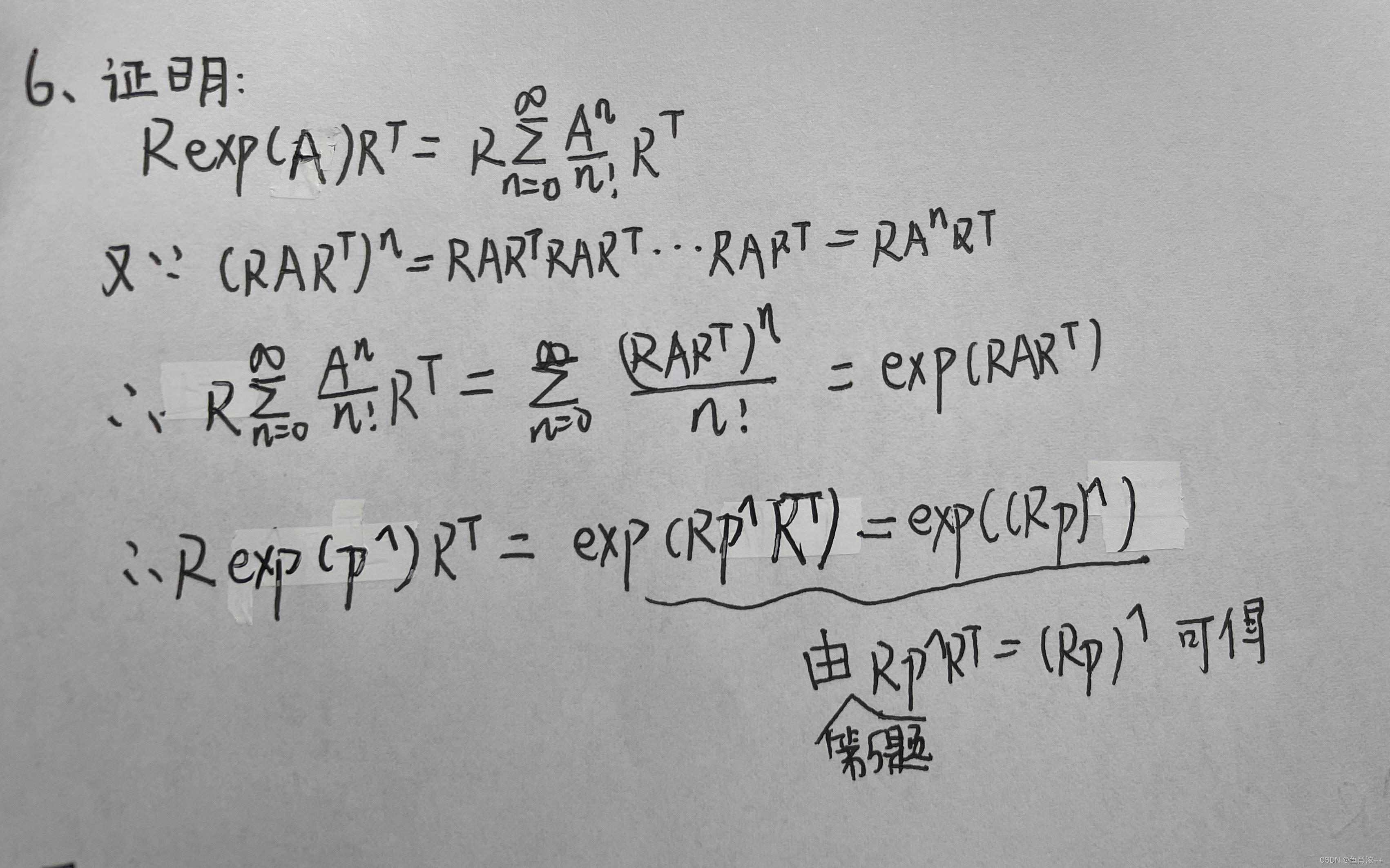
7 仿照左扰动的推导，推导SO(3)和SE(3)在右扰动下的导数。

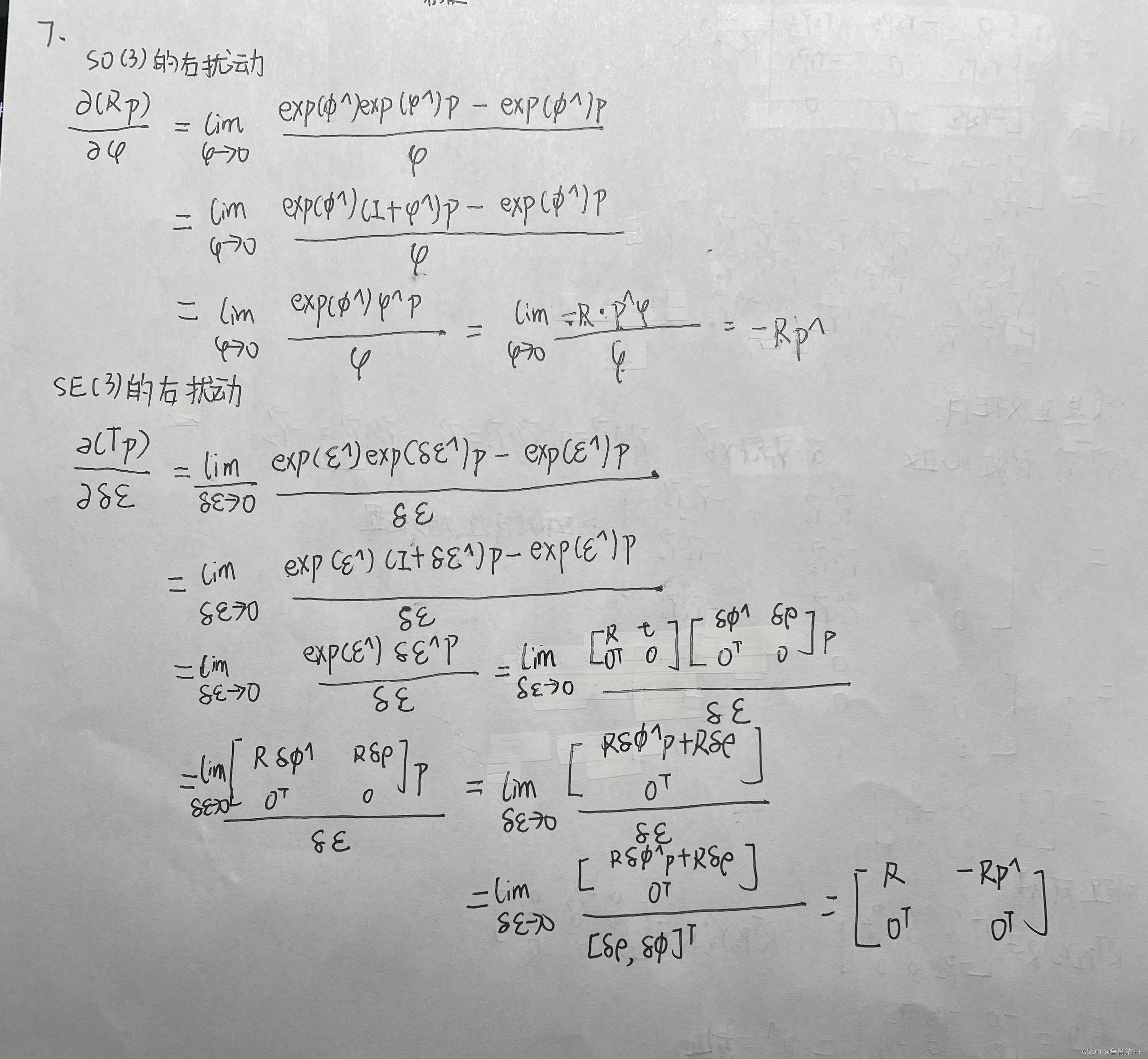
第5讲 相机与图像

第6讲 非线性优化

1. 证明线性方程Ax = b 当系数矩阵A 超定时，最小二乘解为
   
2. 调研最速下降法、牛顿法、高斯牛顿法和列文伯格-马夸尔特方法各有什么优缺点？除了我们举例的Ceres库和g2o库，还有哪些常用的优化库？
   
3. 为什么高斯牛顿法的增量方程系数矩阵可能不正定？不正定有什么几何含义？为什么在这种情况下解就不稳定了？

5. DogLeg是什么？它与高斯牛顿法和列文伯格-马夸尔特方法有什么异同？

第7 讲 非线性优化

1. 除了本书介绍的ORB特征点，你还能找到哪些特征点？请说说SIFT或SURF的原理，并对比它们与ORB之间的优劣。

2. 设计程序调用OpenCV中的其他种类特征点，统计在提取1000个特征点时在你的机器上所用的时间。

3. 我们发现，OpenCV提供的ORB特征点在图像中分布不够均匀。你是否能够找到或提出让特征点分布更均匀的方法？

4. 研究FLANN为何能够快速处理匹配问题，除了FLANN，还有哪些可以加速匹配的手段？

5. 把演示程序使用的EPnP改成其他PnP方法，并研究它们的工作原理。

6. 在PnP优化中，将第一个相机的观测也考虑进来，程序应如何书写？最后结果会有何变化？

7. 在ICP程序中，将空间点也作为优化变量考虑进来，程序应如何书写？最后结果会有何变化？

8. 在特征点匹配过程中，不可避免地会遇到误匹配的情况。如果我们把错误匹配输入到PnP或ICP中，会发生怎样的情况？你能想到哪些避免误匹配的方法？

9. 使用Sophus的SE3类，自己设计g2o的节点和边，实现PnP和ICP的优化。

10. 在Ceres中实现PnP和ICP的优化。