Robot dynamics lecture 3

3.1 Introduction

对于fixed-based 动力学系统，可以用下面这个表达式。
$$M(q)\ddot{q}+b(q,\dot{q})+g(q)=\tau +J_c(q{)}^T{F}_c$$

有三种方法：1.newton-euler 法, 使用笛卡尔坐标系；2.Lagrange Methods， 使用广义坐标系; 3. Projected Newton-Euler methods。

3.2 Foundation from Classical Mechanics

3.2.1 粒子的力学

对于单个质点，在运动过程中没有任何几何学上的限制，通过牛顿第二定律既可以刻画。
$$\ddot{r}m=F$$

对于一个有几何形状的物体，将其看成一个个质点组合而成
$$\ddot{r}dm=dF$$

对于线性运动，可以看成一个质量放在质心处的单个物体，满足$\ddot{r}m=F$。

3.2.2 virtual Displacements

质点之间内部作用力对系统运动的影响，可以用虚位移方法进行分析。
定义轨迹方程,和joint角度q和时间t有关
$$r=r(q,t)$$

通过微分形式得到结果：
$$\delta r(q,t)=\sum _{k=1}^{n_q}\frac{\delta r}{\delta q_k}\delta q_k$$

3.2.3 virtual displacement of single rigid bodies

下图是一个简单的系统，画出两个系统中的两个质点，dm和S的质点。

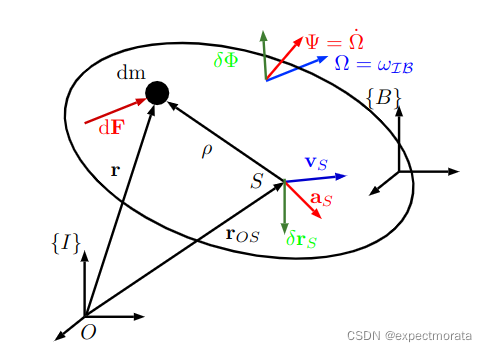
从运动基础上进行分析,相对距离始终恒定，这里的$\rho$是惯性坐标系的向量。
$$\begin{array}{rl}\vec{r}& ={\vec{r}}_{os}+\vec{\rho }\\ \dot{\vec{r}}& ={\vec{v}}_{os}+\vec{\Omega }\times \vec{\rho }=\left[\begin{array}{cc}{I}_{3\times 3}& -[\rho {]}_{\times }\end{array}\right]\left[\begin{array}{c}{v}_{os}\\ \Omega \end{array}\right]\\ \ddot{r}& ={\vec{a}}_{os}+\vec{\Psi }\times \vec{\rho }+\vec{\Omega }\times \vec{\Omega }\times \vec{\rho }\\ & =\left[\begin{array}{cc}{I}_{3\times 3}& -[\rho {]}_{\times }\end{array}\right]\left[\begin{array}{c}{a}_s\\ \Psi \end{array}\right]+\vec{\Omega }\times \vec{\Omega }\times \vec{\rho }\end{array}$$
得到差分形式：
$$\delta \vec{r}=\delta {\vec{r}}_s+\vec{\delta }\varphi \times \vec{\rho }=\left[\begin{array}{cc}{I}_{3\times 3}& -[\rho {]}_{\times }\end{array}\right]\left[\begin{array}{c}\delta r_s\\ \delta \varphi \end{array}\right]$$

3.2.4 virtual displacement of multi body system

对于一个多刚体系统，关节运动的限制，使得关节的速度末端的速度的映射关系如下：
$$\left[\begin{array}{c}{v}_s\\ \Omega \end{array}\right]=\left[\begin{array}{c}{J}_P\\ J_R\end{array}\right]\dot{q}$$
进行差分，得到结果
$$\left[\begin{array}{c}{a}_s\\ \Psi \end{array}\right]=\left[\begin{array}{c}{J}_P\\ J_R\end{array}\right]\ddot{q}+\left[\begin{array}{c}{\dot{J}}_P\\ {\dot{J}}_R\end{array}\right]\dot{q}$$

用虚位移角度来看，
$$\left[\begin{array}{c}\delta r_s\\ \delta \Theta \end{array}\right]=\left[\begin{array}{c}{J}_P\\ J_R\end{array}\right]\delta q$$

3.2.5 虚功原理

限制力在限制点所做的功为0之和为0
$$\delta w=\delta {\vec{r}}_c^T\cdot {\vec{F}}_c=0$$
使用达朗贝尔原理，对于一个刚体，功的微分满足：
$$\delta W={\int }_B\delta r^T\cdot (\ddot{\vec{r}}dm-d{F}_{ext})=0$$

对于任意的$\delta r$，虚功原理均成立。

3.3 牛顿欧拉法

3.3.1 单个刚体

使用虚功原理
$$\begin{array}{rl}0& =\delta W={\int }_B{\left[\begin{array}{c}\delta r_s\\ \delta \Theta \end{array}\right]}^T\left[\begin{array}{c}{I}_{3\times 3}\\ [\rho {]}_{\times }\end{array}\right](\left[\begin{array}{cc}{I}_{3\times 3}& -[\rho {]}_{\times }\end{array}\right]\left[\begin{array}{c}{a}_s\\ \Psi \end{array}\right]dm+[\vec{\Omega }{]}^2\times \vec{\rho }dm-d{F}_{ext})\\ & ={\left[\begin{array}{c}{r}_{os}\\ \Theta \end{array}\right]}^T{\int }_B(\left[\begin{array}{cc}{I}_{3\times 3}dm& [\rho {]}_{\times }^{T}dm\\ [\rho {]}_{\times }dm& -[\rho {]}_{\times }^{2}dm\end{array}\right]\left[\begin{array}{c}{a}_s\\ \Psi \end{array}\right]+(\left[\begin{array}{c}[\vec{\Omega }{]}_{\times }^2\vec{\rho }dm\\ [\rho {]}_{\times }[\vec{\Omega }{]}_{\times }^2\vec{\rho }dm\end{array}\right])-(\left[\begin{array}{c}d{F}_{ext}\\ [\rho {]}_{\times }d{F}_{ext}\end{array}\right])\end{array}$$

叉乘满足下列的关系$a\times (b\times (b\times a))=-b\times (a\times (a\times b))$,积分公式满足
$$\begin{array}{rl}{\int }_{B}dm& =:mbodymass\\ {\int }_B\vec{\rho }dm& =0S=COG,S是中心点\\ {\int }_B-[\rho {]}_{\times }^{2}dm& ={\int }_B[\rho {]}_{\times }[\rho {]}_{\times }^{T}dm=:{\Theta }_s转动惯量COG\end{array}$$

上面的公式，简化的结果是：
$$0=\delta W={\left[\begin{array}{c}\delta r_s\\ \delta \Phi \end{array}\right]}^T((\left[\begin{array}{cc}{I}_{3\times 3}m& 0\\ 0& {\Theta }_s\end{array}\right]\left[\begin{array}{c}{a}_s\\ \Psi \end{array}\right]+(\left[\begin{array}{c}0\\ [\Omega {]}_{\times }{\Theta }_s\Omega \end{array}\right])-(\left[\begin{array}{c}{F}_{ext}\\ {\mathrm{T}}_{ext}\end{array}\right]))$$

为了往多刚体进行扩张，引入变量
$$\begin{array}{rl}{P}_S& =m{\vec{v}}_{s}linearmomentum\\ N_S& ={\Theta }_S\cdot \Omega angularmomentumaroundCOG\\ {\dot{P}}_S& =m{\vec{a}}_{s}changeinlinearmomentum\\ {\dot{N}}_S& ={\Theta }_S\cdot \Psi +\Omega \times {\Theta }_S\cdot \Omega changeinangularmomentum\end{array}$$
对上面的公式再进行简化：
$$0=\delta W={\left[\begin{array}{c}\delta r_s\\ \delta \Phi \end{array}\right]}^T((\left[\begin{array}{c}{\dot{P}}_s\\ {\dot{N}}_S\end{array}\right])-(\left[\begin{array}{c}{F}_{ext}\\ {\mathrm{T}}_{ext}\end{array}\right]))\forall (\left[\begin{array}{c}\delta r_s\\ \delta \Phi \end{array}\right])$$
根据上面这个公式，得到了牛顿欧拉公式
$$\begin{array}{rl}{\dot{P}}_S& =F_{ext,S}\\ {\dot{N}}_S& =T_{ext}\end{array}$$

$F_{ext}$是外力作用在COG上结果，$T_{ext}$是转矩合力，如果$F_{ext}$不是直接作用在COG上，就将其看成是作用在质心的力和转矩。如果constraint作用没有作用在COG上，分析在constraints点的转动惯量满足。
$${}_B\Theta =C_{BA}{\cdot }_A\Theta \cdot C_{BA}^T$$

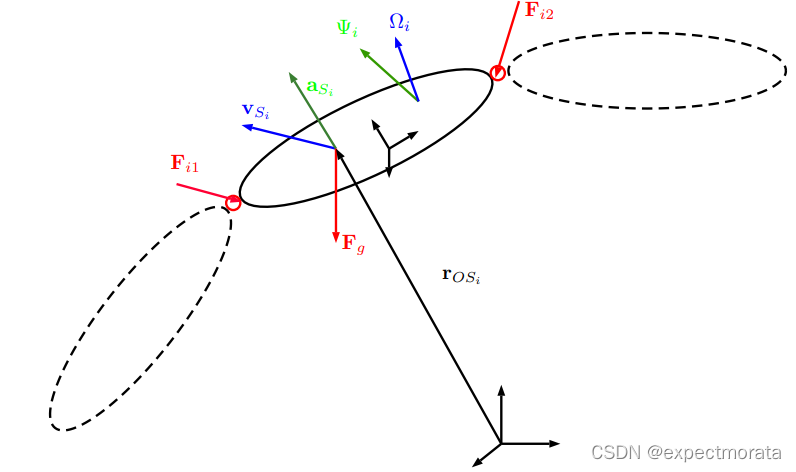
3.3.2 多刚体

对于多刚体，在joint处，进行切割，将其看成n个刚体。
对于$n_j$个广义坐标系，有$6n_j$个方程，再有$5n_j$个限制力。手算起来还是很复杂。

3.4 Lagrange Methods

3.4.1 基础概念

几个基础概念：

• 广义坐标系和广义速度
• 拉格朗日方程：
  $$\begin{array}{rl}L& =\mathrm{T}-U\\ \frac{d}{dt}(\frac{\partial L}{\partial \dot{q}})-(\frac{\partial L}{\partial q})& =\tau \end{array}$$

3.4.2 动能

系统的动能是各个关节

只要找到其中线速度和角速度是惯性系统的绝对速度，对于多刚体系统，joint的线速度和角速度是一个间接的结果，需要转换得到$\dot{q}$。
$$\begin{array}{rl}{\dot{r}}_{si}& =J_{Si}\dot{q}\\ {\Omega }_{si}& =J_{Ri}\dot{q}\end{array}$$
广义系统的动能：
$$T(q,\dot{q})=0.5{\dot{q}}^T(\sum _{i=1}^{n_b}(J_{Si}^T{m}_i{J}_{Si}+J_{Ri}^T{\Theta }_{Si}{J}_{Ri}))\dot{q}=0.5\ast {\dot{q}}^{T}M(q)\dot{q}$$

非线性离心力和科里奥利力由该公式差分得到的。

3.4.3 Potential Energy

势能由重力势能和弹性势能组成，考虑到势能场的不均匀性，重力可以表示为：
$$\begin{array}{rl}{F}_{gi}& =m_i{g}_I{e}_g\\ u_g& =-\sum _{i=1}^{n_b}{r}_{Si}^T{F}_{gi}\\ u_{Ej}& =0.5k_j(d(q)-d_0{)}^2\end{array}$$

3.4.4 External forces

所有外力做功，均可看成是广义力做功的效果。

3.4.5 额外的限制

对于fixed-based system, 只要通过广义坐标系，就可以避开限制力。对于float-based system, 例如足式机器人，只有接触到地面才会有限制力作用，采用拉格朗日乘子解决该问题,用线性表达运动限制。
$$\begin{array}{rl}& \sum _{k=1}^{n_q}{a}_{k,j}(q){\dot{q}}_k+a_{0,j}(t),j=1,2,...,n_{c,m}\\ & J_m=\left[\begin{array}{ccc}{a}_{1,1}& ...& a_{1,n_{c,m}}\\ ...& ...& ...\\ a_{n_q,1}& ...& a_{n_q,n_{c,m}}\end{array}\right]\end{array}$$

改良后的constrained culer-lagrange (CEL),公式如下：
$$\frac{d}{dt}(\frac{\partial L}{\partial \dot{q}})-(\frac{\partial L}{\partial q})+J_m^T{\lambda }_m+(\frac{\partial f_c}{\partial q}{)}^T{\lambda }_c=\tau$$

3.5 Projected Newton-Euler method

结合牛顿欧拉法分析在笛卡尔坐标系和广义坐标系。
$$M(q)\ddot{q}+b(q,\dot{q})+g(q)=\tau +J_c^{T}Fc$$

3.5.2 获取运动的广义方程

从牛顿欧拉法开始，获取基础公式，根据3.2.4 部分得到的结果。
$$\begin{array}{rl}\left[\begin{array}{c}{\dot{P}}_{Si}\\ {\dot{N}}_{Si}\end{array}\right]& =\left[\begin{array}{c}m{a}_{Si}\\ {\Theta }_{Si}{\Psi }_{Si}+{\Omega }_{Si}\times {\Theta }_{Si}{\Omega }_{Si}\end{array}\right]\\ & =\left[\begin{array}{c}m{J}_{Si}\\ {\Theta }_{Si}{J}_{Ri}\end{array}\right]\ddot{q}+\left[\begin{array}{c}m{\dot{J}}_{Si}\dot{q}\\ {\Theta }_{Si}{\dot{J}}_{Ri}\dot{q}+J_{Ri}\dot{q}\times {\Theta }_{Si}{J}_{Ri}\dot{q}\end{array}\right]\end{array}$$
虚功原理如下：
$$\begin{array}{rl}0=\delta W& =\sum _{i=1}^{n_b}{\left[\begin{array}{c}\delta r_{si}\\ \delta \Phi i\end{array}\right]}^T((\left[\begin{array}{c}{\dot{P}}_{Si}\\ {\dot{N}}_{Si}\end{array}\right])-(\left[\begin{array}{c}{F}_{ext,i}\\ {\mathrm{T}}_{ext,i}\end{array}\right]))\forall (\left[\begin{array}{c}\delta r_s\\ \delta \Phi \end{array}\right])\\ & =\delta q^T\sum _{i=1}^{n_b}((\left[\begin{array}{c}{\dot{P}}_{Si}\\ {\dot{N}}_{Si}\end{array}\right])-(\left[\begin{array}{c}{F}_{ext,i}\\ {\mathrm{T}}_{ext,i}\end{array}\right]))\forall \delta q\end{array}$$
得到最终的结果：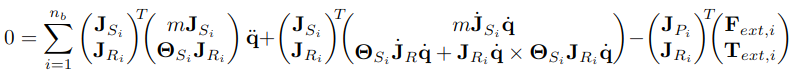
再对比原始公式：
$$\begin{array}{rl}M& =\sum _{i=1}^{n_b}(J_{Si}^{T}m{J}_{Si}+J_{Ri}^T{\Theta }_{Si}{J}_{Ri})\\ b& =\sum _{i=1}^{n_b}(J_{Si}^{T}m{\dot{J}}_{Si}\dot{q}+J_{Ri}^T({\Theta }_{Si}))\\ g& =\sum _{i=1}^{n_b}-J_{Si}^T{F}_{g,i}\end{array}$$

上面公式通过joint将每个link当成单独的个体来分析，所以使用的角速度和线速度都是绝对值。

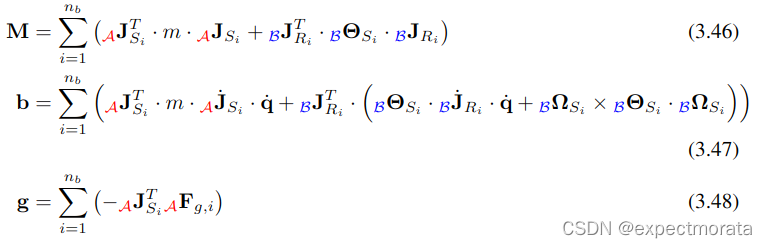
公式中的$Jsi$和$Jri$是对应关节的质心相对于机器人base_link的jacobian矩阵，这个是狠明确的。
公式中的$\Theta s_i$的坐标系要如何确定？
从转动惯量的定义出发，使用角动量$H=\Theta \vec{w}$描述刚体的旋转运动。
projected newton euler法来说，坐转动惯量标系选取：
1）和joint对应的坐标系方向一致；
2）坐标系原点在刚体的质心上；

3.5.3 External Force

通过jacobian 矩阵，将笛卡尔坐标系上的受力和转矩转换到广义坐标系上。
$$\begin{array}{rl}{\tau }_{F,ext}& =\sum _{j=1}^{n_{f,ext}}{J}_{P,j}^T{F}_j\\ {\tau }_{T,ext}& =\sum _{k=1}^{n_{f,ext}}{J}_{R,k}^T{F}_k\\ {\tau }_{ext}& ={\tau }_{F,ext}+{\tau }_{T,ext}\end{array}$$

安装在joint上的驱动关节，同时对两个link进行做功，做功的方向相反，驱动力对广义的效果。
$$\begin{array}{rl}{\tau }_{a,k}& =(J_{s_k}-J_{s_{k-1}}{)}^T{F}_{a,k}+(J_{R_k}-J_{R_{k-1}}{)}^T{T}_{a,k}\\ \tau & =\sum _{k=1}^{n_A}{\tau }_{a,k}+{\tau }_{ext}\end{array}$$

• 注意事项
  计算广义外力的作用效果${\tau }_{ext}$时，有两种方法：
  1）直接用$J_{P,i}^{\prime }\ast F_{ext}$
  2）随便选择一个link, 将$F_{ext}$转换到link质心的受力和作用力偶$T_{ext}$，再使用$js{i}^{\prime }\ast F_{ext}+jr{i}^{\prime }\ast T_{ext}$
• 计算内力的作用效果${\tau }_{a,k}$,
  step1: 拆解成分别作用于两个link的一对反作用力，分别将作用力，转换到对应link质心的作用力和作用力偶
  step2: 使用$js{i}^{\prime }\ast F_{ext}+jr{i}^{\prime }\ast T_{ext}$进行求解