三维射影变换
三维射影变换是射影空间上的可逆齐次线性变换,这个变换可由
4
×
4
的矩阵
H 来描述:X
′ =
H
X
矩阵
H 称为射影变换矩阵或称为单应矩阵。三维射影变换有
15
个自由度
5 点确定三维射影变换:如果
5
个点对应中任意
4
点不共面,则它们唯一确定一个三维射影变换
平面与直线的变换规则
射影变换 H 对平面的变换规则是
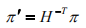
射影变换
H
对直线 L 的变换规则是
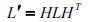
其对偶形式是:

二次曲面与变换规则
二次曲面方程所定义:
 ,其
中
Q
是
4
×
4 的对称矩阵
,其
中
Q
是
4
×
4 的对称矩阵
如果
Q
是降秩的,则称它为退化二次曲面,否则称为非退化二次曲面
二次曲面的一些常用性质:
1. 二次曲面有
9
个自由度,即由它的
10
个不同元素的比值所确定,因此空间中
9 个点可确 定一个二次曲面;如果二次曲面是退化的,则可用较少的点来确定;
2. 直线与二次曲面交于两个点
(
可能是重点或虚点
)
;
3. 平面
π
与二次曲面
Q
的交是一条二次曲线;
4. 在一般情况下,两个二次曲面的交是一条空间
4 次曲线。如果两个二次曲面都是锥面,则 它们的交线由两条二次曲线所构成。
5. 对于非退化的二次曲面
Q
上的每一点
X
都存在切平面
π
,切平面的坐标由
π
=Q
X 给出; 如果平面
π
是切平面,则切点
X 的坐标由
 给出。锥面 Q 在顶点处不存在切平面, 其他任何一点
X
都存在切平面
π
,切平面的坐标也由
π
=QX。与非退化二次曲面不同的是锥面同一条母线上的点有相同的切平面,也就是说给定锥面的切平面不能唯一确定它的切点。
给出。锥面 Q 在顶点处不存在切平面, 其他任何一点
X
都存在切平面
π
,切平面的坐标也由
π
=QX。与非退化二次曲面不同的是锥面同一条母线上的点有相同的切平面,也就是说给定锥面的切平面不能唯一确定它的切点。
给定一个二次曲面
Q
,则
π
=Q
X 确定了空间点与平面的的一个对应关系,通常称为由二次曲面
Q 的配极对应。如果二次曲面
Q 是非退化的,则它的配极对应是点与平面之间的一一对应。在几何上,如果点
X 在二次曲面
Q 上,则它的极平面是点
X 的切平面;如果点
X 不在(非退化)二次曲面
Q 上,则点
X 的极平面是以
X 为顶点的锥面与
Q 的切点所在的平面

在射影变换
X
′
=HX 下,二次曲面变换规则是:

空间曲面的对偶是指以该曲面的切平面为基本元素在对偶空间
(
面空间)中所构成的曲面,通常 称对偶曲面Q
*
。
在一般情况下,二次曲面的对偶仍为一个二次曲面。
Q
是
Q
*
中的所有平面所形成的包络
非退化二次曲面的对偶
Q
* 仍是二次曲面,并且
 。
。
锥面的对偶是一条平面曲线
锥面
Q 的对偶在对偶空间中是一条二次曲线,这条二次曲线的支撑面是锥面顶点的对偶,锥面
Q
的母线在对偶空间中被压缩为二次曲线上的一个点。锥面
Q 的对偶可以用下述方程来描述:


空间二次曲线的对偶曲面是一个锥面,二次曲线的支撑平面的对偶是这个锥面的顶点,二次曲线上的一个点在对偶空间中被扩展为锥面的一条母线,二次曲线的切线与锥面的母线构成一一对应关系。

对偶二次曲面的变换规则
在
(
点
)
变换
X
′
=H
X 下,应用平面的变换规则
 ,立即得到对偶二次曲面Q *的变换规则:
,立即得到对偶二次曲面Q *的变换规则:

锥面的对偶曲面
Q
* 是一条空间二次曲线,可以由对偶锥面和平面的变换规则来联合表达:

绝对二次曲线
绝对二次曲线
 是
是
 上的一条
(
点)二次曲线。在欧氏坐标系下
上的一条
(
点)二次曲线。在欧氏坐标系下
 ,
,

是下述方程的解集:

它是
 上的一条虚二次曲线。尽管
上的一条虚二次曲线。尽管
 没有实点,但它具有二次曲线的共同性质
没有实点,但它具有二次曲线的共同性质
性质:

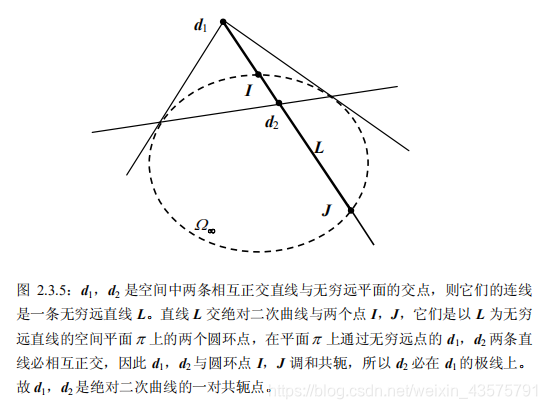
三维射影空间中,令
d
1
和
d
2
是两条直线与二次曲线
 所在平面
所在平面
 的交点,它表示这两条直线在射影空间中的方向。
的交点,它表示这两条直线在射影空间中的方向。
 是绝对二次曲线在平面
是绝对二次曲线在平面
 上的矩阵表示。则两条直线交角可以通过下述公式来计算:
上的矩阵表示。则两条直线交角可以通过下述公式来计算:

绝对二次曲线
 的对偶是三维空间中的退化对偶二次曲面,称它为绝对二次曲面并记为
的对偶是三维空间中的退化对偶二次曲面,称它为绝对二次曲面并记为
 。
。
在三维射影空间中,若绝对二次曲面的矩阵表示为
 ,则两平面
π
1
和
π
2 之间的夹角由下式给出:
,则两平面
π
1
和
π
2 之间的夹角由下式给出:

特别地,在欧氏空间中,若两平面的坐标
 ,则两平面的夹角计算公式简化为:
,则两平面的夹角计算公式简化为:

令
Q
r
是中心在原点半径 r 为的球面,则它的矩阵表示为

即球面
Qr 上的点
 满足方程:
满足方程:

可以将绝对二次曲线作为球面
Q
r
在
r
→ ∞ 时的极限。








 本文深入探讨三维射影变换的概念,包括变换矩阵、二次曲面的性质及变换规则,以及绝对二次曲线和曲面的特性。揭示了射影变换如何影响空间中的点、线、面和二次曲面。
本文深入探讨三维射影变换的概念,包括变换矩阵、二次曲面的性质及变换规则,以及绝对二次曲线和曲面的特性。揭示了射影变换如何影响空间中的点、线、面和二次曲面。
















 98
98

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








