Pytorch——momentum动量

一、Momentum：(动量，冲量)：结合当前梯度与上一次更新信息，用于当前更新；

二、Momentum的作用？

主要是在训练网络时，最开始会对网络进行权值初始化，但是这个初始化不可能是最合适的；因此可能就会出现损失函数在训练的过程中出现局部最小值的情况，而没有达到全局最优的状态。

momentum的出现可以在一定程度上解决这个问题。动量来源于物理学，当momentum越大时，转换为势能的能量就越大，就越有可能摆脱局部凹区域，从而进入全局凹区域。momentum主要是用于权值优化。

没引入momentum之前的权重更新：

上面的权重更新可以通过下图进行理解！

梯度下降法

 以单个参数w的损失函数L(w)为例，前提这个损失函数是可微的；

 

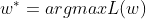
主要目的就是求解使得上述Loss的最小的，实际上就是寻找切线L斜率为0的全局最小值（这里可能会出现局部最小值，斜率也为0，也就引出了下面的momentum）

最简单的方法就是遍历所有的w的值，去找到使得loss最小的，但是这样做一点效率也没有；使用梯度下降法可以很好地解决这个问题；

1. 首先随机选取一个初始的点 (当然也不一定要随机选取，如果有办法可以得到比较接近 的表
   现得比较好的当初始点，可以有效地提高查找的效率)
2. 计算L在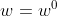的位置的微分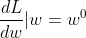， ，几何角度就是切线的斜率；
3. 如果切线斜率是negative负的，那么就应该使w变大，即往右踏一步；如果切线斜率是positive正
   的，那么就应该使w变小，即往左踏一步，每一步的步长step_size就是w的改变量
   w的改变量step_size的大小取决于两件事 

• 一是现在的微分值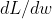有多大，微分值越大就表示所在位置比较陡峭，那么它将要移动的距离就越大，反之就越小；
• 二是一个常数项  ，其实就是学习率；它决定了每次踏出的step_size不仅取决于现在的斜率，还取决于提前设置好的学习率值，如果设置的学习率值比较大，那么每次踏出一步的时候，参数w更新的幅度就比较大，反之参数更新的幅度就比较小；学习也不能太大，太大可能会直接跳过全局最小值点；

     4.因此每次参数更新的大小是 ，为了满足斜率为负时w表大，斜率为正时w表小，应该使原来的w减去更新的数值，可以结合上图梯度下降法进行理解；即下式

 此时的对应的斜率为0，我们找到了一个局部最小值，但是一旦出现微分为0的情况，参数就不会再继续更新了，但是这个没办法满足全局最小值；这个情况可以结合下图进行理解；于是引出了增加momentum的方法；下面继续看增加momentum的情况；

上面是针对单一参数而言的，针对多个参数的情况也是和处理单个参数的问题一样的，这里就不多赘述了。

---

引入momentum之后：

其中表示权重，表示学习率，表示的导数，表示速度，一般初始化为0；就是引入的动量，一般是设置为0.9。可以理解为，如果上一次的  与当前的负梯度方向是相同的，那这次下降的幅度就会加大，从而可以加快模型收敛。

指数加权平均：参考：通俗理解指数加权平均

 

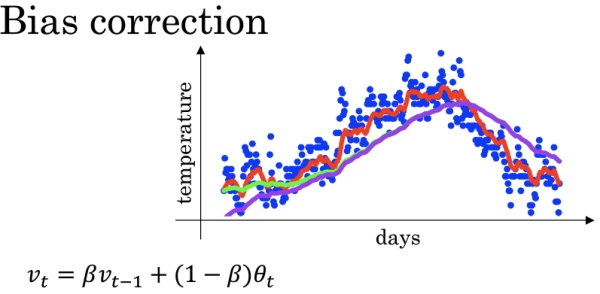
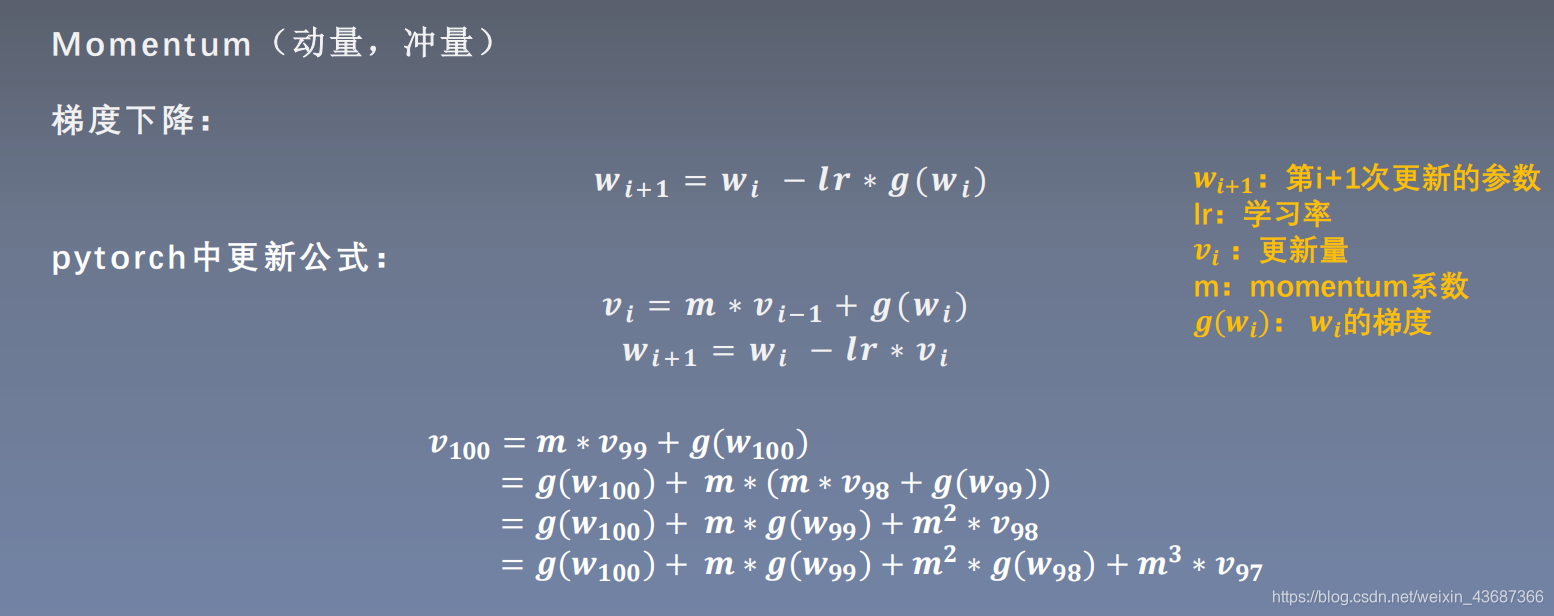
 通过代码进一步理解：

1、首先看一下指数加权平均

import torch
import numpy as np
import torch.optim as optim
import matplotlib.pyplot as plt
torch.manual_seed(1)

# 指数加权平均
def exp_w_func(beta,time_list):
    return [(1 - beta)*np.power(beta,exp) for exp in time_list]

beta = 0.9
num_point = 100
time_list = np.arange(num_point).tolist()

# 指数权重
weights = exp_w_func(beta,time_list)

plt.plot(time_list,weights,'-ro',label="Beta:{}\ny = B^t * (1-B)".format(beta))
plt.xlabel("time")
plt.ylabel("weight")
plt.legend()
plt.title("exponentially weighted average")
plt.show()
print(np.sum(weights))

0.9999734386011124

2、针对多个动量的情况

# multi weights
# 通常都是设置动量为0.9
beta_list = [0.98,0.95,0.9,0.8]
w_list = [exp_w_func(beta,time_list) for beta in beta_list]
for i,w in enumerate(w_list):
    plt.plot(time_list,w,label="Beta:{}".format(beta_list[i]))
    plt.xlabel("time")
    plt.ylabel("weight")
plt.legend()
plt.show()

3、optim.SGD中的momentum

# SGD中的momentum
def func(x):
    return torch.pow(2*x,2)  # y = (2x)^2 = 4*x^2   dy/dx = 8x

iteration = 100
m = 0.9
lr_list = [0.01,0.03]

momentum_list = list()
loss_rec = [[] for l in range(len(lr_list))]
iter_rec = list()

for i,lr in enumerate(lr_list):
    x = torch.tensor([2.],requires_grad=True)
    momentum = 0. if lr == 0.03 else m
    momentum_list.append(momentum)
    
    optimizer = optim.SGD([x],lr=lr,momentum=momentum)
    
    for iter in range(iteration):
        y = func(x)
        y.backward()
        optimizer.step()
        optimizer.zero_grad()
        loss_rec[i].append(y.item())
        
for i,loss_r in enumerate(loss_rec):
    plt.plot(range(len(loss_r)),loss_r,label="LR:{} M:{}".format(lr_list[i],momentum_list[i]))
plt.legend()
plt.xlabel("Iteration")
plt.ylabel('Loss value')
plt.show()

可以看出增加了动量的loss呈现波动，但是可以很快达到最小值，同样也会逐渐趋于平缓。