从理论到实践-卡尔曼滤波与行人目标追踪

卡尔曼滤波由来

根据根据贝叶斯滤波快速理解卡尔曼滤波Kalman Filter(KF)
这篇文章，我们理解了卡尔曼滤波的由来：

卡尔曼滤波公式

一维卡尔曼滤波

多维卡尔曼滤波

基于卡尔曼滤波的行人位置估算

确定状态表示方式

当我们要估计一个行人状态的时候，首先要建立要估计的状态的表示。
行人的状态大概可以表示为x = （P,V）；其中P为行人的位置，V为行人当前时刻的速度。
我们用向量坐标来表示这个状态就是：

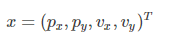
确定基于当前状态的处理模型（运动模型/预测模型/状态方程）

在确定了我们要估计的状态以后，我们需要确定一个处理模型，处理模型用于预测阶段来产生一个对当前估计的先验（预测）。本文中，我们研究的是KF（线性系统）.所以我们现已一个最简单地处理模型来标书行人的运动–恒定速度模型

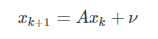
即：

之所以称之为恒定速度模型，是因为我们将上面这个行列式展开可以得到：

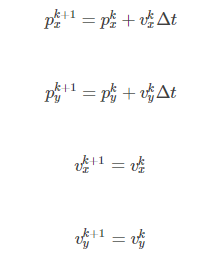
恒定速度处理模型假定预测的目标的运动规律是恒定的速度的，在行人状态预测这个问题中，很显然行人并不一定会以恒定的速度运动，所以我们的处理模型包含了一定的 处理噪声，在这个问题中处理噪声也被考虑了进来，其中的 V 是我们这个处理模型的处理噪声。在行人状态估计中的处理噪声其实就是行人的加减速，那么我们原来的处理过程就变成了：

根据状态方程计算预测误差协方差矩阵：

预测方程完整公式为：

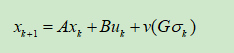
（其实此处的加速度既可以理解为内部控制量，也可以理解为过程噪声，对于这个模型来说，不会影响后续的计算。）

此处暂时把加速度矩阵理解为过程噪声矩阵把
我们的预测第二步就变成了：

A是预测误差协方差系数，系数和预测方程保持一致，但是方差是平方，所以是A的平方，因为矩阵相乘的特殊性，所以其中一个A转换成A的转置。Q是过程噪声协方差，（方差是平方）：

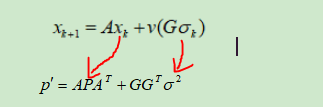
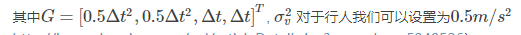
确定测量值缩放系数C

实际的传感器测量除了会有测量噪声 vk 以外，还会存在一定的关于真实状态的缩放，因此我们使用 xk 表示测量时通常还会在其前面加一个缩放系数 c。

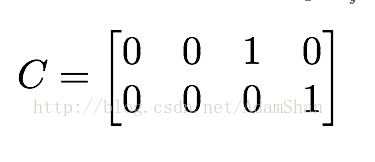
1代表无缩放；（测量值只有vx vy）

确定测量噪声协方差矩阵

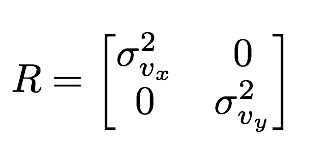
这是传感器固有的性质，所以往往是传感器厂商提供。

创建单位矩阵

python程序

#coding=utf-8
#---------------------------------------------------------------------------------------------------------------------------
#NumPy 通常与 SciPy（Scientific Python）和 Matplotlib（绘图库）一起使用， 
# 这种组合广泛用于替代 MatLab，是一个强大的科学计算环境，有助于我们通过 Python 学习数据科学或者机器学习。
#SciPy 是一个开源的 Python 算法库和数学工具包。
#SciPy 包含的模块有最优化、线性代数、积分、插值、特殊函数、快速傅里叶变换、信号处理和图像处理、常微分方程求解和其他科学与工程中常用的计算。
#Matplotlib 是 Python 编程语言及其数值数学扩展包 NumPy 的可视化操作界面。它为利用通用的图形用户界面工具包，
# 如 Tkinter, wxPython, Qt 或 GTK+ 向应用程序嵌入式绘图提供了应用程序接口（API）。

import numpy as np  
import matplotlib.pyplot as plt
from scipy.stats import norm  #正太分布密度函数有关的模块
#------------------------------------------------------------------------------------------------------------------------
#接着我们初始化行人状态x, 行人的不确定性（协方差矩阵）P，测量的时间间隔dt，处理矩阵F以及测量矩阵H
x = np.matrix([[0.0, 0.0, 0.0, 0.0]]).T#初始化行人的状态
print(x, x.shape)
P = np.diag([1000.0, 1000.0, 1000.0, 1000.0])#diag 初始化一个对角矩阵（协方差矩阵），行人的不确定性
print(P, P.shape)

dt = 0.1 # 确定时间步长
F = np.matrix([[1.0, 0.0, dt, 0.0],#处理矩阵F
              [0.0, 1.0, 0.0, dt],
              [0.0, 0.0, 1.0, 0.0],
              [0.0, 0.0, 0.0, 1.0]])
print(F, F.shape)

H = np.matrix([[0.0, 0.0, 1.0, 0.0],#初始化测量矩阵放大系数
              [0.0, 0.0, 0.0, 1.0]])
print(H, H.shape)


#-----------------------------------------------------------------------------------------------------------
#计算测量过程的噪声的协方差矩阵R和处理噪声（过程噪声）的协方差矩阵Q：
ra = 10.0**2#测量噪声协方差
R = np.matrix([[ra, 0.0],#初始化测量噪声协方差矩阵
              [0.0, ra]])
print(R, R.shape)

#ra = 0.09
#R = np.matrix([[ra, 0.0],
 #             [0.0, ra]])
#print(R, R.shape)


sv = 0.5#过程噪声
G = np.matrix([[0.5*dt**2],#G矩阵-过程噪声协方差系数
               [0.5*dt**2],
               [dt],
               [dt]])
Q = G*G.T*sv**2#过程噪声协方差矩阵
#SymPy是符号数学的Python库。它的目标是成为一个全功能的计算机代数系统，同时保持代码简洁、易于理解和扩展。
#Symbol 是一种基本数据类型
# Matrix矩阵运算库
from sympy import Symbol, Matrix
from sympy.interactive import printing
printing.init_printing() #根据环境选择输出方式
dts = Symbol('dt')#定义变量,此变量不是程序中认为的变量，而是数学公式里面的变量
Qs = Matrix([[0.5*dts**2],[0.5*dts**2],[dts],[dts]])
Qs*Qs.T
#-----------------------------------------------------------------------
# 初始化一个单位矩阵
I = np.eye(4)
print(I, I.shape)
#--------------------------------------------------------------------------------

m = 200 # 测量数
vx= 20 # in X
vy= 10 # in Y

mx = np.array(vx+np.random.randn(m))#生成200个X方向测量值
my = np.array(vy+np.random.randn(m))#生成200个Y方向测量值
measurements = np.vstack((mx,my))#生成二维矩阵

print(measurements.shape)
print('加速度测量的标准差=%.2f' % np.std(mx))
print('你假设 %.2f 在 R矩阵里.' % R[0,0])

fig = plt.figure(figsize=(16,5))#创建一个图片
plt.step(range(m),mx, label='$\dot x$')#step 阶梯图
plt.step(range(m),my, label='$\dot y$')
plt.ylabel(r'Velocity $m/s$')
plt.title('Measurements')
plt.legend(loc='best',prop={'size':18})#显示label
#---------------------------------------------------------------------------------

xt = []
yt = []
dxt= []
dyt= []
Zx = []
Zy = []
Px = []
Py = []
Pdx= []
Pdy= []
Rdx= []
Rdy= []
Kx = []
Ky = []
Kdx= []
Kdy= []

def savestates(x, Z, P, R, K):
    xt.append(float(x[0]))
    yt.append(float(x[1]))
    dxt.append(float(x[2]))
    dyt.append(float(x[3]))
    Zx.append(float(Z[0]))
    Zy.append(float(Z[1]))
    Px.append(float(P[0,0]))
    Py.append(float(P[1,1]))
    Pdx.append(float(P[2,2]))
    Pdy.append(float(P[3,3]))
    Rdx.append(float(R[0,0]))
    Rdy.append(float(R[1,1]))
    Kx.append(float(K[0,0]))
    Ky.append(float(K[1,0]))
    Kdx.append(float(K[2,0]))
    Kdy.append(float(K[3,0]))    

for n in range(len(measurements[0])):#循环200次

    # 时间更新（预测）
    # ========================
    # 预测未来状态
    x = F*x

    # 预测误差协方差
    P = F*P*F.T + Q

    # 测量更新
    # ===============================
    # 计算卡尔曼增益
    S = H*P*H.T + R
    K = (P*H.T) * np.linalg.pinv(S)#pinv计算广义逆矩阵

    # 通过Z更新估算值
    Z = measurements[:,n].reshape(2,1)#获取测量值
    y = Z - (H*x)                            # 决定最优值偏向测量值还是预测值
    x = x + (K*y)                           

    # 更新误差协方差矩阵
    P = (I - (K*H))*P

    # 为打点保存数据
    savestates(x, Z, P, R, K)

def plot_x():
    fig = plt.figure(figsize=(16,9))#--创建图片
    plt.step(range(len(measurements[0])),dxt, label='$estimateVx$')
    plt.step(range(len(measurements[0])),dyt, label='$estimateVy$')

    plt.step(range(len(measurements[0])),measurements[0], label='$measurementVx$')
    plt.step(range(len(measurements[0])),measurements[1], label='$measurementVy$')

    plt.axhline(vx, color='#999999', label='$trueVx$')
    plt.axhline(vy, color='#999999', label='$trueV                                              y$')

    plt.xlabel('Filter Step')
    plt.title('Estimate (Elements from State Vector $x$)')
    plt.legend(loc='best',prop={'size':11})
    plt.ylim([0, 30])
    plt.ylabel('Velocity')
plot_x()
plt.show()

C++程序

在这里插入代码片

结论

卡尔曼滤波存在着一个非常大的局限性——它仅能对线性的处理模型和测量模型进行精确的估计，在非线性的场景中并不能达到最优的估计效果，为了能够设定线性的环境，我们假定了我们的处理模型为恒定速度模型，但是显然在显示的应用中不是这样的，不论是处理模型还是测量模型，都是非线性的，下一篇学习一种能够应用于非线性情况的卡尔曼滤波算法——扩展卡尔曼滤