Taylor级数定义和常用的Taylor级数展开式

Taylor级数 是一种表达一个函数的无穷级数，它基于该函数在某点的导数信息。通过Taylor级数，我们可以近似计算某个函数在某一点附近的值。

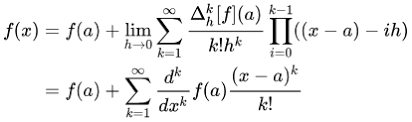
1. Taylor级数定义

假设函数 $f(x)$ 在点 $a$ 处具有任意阶导数（即 $f^{\prime }(a),f^{\prime \prime }(a),f^{(n)}(a)$ 存在）。则该函数在 $a$ 附近的Taylor级数展开为：

$$f(x)=f(a)+f^{\prime }(a)(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+\frac{f^{(3)}(a)}{3!}(x-a{)}^3+\cdots =\sum _{n=0}^{\infty }\frac{f^{(n)}(a)}{n!}(x-a{)}^n$$

其中：

• $f(a)$ 是函数在 $a$ 处的值，
• $f^{\prime }(a)$ 是函数在 $a$ 处的导数值，
• $f^{\prime \prime }(a)$ 是函数在 $a$ 处的二阶导数值，依此类推。

2. 推导过程

推导步骤：

1. 函数的定义：
   设 $f(x)$ 在点 $a$ 处具有足够高阶的导数。

2. 函数的增量：
   我们考虑函数 $f(x)$ 在点 $x$ 附近的增量，假设 $x=a+h$，其中 $h=x-a$，则：
   $$f(a+h)=f(a)+\Delta f=f(a)+f^{\prime }(a)h+\frac{f^{\prime \prime }(a)}{2!}{h}^2+\frac{f^{(3)}(a)}{3!}{h}^3+\dots$$
   这里 $\Delta f$ 是函数增量。

3. 高阶导数的贡献：
   如果我们继续对 $f(x)$ 进行高阶展开，可以得到更高阶的导数对增量的贡献。例如，二阶导数贡献为：
   $$\frac{f^{\prime \prime }(a)}{2!}{h}^2$$
   逐步将高阶导数加进来，得到无限级数。

4. 级数的形式：
   通过重复类似过程（逐项展开每一阶的导数），得到函数 $f(x)$ 在 $x$ 处的Taylor级数展开式：
   $$f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(a)}{n!}(x-a{)}^n$$
   其中每一项的系数是函数在 $a$ 处的导数值除以阶乘。

3. Taylor级数的收敛性

Taylor级数的收敛性（即该级数是否能够精确地表示函数）取决于函数本身及其在 $a$ 处的性质。对于某些函数，Taylor级数在 $a$ 附近的收敛半径是有限的，这意味着该级数只能在某个区间内近似函数；对于其他函数，Taylor级数可能在整个定义域内收敛。

例如，指数函数 $e^x$ 和正弦函数 $\sin (x)$ 在所有实数上都有无穷的收敛半径，因此它们的Taylor级数可以在全域内收敛并精确表示函数。

4. 常见的Taylor级数展开式

一些常见函数的Taylor级数展开如下：

• 指数函数 $e^x$ 在 $a=0$ 处的展开：
  $$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots =\sum _{n=0}^{\infty }\frac{x^n}{n!}$$

• 正弦函数 $\sin (x)$ 在 $a=0$ 处的展开：
  $$\sin (x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots =\sum _{n=0}^{\infty }(-1{)}^n\frac{x^{2n+1}}{(2n+1)!}$$

• 余弦函数 $\cos (x)$ 在 $a=0$ 处的展开：
  $$\cos (x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots =\sum _{n=0}^{\infty }(-1{)}^n\frac{x^{2n}}{(2n)!}$$

---

5. 结论

Taylor级数通过对函数的各阶导数进行展开，能够在给定点附近非常准确地逼近该函数。级数的展开能够在函数连续且具有足够高阶导数的情况下应用。对于一般的分析和计算问题，Taylor级数提供了一种强大的工具，用于近似计算复杂的函数值。