点与线段的关系

有一点P和线段AB，已知点P的坐标和线段两个端点（A点和B点）的坐标。

1. 求线段AP在线段AB上的投影长度；
2. 求点P在线段AB上的投影点的坐标；
3. 判断点P的投影点是否在线段AB内；
4. 求∠PAB的角度值；
5. 判断∠PAB是锐角、直角，还是钝角。

可以使用向量法求解以上问题。

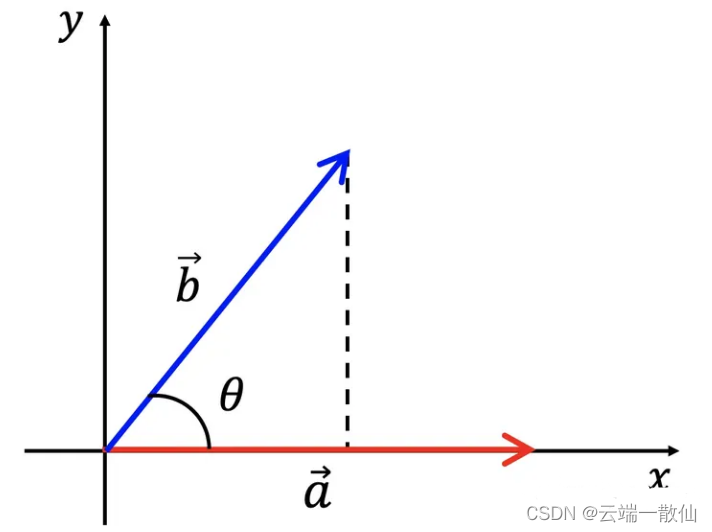
对于向量$\vec{a}(x_1,y_1)$，$\vec{b}(x_2,y_2)$，

• 点乘的公式为：$\vec{a}\cdot \vec{b}=x_1\cdot y_1+x_2\cdot y_2$，
• 点乘的几何意义为：$\vec{a}\cdot \vec{b}=|\vec{a}|\cdot |\vec{b}|cos\theta$

若把cos放到等式左侧，这个运算也可以理解为：在点乘运算中，b向量投影到a向量上（或a向量投影到b向量上，两者相同），然后通过除以它们的标量长度来“标准化”。这个值一定是小于等于1的，可以转化为一个角度值。

1. 即为计算向量b在向量a方向上的投影长度（有正负之分）；
2. 有了投影长度，除以向量a的标量长度，即得到点P的投影与线段AB的投影关系r；
   若 r < 0：点P的投影点在点A方向上的延长线上；
   若 r = 0：点P的投影点即为A点；
   若 0 < r < 1：点P的投影点在线段AB内；
   若 r = 1：点P的投影点即为B点；
   若 r > 1： 点P的投影点在点B方向上的延长线上。
3. 有了投影关系，再根据点A的坐标，即可求出点P投影点的坐标；
4. ∠PAB即为两个向量之间的夹角；
5. 判断∠PAB是锐角、直角，还是钝角，只需根据向量a和b的点乘结果来判断：
   若 > 0：向量a和b的方向相同，∠PAB是锐角；
   若 = 0：向量a和b正交，∠PAB是直角；
   若 < 0：向量a和b的方向相反，∠PAB是钝角。

向量的叉乘，又叫向量积、叉积。

向量a和向量b的叉积是一个向量，而不是一个标量。向量a和向量b的叉积是一个法向量：

1. 该向量垂直于向量a和b构成的平面，遵循右手定则。即将右手食指指向a的方向，中指指向b的方向，则此时拇指的方向即为法向量的方向。这一定则意味着叉积满足反交换律：a
   x b = - b x a。
2. 该向量的模长是向量a和b组成的平行四边形的面积。

根据向量叉乘的几何意义，则可以知道：

1. 向量叉乘的结果的模长，即为这两个向量组成的平行四边形的面积；
2. 如果叉乘的结果为0，则两个向量方向相同或相反，或它们任意一个的长度为0（而点乘的结果为0，则两个向量互相垂直）；
3. 判断点P在向量AB的左侧还是右侧，则可根据向量 ABxAP 的叉乘结果 r 来判断，根据右手定则：
   若 r > 0，则点P在向量AB的左侧；
   若 r = 0，则点P在向量AB上；
   若 r < 0，则点P在向量AB的右侧。