交流电机的电动势

导体中的电动势

首先,我们的目的是分析每根导体中的电动势大小,进而可以获得电枢的总电动势。而我们知道，导体电动势可以由如下公式求得：
$$\epsilon =Blv$$这个公式,想必大家高中就已经学过了,但是在大学里面,我们并不可以直接使用这个公式,而要考虑大量的实际情况,再加以使用。
既然有了目标公式,我们就知道下一步要做的事情了。那么看到这个公式，我们要思考的是，这里的磁场$B$是那一部分的磁场，以及$l$是什么，再一个就是$v$。

简单电机导体电动势

我们先从最简单的电机考虑,电机结构如下;

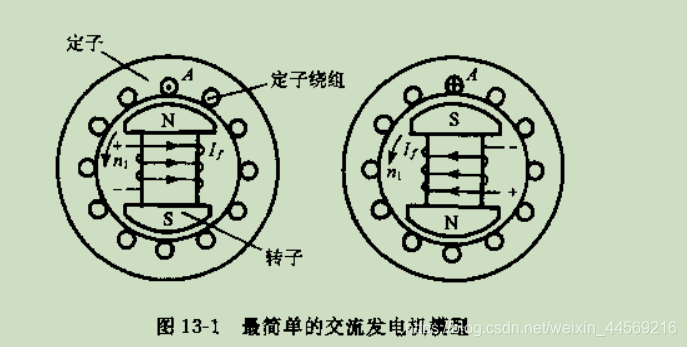
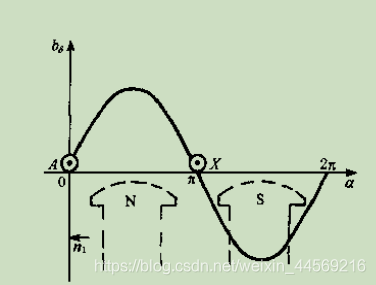
我们利用工具可以测出转子静止状态下,磁场$B$分布的实际情况(按照定子内圆周长$\alpha$的方向展开)为下图(b)中的$b_{\delta }$曲线.

我觉得啊,这个曲线极难用函数描述出来并加以分析,所以,使用了傅里叶级数将其分解成多个正弦函数,如下;
$$b_{\delta }=b_{\delta 1}+b_{\delta 3}+...+b_{\delta n}=B_{\delta 1}sin(\alpha )+B_{\delta 3}sin(3\alpha )+...+B_{\delta n}sin(n\alpha )$$通常,称$b_{\delta 1}$为基波分量,而$b_{\delta 3}$称为3次谐波分量,$b_{\delta 5}$为五次谐波分量,以此类推.

接下来,我们考虑第n次谐波分量下,导体A中感应电动势的瞬时值;
$$e_{An}=Blv=B_{\delta n}lvsin(n\alpha )=E_{n(max)}sin(nwt)=\sqrt{2}{E}_{n}sin(nwt)$$其中,$E_n$表示电动势的有效值.进一步计算其大小.
由于;
$$导体线速度;v=2\pi r\frac{n}{60}=2p\tau \frac{n}{60}=2\tau f_n$$其中$f_n$为导体中波产生的电动势频率

接下来,我们想要得到气隙每级谐波磁通量,用以化简公式,则;
$$\begin{gathered} 谐波气隙磁场平均值;B_{n(av)}=\frac{2}{\pi }{B}_{\delta n} \\ 气隙每级谐波磁通量;{\Phi }_n=B_{n(av)}l\tau \\ \tau 指的是定子内用长度表示的每级所占空间距离 \end{gathered}$$
利用上述参数计算$E_n$大小,
$$E_n=\frac{\sqrt{2}}{2}{B}_{\delta n}lv=\frac{\sqrt{2}}{2}\pi f_n{\Phi }_n=2.22f_n{\Phi }_n$$
由于,
$$f_n=\frac{nw}{2\pi }=nf$$
$f$为基波频率。
那么`，将每个所有分量产生的电动势相加即可得到导体内部的电动势。
如下，
$$e_A=e_{A1}+e_{A3}+...+E_{An}=2.22[{\Phi }_{1}sin(wt)+3{\Phi }_{3}sin(3wt)+...+n{\Phi }_{n}sin(nwt)]f$$
接下来计算整距线匝感应电动势.

由于单一整距线匝原件的两个元件边处在两个磁性相反的磁极下,因此,线匝两端有效电动势为;
$$E_A=2e_A$$
同样的，对应的N匝线圈感应电动势为；
$$E_A=2N{e}_A$$

(未完待续)