BUCK电路伏秒平衡（DCDC）

这是一个异步BUCK电路的拓扑图：

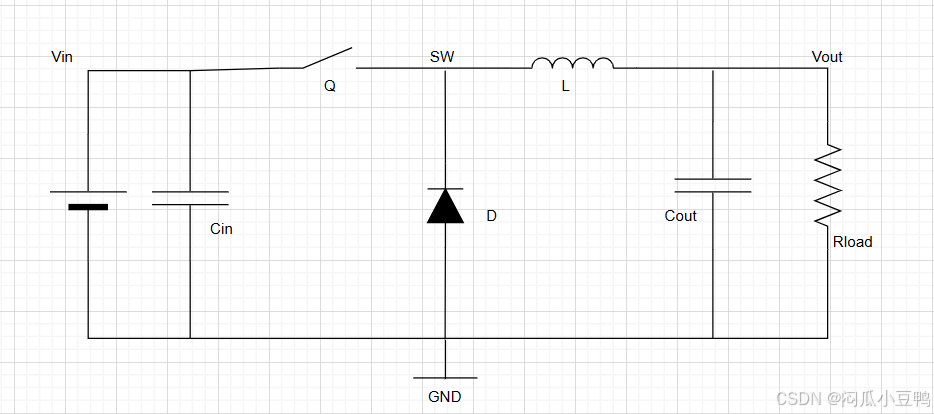
我们先来分析一下当开关Q闭合和断开时，电感的工作状态与电压：

• Q闭合时，输入电压Vin给负载Rload供电，同时给电感L充电，电感L处于充电状态，电感L两端的电压为：Vin-Vout；
• Q断开时， 电感L 给负载Rload 通过二极管D 供电， 电感L 处于放电状态，电感L 两端的电压为： -(Vout+Vd）；（注意：Vd为二极管两端的导通压降）

在 BUCK电路运行稳定后，‘Q闭合’和‘Q断开’时 ， 电感L两端的电压分别为 Vin-Vout 和 -(Vout+Vd），二者都是定值。
下面我们来看电感最重要的公式：

‘Q闭合’和‘Q断开’时，电感L的感值为定值不变，电感L两端的电压也是定值，保持不变；公式中U和L都是定值，则分别在 ‘Q闭合’ 和 ‘Q断开’ 时间段内时 di/dt 为常数，即在这两个时间段内，电感中的电流量是随着时间线性变化的；

由此，我们可以画出BUCK稳定时电感L中的电流随时间变化的图：

将上面的电感公式进行一个变形：

电感L的感值一定；
同时，因为负载电流恒定，一个周期内，开关Q导通时减小的电流大Δ i= 开关Q闭合时增加的电流Δ i；
所以：
Q导通时L两端的电压值 × 开关导通时间 = Q断开时L两端的电压值 × 开关断开时间（即伏秒平衡）

通过上面的式子，我们可以求出开关导通时间和开关断开时间，以及占空比：

由于我们使用异步BUCK进行推导，所以二极管的压降Vd无法忽略；当使用同步BUCK时，Vd看作0来处理即可；