多旋翼集群的分散时空轨迹规划

0 概览

分散结构的多旋翼机群具有灵活性和鲁棒性，而高效的时空轨迹规划仍然是一个挑战。该论文引入了分散式时空轨迹规划，将生成的质量良好的轨迹命名为$MINCO$应用到多智能体场景中。此方法确保了每个智能体在受群体协调或混乱环境中的安全要求的任何限制的情况下，进行高质量的局部规划。然后，将局部轨迹生成表示为一个无约束优化问题，可在毫秒内有效地求解。此外，还设计了一种分散的异步机制来触发每个智能体的局部规划。

0.1 算法

规划多旋翼集群，最关键的当然是规划算法了，研究群体规划的最底层需求，不仅可以将轨迹形状进行改变以避免碰撞，还可以调整时间剖面以开拓顺序解空间，进一步利用$agent$（智能体）的可行性，在时空联合轨迹优化是实现这个目标的主要算法，单个智能体在通过狭窄通道时往往会绕行等待其他的智能体，这会阻碍后面的智能体，并导致较差的解决方案。

---

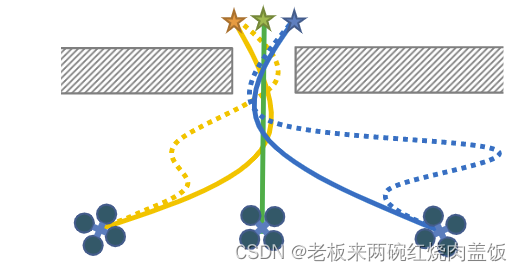
有/没有时间优化的轨迹比较。虚线曲线：没有时间优化，智能体使用弯路来延迟时间。实线曲线：通过时间优化，生成更短、更平滑的轨迹。

---

为此，采用了 Wang 等人最近开发的名为 $MINCO$ 的轨迹表示。 它专为积分链系统的时空轨迹优化而设计。

基于$MINCO$，提出了一种能够对空中群进行时空优化的分散式规划器。为了利用这种新颖的轨迹表示，设计了几个函数来惩罚碰撞、限制动态不可行性或规范轨迹持续时间（好像大体上思想与软约束的轨迹优化思想相关），使用 $MINCO$ 的梯度传播方案，典型多项式轨迹上的惩罚函数的梯度可以有效地传播到 $MINCO$ 的梯度。然后将规划问题表述为无约束优化，即使用定制的求解器在几毫秒内有效地求解。

0.2 架构

多旋翼集群的另一个基本要求是架构，它需要适度的相互依赖、稳健的通信机制和灵活的系统规模。高老师提出了一种分散和异步触发的规划策略，它可以减少问题的规模并将计算负担分配给每个智能体。

1 轨迹规划的相关工作

1.1 轨迹参数的优化

在传统方法中（类似$Minimum$ $Snap$，老朋友了，相关推导可以看这里），如下$(1)$式所示：
$$p_{\mu }(t)=\{\begin{array}{lc}{\sum }_{j=0}^N{\eta }_{1j}{\left(t-T_0\right)}^j& T_0\le t\le T_1\\ {\sum }_{j=0}^N{\eta }_{2j}{\left(t-T_1\right)}^j& T_1\le t\le T_2\\ ⋮& ⋮\\ {\sum }_{j=0}^N{\eta }_{Mj}{\left(t-T_{M-1}\right)}^j& T_{M-1}\le t\le T_M\end{array}(1)$$

大多是使用多项式曲线来作为决策变量，以及明确的连续性约束，轨迹分段是用添加中间路点这种方法，来变形分段多项式轨迹的。

航路点的分布，需要平衡一些可行性以及计算复杂度，为了优化多项式的时间分布，代表性方法使用具有数值差异的梯度下降法，然而，这种方法需要密集矩阵求逆来将航路点转换为系数，这就非常麻烦了。后来，通过使用$B\acute{e}zierCurve$以及$B-Spline$的共享凸包性质，更多的可以看这里，也就是曲线完全包含在其控制点的凸包当中的这个特性，使得问题简化了一些，这是因为这些曲线可以方便的添加约束，只需要把控制点限制在可行的凸包区域之内就可以了。但是吧，这种方法保守性因素偏多，可以有效防止轨迹在其物理特性极限的附近变得具有攻击性，对于贝塞尔曲线，其时间分布可以通过其基底进行调整，而对于$B-Spline$，其时间调整分布评估是高度非线性的，相当复杂，这种时间调整会导致曲折的轨迹形状。

之后，有了，$MINCO$，$MINCO$是一种新的轨迹表示，专门运用于集群的系统，$MINCO$的核心特点就是它在保持空间和时间最优性的同时有效地处理各种约束。可以通过离散化轨迹以添加约束，$MINCO$ 不像$B\acute{e}zierCurve$以及$B-Spline$那么保守，但在获得解决方案后需要进一步检查。尽管 $MINCO$ 是最复杂的表示并且需要复杂的实现，但它为无人机集群规划提供了坚实的基础。

1.2 $MINCO$

因为多旋翼的微分平坦度，其运动规划足以直接在时间可微的曲线上执行，$MINCO$是一个最小控制多项式轨迹，定义为如下$(2)$式：
T M I N C O = { p ( t ) : [ 0 , T ] ↦ R m ∣ c = M ( q , T ) q ∈ R m ( M − 1 ) , T ∈ R > 0 M } ( 2 ) \begin{gathered} \mathfrak{T}_{\mathrm{MINCO}}=\left\{p(t):[0, T] \mapsto \mathbb{R}^m \mid \mathbf{c}=\mathcal{M}(\mathbf{q}, \mathbf{T})\right. \\ \left.\mathbf{q} \in \mathbb{R}^{m(M-1)}, \mathbf{T} \in \mathbb{R}_{>0}^M\right\} \end{gathered} (2) TMINCO​={p(t):[0,T]↦Rm∣c=M(q,T)q∈Rm(M−1),T∈R>0M​}​(2)

$p(t)$是一个$m$维度的$M$段的多项式轨迹，阶数是$N=2s-1$，其中，$s$是相关积分链的阶数，$\mathbf{c}={\left({\mathbf{c}}_1^{\mathrm{T}},\dots ,{\mathbf{c}}_M^{\mathrm{T}}\right)}^{\mathrm{T}}\in {\mathbb{R}}^{2Ms\times m}$ ，CT是多项式的系数，就是上方的那个$p(t)$的多项式系数，$\mathbf{q}=\left({\mathrm{q}}_1,\dots ,{\mathrm{q}}_{M-1}\right)$ 则是中间航点（之前已经说过了，传统方法当中多项式分段是通过中间航点进行分段的），$\mathbf{T}={\left(T_1,T_2,\dots ,T_M\right)}^{\mathrm{T}}$ 则是分配给每一段轨迹的时间，综上，一个轨迹可以表示成$(3)$式这样：
$$p(t)=p_i\left(t-t_{i-1}\right),\forall t\in \left[t_{i-1},t_i\right](3)$$
第$i$段轨迹则是如$(4)$式所示：
$$p_i(t)={\mathbf{c}}_i^{\mathrm{T}}\beta (t),\forall t\in \left[0,T_i\right](4)$$

其中$\beta (t):={\left[1,t,\cdots ,t^N\right]}^{\mathrm{T}}$ 是自然基底（多项式的），${\mathbf{c}}_i\in {\mathbb{R}}^{2s\times m}$ 则是系数矩阵，$T_i=t_i-t_{i-1}$ 且 $T={\sum }_{i=1}^M{T}_i$。${\mathfrak{T}}_{\mathrm{MINCO}}$的核心就是根据构造参数映射$\mathbf{c}=\mathcal{M}(\mathbf{q},\mathbf{T})$ 来实现的。从技术上讲，该映射直接为任何指定的初始和终止条件的 $m$ 维 $s$ 积分器链构造最小控制轨迹。

---

• 这是$MINCO$的一个实例
  
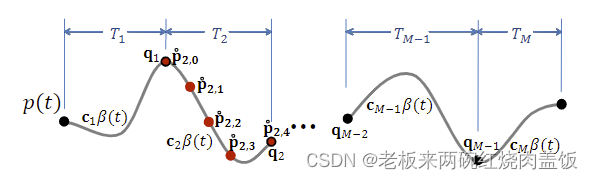
• 这个图说明了$MINCO$轨迹表示的参数以及其约束性，这个轨迹是由每个航点（中间路点$qi$和每段轨迹的时间参数$Ti$直接参数化的，红点，上方带个空心圆的符号$p$是约束点）

---

特征一： ${\mathfrak{T}}_{\text{MINCO }}$ 是满足以下最小控制力的多项式轨迹
$$\begin{array}{ll}{\min }_{p(t)}& {\int }_{t_0}^{t_M}{p}^{(s)}(t{)}^{\mathrm{T}}\mathbf{W}{p}^{(s)}(t)\mathrm{d}t,\\ \text{ s.t. }& p^{[s-1]}\left(t_0\right)={\bar{p}}_o,p^{[s-1]}\left(t_M\right)={\bar{p}}_f,\\ & p\left(t_i\right)=q_i,1\le i<M,\\ & t_{i-1}<t_i,1\le i\le M,\end{array}(5)$$
$\mathbf{W}\in {\mathbb{R}}^{m\times m}$ 是一个正项的对角矩阵，${\bar{p}}_o\in {\mathbb{R}}^{ms}$ 和 ${\bar{p}}_f\in {\mathbb{R}}^{ms}$ 是指定的初始和终止条件， $q_i\in {\mathbb{R}}^m$ 是轨迹在时间 $t_i$ 强制通过给定的中间路点，上方已经说过。

特征二： 关于之前的映射$\mathbf{c}=\mathcal{M}(\mathbf{q},\mathbf{T})$ ，其具体的对应关系可如下式
$$\mathbf{M}(\mathbf{T})\mathbf{c}=\mathbf{b}(\mathbf{q})(6)$$
其中 $\mathbf{M}(\mathbf{T})\in {\mathbb{R}}^{2Ms\times 2Ms}$ 是一个对于任何 $\mathbf{T}\succ 0$ 都具有非奇异特性的矩阵， $\mathbf{b}(\mathbf{q})\in {\mathbb{R}}^{2Ms\times m}$。 $(\mathbf{c},\mathbf{T})$ 和 $(\mathbf{q},\mathbf{T})$ 是使用具有 $O(M)$ 线性时间和空间复杂度的带状PLU分解来实现的，生成速度很快，在普通$CPU$上生成最小抖动轨迹大概需要 $1\mu s$。

特征三： 允许任何用户定义的目标函数或罚函数$F(\mathbf{c},\mathbf{T})$ ，$MINCO$对应的目标函数由下式$(7)$计算

$$H(\mathbf{q},\mathbf{T})=F(\mathcal{M}(\mathbf{q},\mathbf{T}),\mathbf{T})(7)$$

映射$\mathrm{c}=\mathcal{M}(\mathbf{q},\mathbf{T})$ 给出了一种线性复杂度方法，可以从相应的 $\partial F/\partial \mathbf{c}$ 和$\partial F/\partial \mathbf{T}$ 计算$\partial H/\partial \mathrm{q}$ 和$\partial H/\partial \mathbf{T}$。之后，高级优化器能够有效地优化目标。

1.3 时间积分约束

各种约束的实现方式与轨迹参数化方法密切相关。传统上，动态可行性和避免碰撞的要求被公式化为函数类型约束$\mathcal{G}\left(p(t),\dots ,p^{(s)}(t)\right)⪯0,\forall t\in [0,T]$。然而，这个公式不能直接通过约束优化来处理，因为 $\mathcal{G}$ 包含无限多的不等式约束。因此，我们通过约束违反积分将 $\mathcal{G}$ 转换为有限维。实际上，积分被转换为采样惩罚函数的加权和 $J_{\Sigma }(\mathbf{c},\mathbf{T})$。在大多数情况下，约束是解耦的，即$t_i\le t<t_{i+1}$ 的约束 $\mathcal{G}\left(p^{[s]}(t)\right)$仅由 ${\mathbf{c}}_i$ 和 $T_i$确定，第 $i$ 个轨迹片段的惩罚计算为
$$J_i\left({\mathbf{c}}_i,T_i,{\kappa }_i\right)=\frac{T_i}{{\kappa }_i}\sum _{j=0}^{{\kappa }_i}{\bar{\omega }}_j{\chi }^{\mathrm{T}}\max {\left(\mathcal{G}\left({\mathbf{c}}_i,T_i,\frac{j}{{\kappa }_i}\right),0\right)}^3(8)$$
其中 ${\kappa }_i$ 是第 $i$ 块上的样本数， $\chi \in {\mathbb{R}}_{\ge 0}^{n_g}$ 具有适当大条目的惩罚权重向量， $\left({\bar{\omega }}_0,{\bar{\omega }}_1,\dots ,{\bar{\omega }}_{{\kappa }_i-1},{\bar{\omega }}_{{\kappa }_i}\right)=(1/2,1,\cdots ,1,1/2)$ 是遵循梯形规则的正交系数。我们将由 { c i , T i , j / κ i } \left\{\mathbf{c}_i, T_i, j / \kappa_i\right\} {ci​,Ti​,j/κi​} 确定的点定义为约束点${\stackrel{\circ }{\mathrm{p}}}_{i,j}=p_i\left(\left(j/{\kappa }_i\right)T_i\right)$，其中 $p_i(t)$ 是第 $i$ 个多项式片段。那么 $\mathcal{G}\left({\mathbf{c}}_i,T_i,j/{\kappa }_i\right)=\mathcal{G}\left({\stackrel{\circ }{\mathrm{p}}}_{i,j}\right)$。注意 ${\stackrel{\circ }{\mathrm{p}}}_{i,{\kappa }_i}=$ ${\stackrel{\circ }{\mathrm{p}}}_{i+1,0}$，这里使用三次惩罚是因为它的两次连续可微性（注意看式$(8)$的三次方）。 $J_{\Sigma }(\mathbf{c},\mathbf{T})$ 被定义为总和：
$$J_{\Sigma }(\mathbf{c},\mathbf{T})=\sum _{i=1}^M{J}_i\left({\mathbf{c}}_i,T_i,{\kappa }_i\right)(9)$$
由于梯度，(c, $\mathbf{T})$ 由 $\left({\mathbf{c}}_i,{\mathbf{T}}_i\right)$ 构成，只使用链式法则给 ${\mathbf{c}}_i$ 和 $T_i$ 赋予梯度模板：

$$\begin{array}{c}\frac{\partial J_{\Sigma }}{\partial {\mathbf{c}}_i}=\frac{\partial J_{\Sigma }}{\partial \mathcal{G}}\frac{\partial \mathcal{G}}{\partial {\mathbf{c}}_i}\\ \frac{\partial J_{\Sigma }}{\partial T_i}=\frac{J_i}{T_i}+\frac{\partial J_{\Sigma }}{\partial \mathcal{G}}\frac{\partial \mathcal{G}}{\partial t}\frac{\partial t}{\partial T_i}\\ \frac{\partial J_{\Sigma }}{\partial \mathcal{G}}=3\frac{T_i}{{\kappa }_i}\sum _{j=0}^{{\kappa }_i}{\bar{\omega }}_j\max {\left(\mathcal{G}\left({\mathbf{c}}_i,T_i,\frac{j}{{\kappa }_i}\right),0\right)}^2\circ \chi \\ \frac{\partial t}{\partial T_i}=\frac{j}{{\kappa }_i},t=\frac{j}{{\kappa }_i}{T}_i\end{array}(10)$$

从上面的方程式$(10)$中，一旦约束 $\mathcal{G}$ 相对于多项式系数 ${\mathbf{c}}_i$ 和时间 $t$ 的梯度被评估，$J_{\Sigma }(\mathbf{c},\mathbf{T})$ 的梯度就被有效地计算了。

1.4 优化问题的构造

根据上述轨迹参数化和约束施加的定义，在本节中介绍了轨迹规划的完整优化。对期望轨迹的基本要求是平滑性、动态可行性以及障碍物和其他代理之间的安全性，还需要额外的目标，例如最小化控制工作和执行时间。采用 TMINCO 来解决最重要的问题。由于自然保证 $MINCO$ 是平滑的，因此无需在轨迹连续性上付出额外的努力（即顺滑性约束已经实现）。将轨迹生成公式化为一个无约束的优化问题：

$$\underset{\mathbf{q},\mathbf{T}}{\min }\sum _x{\lambda }_x{J}_x(11)$$
其中 $J_x$ 是 $J_{\Sigma }$ 的实例，${\lambda }_x$ 是目标或惩罚的权重，下标 x = { e , t , d , o , w , u } x=\{e, t, d, o, w, u\} x={e,t,d,o,w,u} 表示控制力 $(e)$、执行时间 $(t)$、动态可行性 $(d)$、避障 $(o)$、群体互惠避让$(w)$、约束点均匀分布$(u)$。通常，足够大的权重就足以进行处罚。该问题通过无约束非线性优化来解决。

1. 控制力 $J_e$：控制力遵循方程式中的定义。不失一般性，考虑第 $i$ 个片段 $p_i(t)$的单一维度：$p_i(t):\left[0,T_i\right]\mapsto \mathbb{R}$ 的多项式样条，其关于 ${\mathbf{c}}_i$ 和 $T_i$ 的导数是：
   $$\begin{array}{c}\frac{\partial J_e}{\partial {\mathbf{c}}_i}=2\left({\int }_0^{T_i}{\beta }^{(s)}(t){\beta }^{(s)}(t{)}^{\mathrm{T}}dt\right){\mathbf{c}}_i,\\ \frac{\partial J_e}{\partial T_i}={\mathbf{c}}_i^{\mathrm{T}}{\beta }^{(s)}\left(T_i\right){\beta }^{(s)}{\left(T_i\right)}^{\mathrm{T}}{\mathbf{c}}_i.\end{array}(12)$$

2. 执行时间$J_t:$ 更短的执行时间是可取的，因此也最小化加权总执行时间 $J_t=$ ${\sum }_{i=1}^M{T}_i$。显然，它的梯度$\partial J_t/\partial \mathbf{c}=0,\partial J_t/\partial \mathbf{T}=1$。

3. 动态可行性惩罚$J_d$：对于多旋翼飞行器的轨迹生成，动态可行性始终通过限制轨迹的导数来保证。在我们的工作中，我们限制了速度、加速度和加加速度的幅度。注意，动态可行性损失是使用秒中的时间积分获得的。速度、加速度和加加速度的约束表示为：

$${\mathcal{G}}_v=\dot{p}(t{)}^2-v_m^2,{\mathcal{G}}_a=\ddot{p}(t{)}^2-a_m^2,{\mathcal{G}}_j=p^{(3)}(t{)}^2-j_m^2(13)$$

其中 $v_m,a_m,j_m$ 是最大允许速度、加速度和加加速度。对应的梯度是

$$\frac{\partial {\mathcal{G}}_x}{\partial {\mathbf{c}}_i}=2{\beta }^{(n)}(t)p^{(n)}(t{)}^{\mathrm{T}},\frac{\partial {\mathcal{G}}_x}{\partial t}=2{\beta }^{(n+1)}(t{)}^{\mathrm{T}}{\mathbf{c}}_i{p}^{(n)}(t)(14)$$

其中 x = { v , a , j } , n = { 1 , 2 , 3 } x=\{v, a, j\}, n=\{1,2,3\} x={v,a,j},n={1,2,3}，$t=j{T}_i/{\kappa }_i+t_{i-1},t\in$ $\left[t_{i-1},t_i\right]$，代入方程式。得到罚分和 ${\mathbf{c}}_i$ 和 ${\mathbf{T}}_i$。再通过无约束非线性优化求解。

2 总结

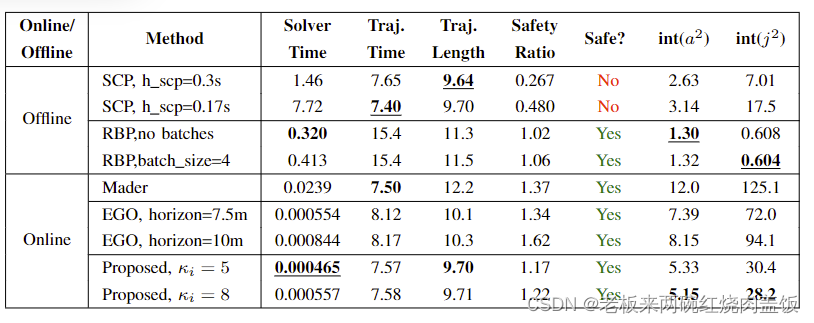
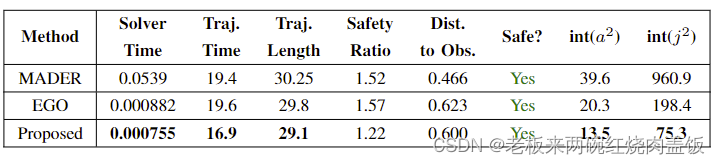
在包含 $8$ 个半径为 $0.25m$ 的智能体的 $8\times 8m$ 空白空间中进行比较。最大速度和加速度设置为 $1.7m/s$ 和 $6m/s^2$。安全比是最小代理间隔除以半径的两倍。$int(a^2)$ 和 $int(j^2)$ 是平方加速度和加加速度的时间积分，表示平滑度和控制，时间和距离的单位是秒和米。

---

---

---

在这项工作中，为多旋翼机群提出了一个分散的时空轨迹规划框架。这个框架由能够进行时空变形的 $MINCO$ 轨迹类和基于约束转录的时间积分惩罚函数提供支，所有这些组件都享有源自低复杂性的效率，执行广泛的基准测试以显示数量级的加速和顶级解决方案质量，真实的实验也证明了我们框架的广泛适用性。值得注意的是，也使规划者能够避免移动障碍物。由于使用不合作的群体，因此从规划者的角度来看，其他智能体和移动障碍物的行为相同。然而，由于运动物体检测和预测的前端不成熟，在当前工作中排除了这个模块，这被认为是未来在动态环境中实现完全自主的空中集群的工作。