编者
轨迹增长模型(Latent Class Trajectory Model,LCTM)又叫潜类别轨迹模型,它分为潜类别混合增长模型(LGMM/GMM)和群组轨迹模型(GBTM)(群组轨迹模型又叫组基轨迹模型,也可以称为潜类别增长模型(LCGA))。
轨迹增长模型近年来非常热门,今天这篇文章和诸位分享一下,干货多多!
本篇是潜变量系列文章第7篇
轨迹增长模型是近两年非常热门的纵向数据分析方法,那么在进入主题之前,我先简要介绍一下纵向数据。
拓展
纵向数据通俗点就是指是指对同一组受试个体或者受试单元在不同时间点上重复观测若干次,得到由截面和时间序列融合在一起的数据。
传统的纵向数据分析方法有:重复测量方差分析(RM-ANOVA)、广义估计方程(GEE)、线性混合效应模型(LMM)、广义线性混合效应模型(GLMM)、非线性混合效应模型(NONMEM)、潜增长曲线模型(LGCM)等等。
目前大多数纵向研究都使用线性混合效应模型(LMMs),该模型将重复测量与随机效应相关联,但其侧重于平均人口轨迹,没有考虑到某些个体在群体具有不同发展轨迹的可能性。而潜增长曲线模型是基于结构方程提出来的模型,用于探索群体特征随时间变化发展的过程或者轨迹,但是这一方法前提假设也是群体同质性。
传统的纵向数据分析方法都是不考虑异质性,认为所有的人都有同样的轨迹,协变量对所有人的作用都是一样的。但是这个假设往往不能总是成立,特别是以人为研究中心,人群中就算是同一个变量(特质)也是存在着不同的轨迹的,总体往往具有较大的异质性,所以如果我们用传统方法认为一个轨迹就能说明所有的问题的话,其实是过分简单化了,这时候我们就要考虑轨迹的潜类别了,这就涉及到了我们今天要讲的轨迹增长模型。
关于轨迹增长模型,我们要先了解一下它和传统纵向数据分析方法的区别。同一组数据,如果用传统的纵向分析方法做,也就是要假设群体有共同的发展参数 ,得到的总体发展轨迹就只有一条轨迹;而我们的轨迹模型分析,他是根据群体内个体的不同变化趋势,可以进一步的细化分析,概括成多个不同的水平,像我们图里分成了三组水平,就有了三个轨迹。

接下来我们看一下轨迹增长模型的具体定义。轨迹增长模型分为潜类别混合增长模型和群组轨迹模型。二者都是在给定的群体中,根据随时间发展的不同变化趋势将其分成不同的类(亚组),而区别就在于:
群组轨迹模型区别成不同的类之后,假设同一类中个体之间是相同的;
潜类别混合增长模型则考虑到了同一类别个体间的差异,它引入了随机效应来捕捉类别内的异质性。

我们进一步简单了解一下潜类别混合增长模型。
左边是全体个案的增长轨迹,传统方法模型试图去描述整个群体的增长情况,认为所有个体的增长情况都可以用一个轨迹去描述(左图中的实线)。
但是当我们提取出整个人群中的其中一个亚组人群(右图),其实这个亚组的增长趋势是和人群总体大不相同的,人群的总体趋势是在上升,此亚组则是在下降。
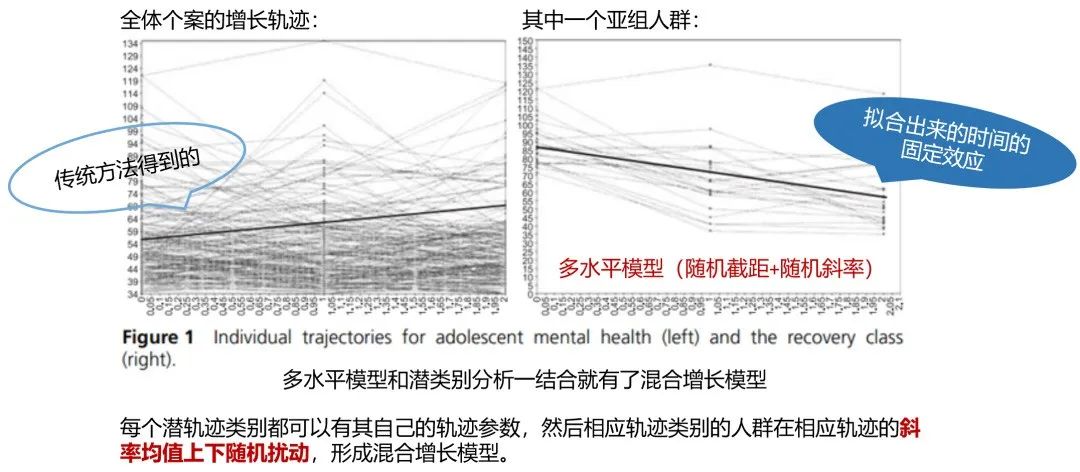
这两张图能够更明显的看出传统方法的弊端,这也是从一个侧面说明考虑轨迹的潜类别的重要意义。轨迹模型会把整个群体分为不同的亚组,潜类别混合增长模型认为,亚组内也是存在异质性的,每个潜轨迹类别都可以有其自己的轨迹参数,然后这个轨迹类别的人群在它轨迹的斜率均值上下随机扰动,形成增长混合模型。右图中间的实线是拟合出来这个亚组人群的时间的固定效应,而且这些亚组的斜率和截距也是不一样的。所以右图我们可以看成是一个多水平模型:由随机截距+随机斜率组成。
相比于潜类别混合增长模型,群组轨迹模型更常用些。群组轨迹模型是Nagin于1999年提出并将其定义为:有限混合模型的应用,使轨迹组作为统计工具,用于近似人口成员的未知轨迹。
接下来我们通过一篇文章深入地了解一下群组轨迹模型。
本公众号回复“沙龙”即可获得代码,PPT,数据等资料 |
案例分享
2020年9月,学者在《Alzheimers Research & Therapy》(一区,IF=9.0)发表题为:"Associations between social and intellectual activities with cognitive trajectories in Chinese middle-aged and older adults: a nationally representative cohort study" 的研究论文。

一、研究设计
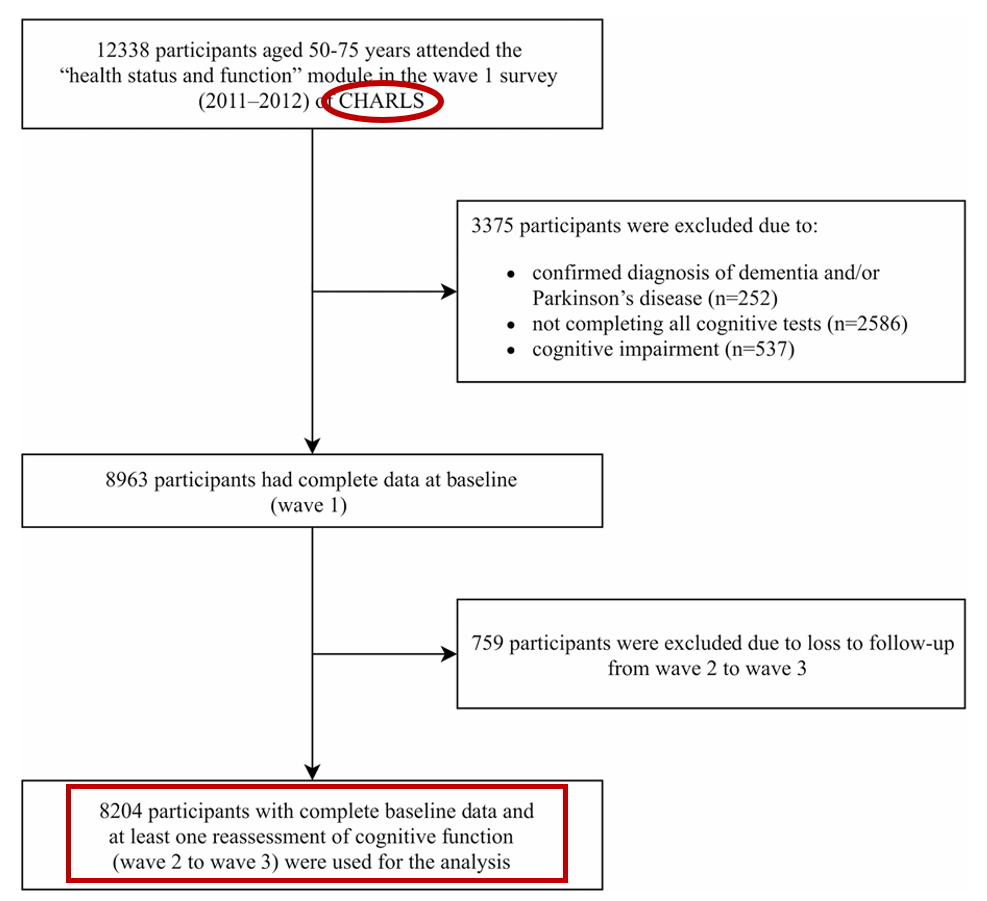
P(Population)研究对象:2011年-2016年(wave1~3)中国健康与养老追踪调查(CHARLS)参与者
E(Exposure)暴露:社交和智力活动:评估过去一个月的四项社交活动(与朋友互动;跳舞,锻炼或练习气功;参加社区相关组织;做志愿慈善工作或帮助他人)和四项智力活动(打麻将,纸牌或国际象棋;参加教育或培训课程;投资股票;和上网)。按照频率分为从不(分数 = 0)、不定期(分数 = 1)、几乎每周(分数 = 2)或几乎每天(分数 = 3)。社交和智力活动的总分范围为 0 到 12 分,分为 0、1-2 和≥ 3 。
C(covariant)协变量:年龄、性别、教育水平、婚姻状况、居住地点、家庭收入水平、吸烟、饮酒、自我报告的健康、医生诊断的慢性病、限制、自我报告的视觉和听力障碍、抑郁症状和体重指数 (BMI) 的基线测量值作为协变量纳入当前分析。
O(Outcome)结局:
主要结局:整体认知评分的轨迹:整体认知得分计算为情景记忆和心理完整性得分的总和,范围从 0 到 21;
次要结局:情景记忆和心理完整性评分的轨迹:单词回忆测试评估情景记忆,情景记忆分数计算为即时和延迟单词回忆的平均次数,范围从 0 到 10。认知功能电话访谈 (TICS)用于评估心理完整性,范围从0到11。
S(Study design)研究类型:队列研究。
二、统计学方法
1.使用一个对年龄、性别和教育程度进行调整的多元回归方程以获得预测的认知分数,然后用方程计算调整后的Z得分。我们使用这种方法来转换全局认知分数和单个认知领域的分数。转换后的Z分数用于分析。

2.使用群组轨迹模型(GBTM)拟合认知轨迹,并根据贝叶斯信息准则 (BIC) 和赤池信息准则(AIC)确定最佳拟合模型。


3.采用多项式logistic回归模型估计社会和智力活动与认知功能测量轨迹的关联

4.交互作用
在不同的模型中,还按年龄组(< 65 岁和 ≥ 65 岁)和性别(男性和女性)进行关联分析。通过在完全调整的模型中添加乘法交互项(即社会活动得分×性别)来测试效果修改。

三、主要结果
1.基线特征:
8204名受试者的平均年龄分别为60.09岁±6.37岁;52.3%的参与者是男性。在样本中,22.2%的参与者的社交活动得分≥3,7.4%的参与者的智力活动得分≥3。
2.估计的认知衰老轨迹:
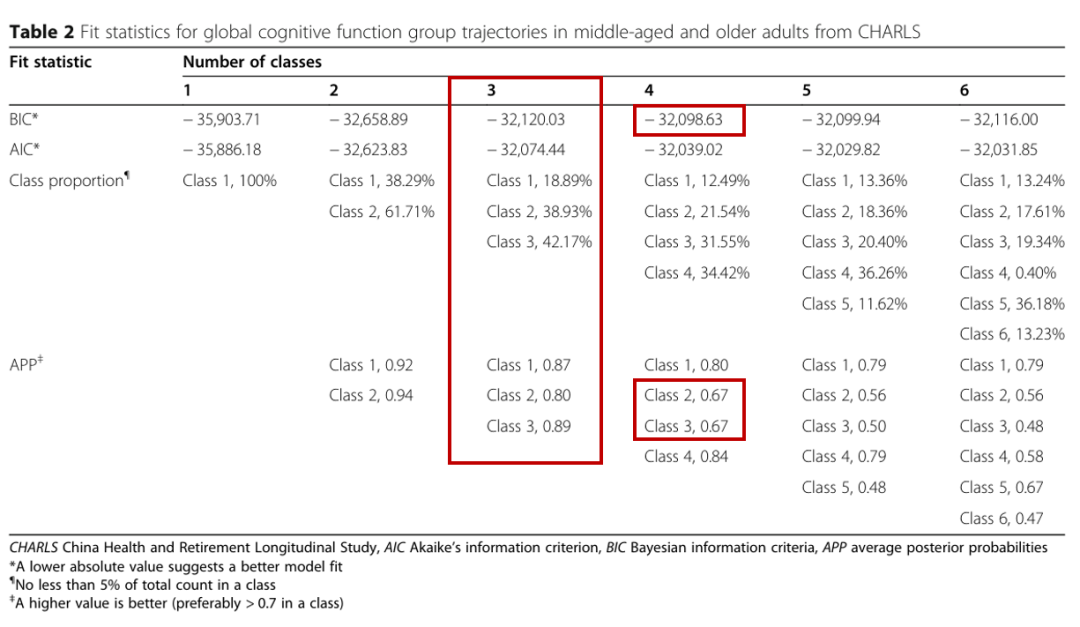
我们测试了认知功能的最佳轨迹,以解释该人群中整体认知评分的异质性(表2)。该模型的BIC最低,有四条轨迹(BIC = − 32,098.63);然而,两个轨迹组的平均后验概率小于 0.7。因此,我们确定了具有三个轨迹的GBTM模型作为最优模型。图 2 显示了认知功能的三种纵向模式,根据全球认知评分,按当前年龄绘制,每次就诊时:1 级,“持续低”(n = 1550,18.9%);第 2 类,“持续中度”(n = 3194,38.9%);第 3 类,“持续高”(n = 3460,42.2%)。表3总结了最终三组轨迹模型的最大似然估计值。认知功能域的三个群体轨迹如图3所示。

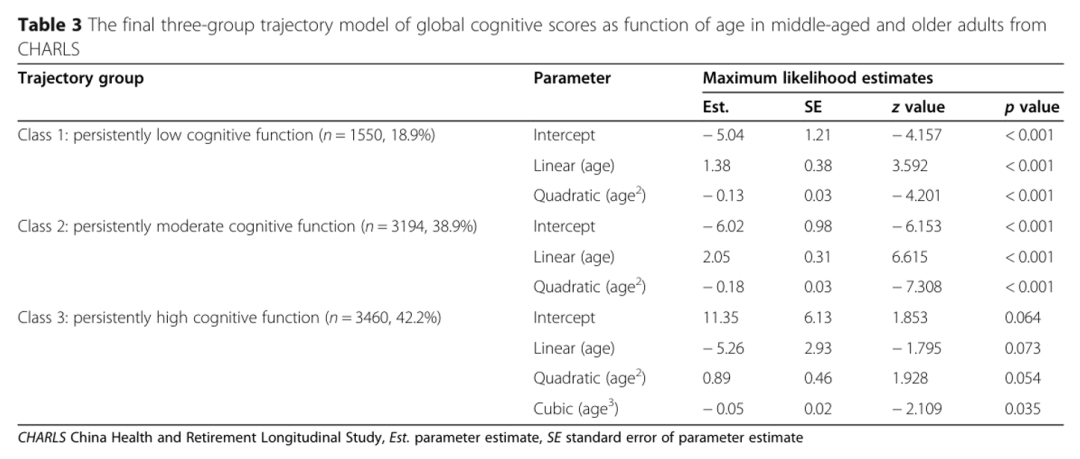

3.轨迹亚群基线特征:
表 4 列出了每个轨迹组中参与者的整体认知功能基线特征。与“持续高”轨迹组相比,“持续低”轨迹组的参与者更有可能年龄较大,女性,教育和收入水平较低,抑郁症状、限制日常潜水活动以及视力或听力障碍的患病率较高。

4.基线智力、社会活动评分和认知轨迹:
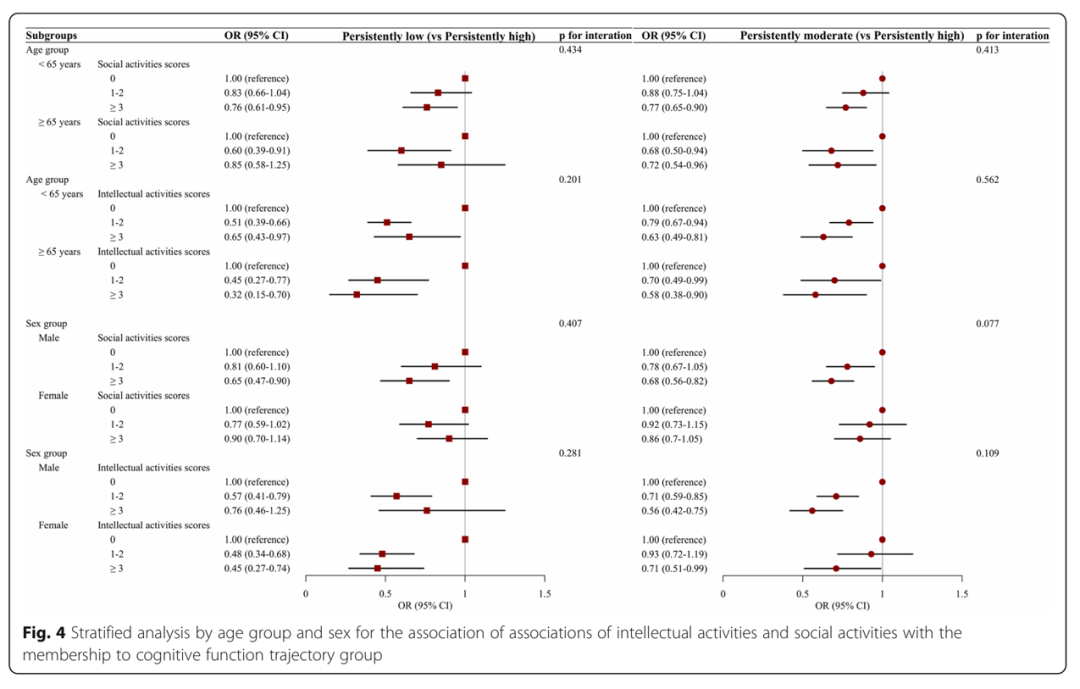
表 5 总结了多项式回归的结果,该回归检查了与认知轨迹成员相关的智力、社会活动分数。与未参加社交活动的参与者(得分=0)相比,报告经常参加社交活动(得分≥3)的成年人具有更好的认知轨迹,整体认知功能的“持续低”和“持续中度”轨迹的多变量调整OR(95%CI)分别为0.79(0.65-0.95)和0.76(0.66-0.87)。频繁参与智力活动(得分≥ 3)的相应OR(95%CI)为“持续低”认知功能为0.54(0.38-0.77),“持续中度”认知功能为0.62(0.50-0.77)。如图4所示,年轻(<65岁)和老年人(≥65岁)以及男性和女性(交互作用的p值均>0.05)之间,社会/智力活动与认知轨迹组的关联相似。
总结
1.群组轨迹模型/组基轨迹模型(GBTM)的用途与适用性

2.群组轨迹模型/组基轨迹模型(GBTM)的建模过程

3.群组轨迹模型/组基轨迹模型(GBTM)的拟合选择与评价指标
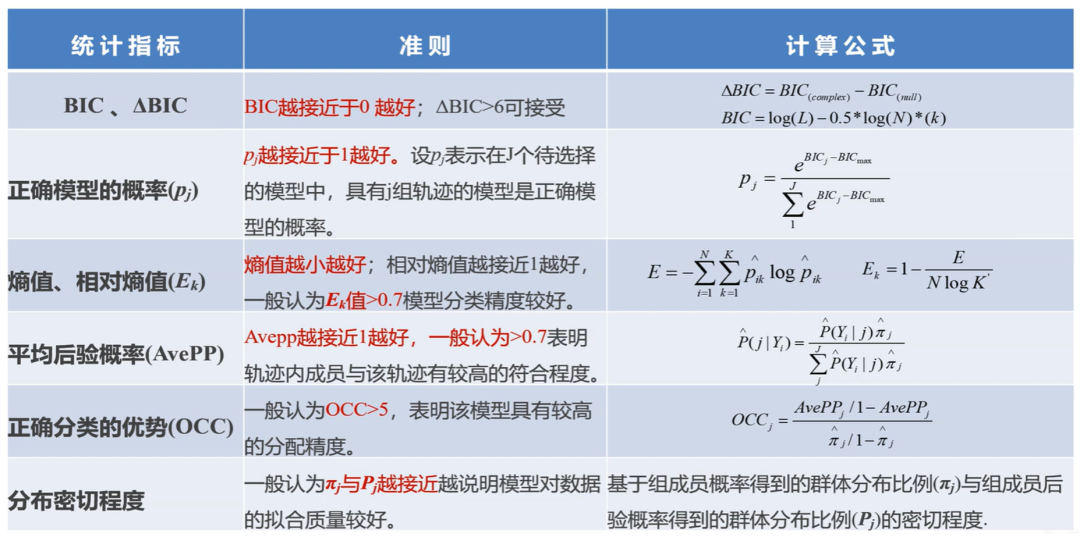
4.群组轨迹模型/组基轨迹模型(GBTM)的模型选择方法

5.群组轨迹模型/组基轨迹模型(GBTM)的进一步分析

本公众号回复“沙龙”即可获得PPT,数据等资料 |
本公众提供各种科研服务了!
一、课程培训 2022年以来,我们召集了一批富有经验的高校专业队伍,着手举行短期统计课程培训班,包括R语言、meta分析、临床预测模型、真实世界临床研究、问卷与量表分析、医学统计与SPSS、临床试验数据分析、重复测量资料分析、nhanes、孟德尔随机化等10余门课。如果您有需求,不妨点击查看: 二、数据分析服务 浙江中医药大学郑老师团队接单各项医学研究数据分析的服务,提供高质量统计分析报告。有兴趣了解一下详情: |







 本文介绍了轨迹增长模型,一种处理纵向数据异质性的方法,区分了潜类别混合增长模型和群组轨迹模型。通过实例展示群组轨迹模型在研究中的应用,探讨了社交和智力活动如何影响认知轨迹,强调了考虑个体差异的重要性。
本文介绍了轨迹增长模型,一种处理纵向数据异质性的方法,区分了潜类别混合增长模型和群组轨迹模型。通过实例展示群组轨迹模型在研究中的应用,探讨了社交和智力活动如何影响认知轨迹,强调了考虑个体差异的重要性。
















 7465
7465

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








