4.1 数学期望
1. 离散型随机变量的数学期望
- E(X):随机变量X取值的加权平均值,权重为概率,级数𝑖=1∞𝑥𝑖𝑝𝑖收敛,则
- 0-1分布X~B(1, p):E(x) = p
- 二项分布X~(n, p):E(X) =np
- 指数分布X~e(𝛌):E(X) =
- 0-1分布X~B(1, p):E(x) = p
- 几何分布X ∼ G(p):E(X) =
- 超几何分布:E(X) =
2. 连续型随机变量的数学期望:
- 均匀分布X ∼ U(a, b):
- Gamma 分布𝐗~𝚪(𝜶, 𝜷):
3. 随机变量函数的数学期望
- 一维随机变量:
- 离散型:X 为离散型随机变量,其分布律为
,k = 1, 2, ..., y = g(x) 是 x 的 (分段) 连续函数或单调函数,且级数
绝对收敛,则对Y = g(X),我们有

-
公式的意义:求E(Y)时,不必算出的分布律或概率密度,而只要利用X的分布律或概率密度就可以了
-
- 连续型:若X为连续型的,其密度函数为f(x),且反常积分
绝对收敛,则有

- 离散型:X 为离散型随机变量,其分布律为
- 二维随机变量:设 (X, Y) 是二维随机变量
-
离散型:若 (X, Y) 是离散型,二维概率分布律为
。g(x, y) 是分片连续函数,且级数
绝对收敛,则有
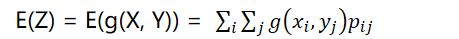
-
连续型:若(X, Y)为连续型,其二维密度函数为f(x, y),且反常积分
绝对收敛,则有


-
4. 数学期望的性质
- E(C) = C
- E(CX) = CE(X)
- E(aX + bY) = aE(X) + bE(Y)
- 若 X 和 Y 独立,E(XY) = E(X) E(Y)
- g(X) 和 h(Y) 也是独立的随机变量,E(g(X)h(Y)) = E(g(X))E(h(Y))
4.2 方差和矩
1. 方差的定义及计算
- 方差:随机变量 X 取值在期望 E(X) 周围的集中程度
-
定义:
- 公式反映
- D(X) ≥ 0
- D(X) ≤ E(
)常用于估计方差上界
-
X为离散型:
- X为连续型:
- 均方差标准差
:反映了随机变量和均值的典型距离
- 公式反映
- 0-1分布X~B(1, p):D(x) = p(1-p)
- 二项分布X~(n, p):D(X) =np(1-p)
- 泊松分布𝐗~𝐏(𝝀):D(X) =𝜆
-
- 几何分布X ∼ G(p):D(X) =
- 几何分布X ∼ G(p):D(X) =
- 均匀分布X ∼ U(a, b):D(X) =
- Gamma 分布𝐗~𝚪(𝜶, 𝜷):D(X) =
- 指数分布𝐗~𝐞(𝝀):D(X) =
2. 方差的性质
- D(C) = 0
- D(aX+b) =
- 若X与Y独立,则

-
随机变量
相互独立,
是n个常数,则
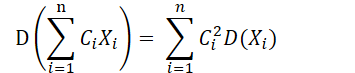
- D(X) = 0 等价于 P(X = E(X)) = 1
- 此时X 服从退化分布
-
3. 变异系数、原点矩及中心距
- 变异系数:在比较两个随机变量的取值集中程度时消除方差和标准差的量纲,衡量了 X 取值在 E(X) 周围的相对集中程度(越小越集中)
- 定义:若随机变量 X 的期望、方差均存在, 且 E(X) ≠ 0, 则

-
随机变量的原点矩和中心距: 是非负整数
-
X 的 k 阶原点矩:
-
X 的 k 阶中心矩:
-
- 中心距可以用原点矩表示:
-
4.3 协方差和相关系数
1. 协方差
- 定义:Cov(X, Y) = E(X − E(X))(Y − E(Y)) = E(XY) − E(X)E(Y)
- 特别情况:Cov(X, X) = D(X)
- 计算
- 离散型

- 连续型
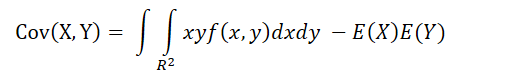
- 离散型
-
协方差的性质
-
Cov(X, Y) = Cov(Y, X)
- Cov(aX, Y) = a Cov(X, Y)
- Cov(X + Y, Z) = Cov(X, Z) + Cov(Y, Z)
- Cov(X, a) = 0
- Cov(X, Y) = E(XY) − E(X)E(Y)
- 若 X, Y 独立, 那么, Cov(X, Y) = 0
- D(X ± Y) = D(X) + D(Y) ± 2 Cov(X, Y)
-
- 均值向量:
-
协方差阵:

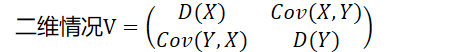
- 多项分布的协方差

- 超几何分布的协方差

- 超几何分布的方差
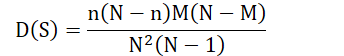
2. 相关系数
- 协方差反映随机变量 X 与 Y 的线性相关关系, 但它受量纲的影响:Cov(aX, bY) = ab Cov(X, Y)。我们将根据协方差定义出一个不受量纲影响的相关系数
- 定义:
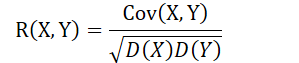
- R(X, Y) = 0 时, X 和 Y不相关
- R(X, Y) > 0 时,X 和 Y正相关
- R(X, Y) < 0 时,X 和 Y负相关
- R(X, Y) = ±1 时, X 和 Y 为完全的线性关系
- R(X, Y) = 1 时,X 和 Y 完全正相关
- R(X, Y) = −1 时,X 和 Y 完全负相关
-
注意:独立性蕴含不相关性, 反之未必
-
性质
- R(X,Y)=R(Y,X)
- |R(X,Y)|≤1
- |R(X, Y)| = 1 的充要条件为:存在常数 a, b, 且 a = 0,使得 P(Y = aX + b) = 1
- (X与Y线性相关)
























 2564
2564

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








