（2）三相异步电动机定子串不对称电抗起动过程仿真分析

一仰众山高

已于 2025-02-12 11:29:06 修改

阅读量1k

点赞数 26

分类专栏：三相异步电动机各种起动方法的建模仿真文章标签： matlab 算法软件工程

于 2024-07-09 18:35:54 首次发布

本文链接：https://blog.csdn.net/weixin_45670943/article/details/140295829

版权

三相异步电动机各种起动方法的建模仿真专栏收录该内容

4 篇文章

订阅专栏

1. 概述

2. 三相感应电动机状态方程式

3. 基于Level2 S-Function的仿真模型建立

4. 动态分析实例

5. 总结

6. 参考文献

1. 概述

三相感应电机自然坐标系下的数学模型是一组周期性变系数微分方程（其电感矩阵是转子位置角的函数，转子位置角随时间按正弦规律变化），将其用于电机控制系统的设计和控制策略的分析定制也许不太合适，有点勉为其难。而将其用于理解电机的基本物理原理和数学特性，设计更高效的电机和优化算法；对分析三相感应电机的启动、运行和制动等状态，深入理解电机的工作原理和学生工程师的教育培训；提供电机的故障诊断和分析的详细信息；用于电机与机械系统的耦合分析等也许是非常合适的。本文根据三相感应电动机定子自然坐标系下的状态方程，用Matlab建立了基于Level2 S-Function的仿真模型，然后应用这个仿真模型对三相感应电动机定子串不对称电抗的起动过程进行了仿真分析，并用对称分量法分析定子电路一相串联电抗器时的不对称系统，确定起动电抗的数值。对仿真结果进行比较分析，得出了一些有用的结论。

2. 三相感应电动机状态方程式

在建立三相感应电动机动态数学模型时，为简单起见作如下假设：（1）气隙磁通密度在空间按正弦分布，忽略磁场的高次谐波；（2）忽略磁路饱和影响及铁心损耗；（3）定、转子绕组均为三相对称绕组，其电阻和漏感为常数。三相感应电动机在相坐标系下的数学方程如下：

2.1电压方程

设在相坐标系下定、转子各绕组电压、电流的正方向符合电动机惯例，电流、磁链的正方向符合右手螺旋定则，对每个绕组电路分别应用KVL，得到矩阵形式的电压方程为：

$[u^{}]=[R^{}][i^{}]+p^{}([L^{}][i^{}])$ （1）

式中，

$\begin{bmatrix}u\end{bmatrix}=\begin{bmatrix}u_A&u_B&u_C&u_a&u_b&u_c\end{bmatrix}^T$ ， $\begin{bmatrix}i\end{bmatrix}=\begin{bmatrix}i_A&i_B&i_C&i_a&i_b&i_c\end{bmatrix}^T$ ‘

$\begin{bmatrix}R\end{bmatrix}=diag\begin{bmatrix}R_{s} & R_{s} & R_{s} & R_{r} & R_{r} & R_{r}\end{bmatrix}$ ，

$\begin{bmatrix}L\end{bmatrix}=\begin{bmatrix}L_s&-M_{ss}&-M_{ss}&M_{sr}\cos\theta_1&M_{sr}\cos\theta_3&M_{sr}\cos\theta_2\\-M_{ss}&L_s&-M_{ss}&M_{sr}\cos\theta_2&M_{sr}\cos\theta_1&M_{sr}\cos\theta_3\\-M_{ss}&-M_{ss}&L_s&M_{sr}\cos\theta_3&M_{sr}\cos\theta_2&M_{sr}\cos\theta_1\\M_{sr}\cos\theta_1&M_{sr}\cos\theta_2&M_{sr}\cos\theta_3&L_r&-M_{rr}&-M_{rr}\\M_{sr}\cos\theta_3&M_{sr}\cos\theta_1&M_{sr}\cos\theta_2&-M_{rr}&L_r&-M_{rr}\\M_{sr}\cos\theta_2&M_{sr}\cos\theta_3&M_{sr}\cos\theta_1&-M_{rr}&-M_{rr}&L_r\end{bmatrix}$ ，

$u_A,u_B,u_C$ ：分别为定子A、B、C三相绕组端电压；

$u_a,u_b,u_c$ ：分别为转子a、b、c三相绕组端电压；

$i_A,i_B,i_C$ ：分别为定子A、B、C三相绕组电流；

$i_a,i_b,i_c$ ：分别为转子a、b、c三相绕组电流；

$\text{p}$ ：微分算子d/dt； $R_s$ : 定子每相绕组电阻； $R_r$ : 折算到定子的转子每相绕组电阻；

$M_{ss}$ : 定子绕组之间互感； $M_{rr}$ : 转子绕组之间互感；

$L_{s}$ : 定子绕组全自感; $L_{r}$ : 折算到定子绕组的转子绕组全自感;

$M_{sr}$ : 定、转子绕组间的互感;

$\theta_1=\theta\text{,}\theta_2=\theta-2\pi/3\text{,}\theta_3=\theta+2\pi/3$ : $\theta$ : 定、转子A a相绕组间的夹角。

2.2 转矩方程

$T_e=\frac{n_p}2([i]^T\frac\partial{\partial\theta}[L][i])$ （2）

式中， $n_{p}$ ：电机的磁极对数。

2.3 运动方程

$T_e-T_L-R_\Omega\Omega=J\frac{d\Omega}{dt}$ （3）

式中，Te—电磁转矩；TL—负载转矩；RΩ—旋转阻力系数；Ω—转子角速度。J—机组转动惯量。

2.4 状态方程

为了方便编写仿真程序，把电流i、角速度Ω、转角θ作为状态变量，将式（1）和式（3）写成状态方程：

$\begin{aligned}&p[i]=-[L]^{-1}([R]+p[L][i])+[L]^{-1}[u]\\&p\Omega=\frac{n_p}{2J}([i]^T\frac\partial{\partial\theta}[L][i])-\frac{R_\Omega}J\Omega-\frac{T_L}J\\&p\theta=n_p\Omega\end{aligned}$ （4）

3. 基于Level2 S-Function的仿真模型建立

根据以上数学模型，用Simulink建立的ABC相坐标系下的三相感应电动机仿真模型如图1~图3所示，其中，图1中的子系统ABC phase IM-SI表示的是三相感应电动机，图2子系统磁链和电磁转矩方程是用Level 2 S-Function 表示的，S函数取名为TPIM_ABC_Level_2。这个仿真模型可以作为通用的仿真模型使用，可以用于三相感应电动机电源电压不对称、定转子绕组回路串电阻或电抗起动、调速以及绕组开路故障等的动态行为的仿真分析。如果要考虑主磁路饱和因素，可以在S函数中加以补充。如果要对三相感应电机的定子绕组故障（一相开路，两相短路等）、定子绕组回路串电阻（电抗）起动以及转子绕组回路串电阻起动等可以在图2子系统1中进行修改来达到仿真的目的。S函数的程序代码如下：

图1. 三相感应电动机ABC相坐标系下的仿真模型（基于Level 2 S-Function）

图2. 图1子系统ABC phase IM-SI的内部情形

图3. 图2子系统磁链和电磁转矩方程的内部情形

function TPIM_ABC_level_2(block)
   setup(block);
function setup(block)

% Register the number of ports
block.NumInputPorts = 1;
block.NumOutputPorts =1;

% Set up the input port properties
block.InputPort(1).Dimensions = [7,1];
block.InputPort(1).DirectFeedthrough = true;
block.InputPort(1).DatatypeID = 0;
block.InputPort(1).Complexity = 'Real';
block.InputPort(1).SamplingMode = 'Sample';

  
% Set up the output port properties
block.OutputPort(1).Dimensions = [7,1];
block.OutputPort(1).DatatypeID = 0; % double
block.OutputPort(1).Complexity = 'Real';
block.OutputPort(1).SamplingMode = 'Sample';

% Register the parameters
block.NumDialogPrms = 6;
block.DialogPrmsTunable = {'Tunable','Tunable','Tunable',...
                           'Tunable','Tunable','Tunable'};

% Set up the continuous states
block.NumContStates = 0;

% Register the continuous states

block.RegBlockMethod('Outputs',@Outputs);
block.RegBlockMethod('SetInputPortSamplingMode', @SetInputPortSamplingMode);

%endfunction

function Outputs(block)
% 获取输入向量 u
u = block.InputPort(1).Data; % 获取输入向量 u

% 获取参数值
Lss = block.DialogPrm(1).Data;
Lrr = block.DialogPrm(2).Data;
 Ms = block.DialogPrm(3).Data;
 Mr = block.DialogPrm(4).Data;
Lsr = block.DialogPrm(5).Data;
 np = block.DialogPrm(6).Data;

u1=block.InputPort(1).Data(1); 
u2=block.InputPort(1).Data(2); 
u3=block.InputPort(1).Data(3); 
u4=block.InputPort(1).Data(4); 
u5=block.InputPort(1).Data(5); 
u6=block.InputPort(1).Data(6); 
u7=block.InputPort(1).Data(7); 

ang=2/3*pi;
Ls=[Lss -Ms -Ms;
   -Ms  Lss -Ms;
   -Ms -Ms  Lss];

Lr=[Lrr -Mr -Mr;
   -Mr  Lrr -Mr;
   -Mr -Mr  Lrr];

Msr=[Lsr*cos(u1),Lsr*cos(u1+ang),Lsr*cos(u1-ang);
     Lsr*cos(u1-ang),Lsr*cos(u1),Lsr*cos(u1+ang);
     Lsr*cos(u1+ang),  Lsr*cos(u1-ang),Lsr*cos(u1)];

Mrs=[Lsr*cos(u1),Lsr*cos(u1-ang),Lsr*cos(u1+ang);
     Lsr*cos(u1+ang), Lsr*cos(u1),Lsr*cos(u1-ang);
     Lsr*cos(u1-ang), Lsr*cos(u1+ang),Lsr*cos(u1)];

L=[Ls Msr; Mrs Lr];

dMsrdtheta=[-Lsr*sin(u1), -Lsr*sin(u1+ang), -Lsr*sin(u1-ang);
            -Lsr*sin(u1-ang),-Lsr*sin(u1),  -Lsr*sin(u1+ang);
            -Lsr*sin(u1+ang),-Lsr*sin(u1-ang),-Lsr*sin(u1)];

dMrsdtheta=[-Lsr*sin(u1), -Lsr*sin(u1-ang),  -Lsr*sin(u1+ang);
            -Lsr*sin(u1+ang), -Lsr*sin(u1), -Lsr*sin(u1-ang);
            -Lsr*sin(u1-ang), -Lsr*sin(u1+ang), -Lsr*sin(u1)];

dLdtheta =[zeros(3,3) dMsrdtheta; dMrsdtheta zeros(3,3)];

Psi=[u(2);u(3);u(4);u(5);u(6);u(7)];
I=L\(Psi);
Te=I'*dLdtheta*I*np;

block.OutputPort(1).Data =[I(1);I(2);I(3);I(4);I(5);I(6);Te];

%endfunction

4. 动态分析实例

在三相笼型感应电动机拖动生产机械中，有些生产机械要求快速起动，这时可以采用直接起动和电容起动；但有些生产机械要求平滑地慢加速起动，此时可采用定子电路一相串联电抗器起动[1]，三相笼型感应电动机定子电路一相串联电抗器时，将造成定子三相电压不对称，电机运行在不平衡状态，由负序电压所产生的转矩分量具有制动性质，使总的合成转矩降低，以减轻对机构的冲击，使之平稳加速。这里对这种起动方法的起动过程进行仿真分析。为了得到三相感应电动机定子串联不对称电抗器时的起动特性，首先用对称分量法分析定子电路一相串联电抗器时的不对称系统，计算起动电抗的数值，然后用上面所建立的三相感应电动机仿真模型进行仿真。

4.1 定子电路一相串联起动电抗的计算

三相感应电动机定子一相串联电抗时将造成定子三相电压不对称。对于不对称系统可采用对称分量法进行分析。感应电动机正、负序等效电路如图4所示。

(a) 正序电路 (b) 负序电路

图4 感应电动机稳态等效电路

电动机起动时，转差率S=1，三相异步电动机的正、负序等效电路在形式上是相同的。忽略激磁电阻，这样从定子端看进去的总阻抗为Z=Z+=Z-=Z1+Z2Zm/(Z2+Zm)。其中，Z1=Rs+jXslσ,Z2=Rr+jXrl,Zm=jXm。设三相定子绕组Y形联接。用对称分量法分析，可得定子电路一相(b相)串联起动电抗Xst时的正序电压和负序电压分别为：

$U_{+}=U_{a} \frac{3Z + jX_{st}}{3Z + 2 jX_{st}}\\U_{-}=-U_{a} \frac{jX_{st}}{3Z + 2 jX_{st}}$ （5）

式中，U+、U-、Ua均为复数电压，其中Ua为a相电源电压。

定子正序电流和负序电流分别为：

$I_{1+}=U_+/Z\\I_{1-}=U_-/Z$ （6）

转子正序电流和负序电流分别为：

$I_{2+}=I_{1+}(Z-Z_{1})/(R_{r}+jX_{rl})\\I_{2-}=I_{1-}(Z-Z_{1})/(R_{r}+jX_{rl})$ （7）

电机的起动转矩为：

$T_{st}=\frac{3n_p}{2\pi f}R_r(\left|I_{2+}\right|^2-\left|I_{2-}\right|^2)$ （8）

式中，np —电机磁极对数； f —电源频率。

根据生产机械的要求，确定Tst的具体数值后，即可求得起动电抗Xst。电动机定子电路一相串联起动电抗降低的起动转矩应大于负载的起动转矩。

4.2 仿真分析

仿真用的笼型三相感应电动机参数：

4极、2.2kw、380V、50Hz，定子绕组为Y接法，参数为Rs=2.68/Ω，Rr=2.85/Ω，Lsl=0.18067/H，Lr=0.18067/H，Mss=Mrr=0.08433/H，Msr=0.16866/H。电动机和负载转矩的总转动惯量J=0.03kg.m2。

根据方程式（5）~（8）用matlab编写仿真程序，对定子电路一相(B相)串联起动电抗Xst 进行计算。

当电源电压为三相对称额定电压，设a相电压的初相角为零时，电机定子电路一相（b相）串联起动电抗Xst=4.77/Ω及Xst=13.38/Ω（分别按串电抗时的起动转矩与直接起动时的起动转矩之比为0.75和0.5计算）带额定负载起动，当转速接近额定速时切除起动电抗器（t=0.23秒和t=0.32秒）时的瞬态特性曲线如图5所示。

为便于比较，对额定负载下直接起动过程也进行了仿真计算，其转速和转矩随时间的变化曲线如图5（a）上图所示，起动转矩的正向最大峰值约为73.8/N.m，起动时间约为0.185秒。A相电流最大峰值约为40.0/A（未给出曲线）。若电机定子电路串联三相对称电抗Xst=1.74/Ω（按串电抗时的起动转矩与直接起动时的起动转矩之比为0.75计算）带额定负载起动，起动时间约为0.28秒（未给出仿真曲线）。

当Xst=4.77 /Ω时，起动转矩的正向最大峰值约为60 / N.m，起动时间约为0.23秒。定子a相电流最大峰值（正向）约为40/A，b相电流最大峰值(反向)约为23.2 / A，c相电流最大峰值(反向)约为40/A.；当Xst=13.38 /Ω时，起动转矩的最大峰值约为60 / N.m，起动时间约为0.23秒。定子A相电流最大峰值（正向）约为40 / A，B相电流最大峰值(反向)约为23.4 / A，C相电流最大峰值（反向）约为40 / A。

从图5可以看出，三相感应电动机定子一相串联电抗起动时，定子三相电流不对称，B相电流最小，起动转矩峰值比直接起动时小，起动时间较长；在起动初期，起动转矩按电源频率脉振，当转速达到一定数值时，转矩按二倍电源频率脉振。

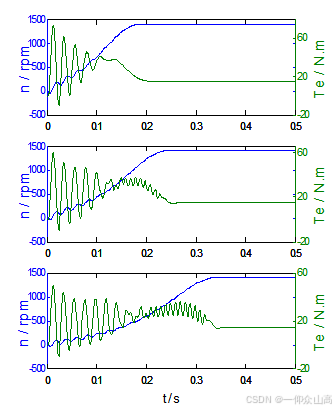
(a) 转速和转矩特性

(b) 定子电流特性（Xst=4.77/Ω）

图5 三相感应电动机定子B相串电抗起动时的动态特性

5. 总结

本文根据三相感应电动机在定子ABC相坐标系下的数学模型，用matlab/simulink建立了基于Level 2 S-Function的仿真模型，应用对称分量法导出了三相感应电动机定子一相串联电抗起动时的起动转矩表达，用Matlab编程对起动电抗值进行计算。起动电抗的数值可按生产机械对起动时冲击转矩和起动时间的具体要求，用式（8）进行初步计算，然后通过计算机仿真的调整来较准确地加以确定。三相感应电动机定子一相串联电抗起动，起动装置简单，可以有效地限制起动转矩，延长起动时间，适合于某些生产机械对起动的要求。