PeFAD: A Parameter-Efficient Federated Framework for Time Series Anomaly Detection

最新推荐文章于 2025-04-27 21:26:32 发布

萧宛亦

最新推荐文章于 2025-04-27 21:26:32 发布

阅读量750

点赞数

文章标签：深度学习人工智能机器学习

原文链接：https://arxiv.org/abs/2406.02318

版权

系列文章目录

PeFAD：用于时间序列异常检测的参数高效联合框架 KDD 24

摘要

随着移动传感技术的普及，各个领域产生和积累了大量的时间序列数据，推动了大量的实际应用。在这种情况下，时间序列异常检测实际上很重要。它致力于从时间序列中的正态样本分布中识别出异常样本。现有方法通常假设所有时间序列都在中心位置可用。然而，由于各种边缘设备的部署，我们正在见证时间序列的去中心化收集。为了弥合去中心化时间序列数据和集中式异常检测算法之间的差距，随着隐私问题的日益增加，我们提出了一种名为 PeFAD 的参数高效联合异常检测框架。 PeFAD首次采用预训练语言模型（PLM）作为客户本地模型的主体，可以受益于其跨模态知识转移能力。为了减少通信开销和本地模型适应成本，我们提出了一种参数高效的联邦训练模块，这样客户端只需要微调小规模参数并将其传输到服务器进行更新。 PeFAD 利用一种新颖的异常驱动掩模选择策略来减轻训练期间被忽视的异常的影响。还提出了对所有客户端共享的合成隐私保护数据集进行知识蒸馏操作，以解决客户端之间的数据异构性问题。我们对四个真实数据集进行了广泛的评估，其中 PeFAD 的性能比现有最先进的基线高出 28.74%。

一、引言

示例：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。
图 1：分散时间序列异常检测的图示。 “红色圆圈”表示异常点或异常模式。每个场景中，机构之间不允许数据共享，而是通过服务器协调来促进协同训练。

随着各种传感器和移动设备的增加，大量的时间序列数据以分散的方式被收集，从而实现了各种时间序列应用[18,19,31,34]，例如故障诊断[7]和欺诈检测[ 2]。这些应用程序的一个基本方面是时间序列异常检测 [38]，如图 1 所示，其目的是发现时间序列中可能指示错误或其他需要进一步调查的异常情况的异常观察或趋势。

由于其重要性，大量研究致力于发明有效的时间序列异常检测模型 [2, 38]，包括基于传统统计 [11, 29] 和神经网络 [38] 的方法。由于注释异常的困难，无监督方法成为主流方法，主要可分为基于重建的方法[38, 45]和基于预测的方法[33, 42]。前者根据重建误差识别异常，而后者根据预测误差识别异常。在现实场景中，时间序列数据通常由分布在不同位置的边缘设备（例如传感器）生成。然而，大多数现有的时间序列异常检测模型通常需要集中的训练数据，这使得它们在分散的场景中效果较差。由于人们对隐私保护的日益关注，数据提供者可能不愿意披露他们的数据。例如，信贷机构 Equifax 经历了一次数据泄露事件 [46]，暴露了社会安全号码和其他敏感数据，严重影响了个人的财务安全。因此，去中心化时间序列异常检测已成为实现隐私保护[16]和确保数据访问限制[17]的关键问题。

最近，联邦学习（FL）提供了一种使用分布在多个客户端上的分散数据来训练模型的解决方案 [16, 39]。 FL 是一种机器学习设置，许多客户端在中央服务器的编排下协作训练模型，同时保持数据分散。在本研究中，我们的目标是开发一种用于无监督时间序列异常检测的新型 FL 框架，以弥合去中心化数据处理和无监督时间序列异常检测之间的差距。

然而，由于以下三个挑战，开发基于联邦学习的时间序列异常检测模型并非易事。首先，联邦学习背景下处理数据稀缺问题具有挑战性。由于数据收集机制的限制（例如低采样率）和数据隐私问题，客户端本地数据可能非常稀疏，尤其是少数异常数据。在分散训练数据的情况下，依赖于足够训练数据的现有方法的性能可能会显着下降。其次，现有的无监督方法 [38, 45] 经常忽视训练期间异常的存在。这可能会严重扰乱基于预测和重建的方法的训练过程，影响它们准确识别异常的能力[37]。例如，在基于重建的方法中，如果屏蔽的时间序列片段没有覆盖训练中的异常时间点，则学习的时间序列重建模型对异常的敏感度将降低[35]。第三，由于本地数据的异构性，也很难获得一个能够很好地推广到所有客户的全局模型。跨不同边缘设备收集的时间序列通常是异构的和不相同的分布[41]。由于不同局部时间序列数据集之间的分布漂移，FL 模型通过简单聚合局部模型来实现最优全局模型并非易事。

为了解决上述挑战，本文提出了一种名为 PeFAD 的参数高效联合时间序列 AnomalyDetection 框架。 PeFAD采用水平联邦学习模式，许多客户端在中央服务器的编排下使用本地训练数据协作训练全局模型。 PeFAD包含两个主要模块：基于PLM的本地训练模块和参数高效的联合训练模块。基于 PLM 的本地训练模块为每个客户端采用预先训练的语言模型 (PLM)，该模型具有异常驱动的掩模选择策略和保护隐私的共享数据集合成机制。我们采用PLM作为客户本地模型的主体，因为它的跨模态知识传递能力[9,14,45]可以有效解决数据稀缺的挑战。具体来说，我们的目标是利用 PLM 的通用知识和上下文理解能力来帮助识别时间序列模式和异常。为了减少 PLM 的计算和通信开销，我们提出了一种参数高效的联合训练模块。客户端只需要微调小范围的参数，然后将它们传输到服务器。为了减轻训练期间异常的影响，我们提出了一种新颖的异常驱动掩模选择策略，首先在训练期间识别异常，然后为它们分配更大的权重以选择进行掩模。为了减轻客户端之间的数据异构性，我们提出了一种保护隐私的共享数据集合成机制。具体来说，每个客户端首先利用变分自动编码器来合成隐私保护时间序列，并将合成的数据汇集在一起形成所有客户端共享的数据集。然后使用共享数据集在本地模型和全局模型之间进行知识蒸馏，以实现客户端之间更一致的模型更新。

我们的主要贡献总结如下。

• 据我们所知，这是第一个基于PLM 的无监督时间序列异常检测联合框架。为了减少计算和通信成本，我们提出了一种参数高效的联合训练模块。
• 为了减轻训练过程中异常的影响，提出了异常驱动的掩模选择策略，增强了模型对变化点的适应性，从而提高了异常检测的鲁棒性。
• 为了处理客户端之间的数据异构性，提出了一种新颖的隐私保护共享数据集合成机制和知识蒸馏方法，以确保客户端之间的模型更新更加一致。
• 我们对四个流行的时间序列数据集进行了广泛的评估。结果表明，所提出的 PeFAD 在集中式和联合式设置中均显着优于现有的 SOTA 基线。

本文的其余部分组织如下。第二节回顾相关工作并分析现有工作的局限性。第 3 节介绍了初步概念和联合时间序列异常检测问题。然后，我们在第 4 节中提出我们的解决方案，然后在第 5 节中进行实验评估。第 6 节讨论了本文的结果和动机，第 7 节对本文进行了总结。

2 RELATEDWORK

2.1 Time Series Anomaly Detection

时间序列异常检测旨在识别时间序列中的异常模式或异常值，这在各种实际应用中发挥着至关重要的作用[26, 38]。传统上，时间序列异常检测方法大多基于传统的机器学习模型，例如支持向量机（SVM）[26]和隔离森林[11]。上述方法的主要局限性在于，由于学习能力有限，难以捕获时间序列的复杂时间相关性。近年来，随着深度学习技术的进步，深度神经网络模型已广泛用于时间序列异常检测，可分为有监督方法和无监督方法。监督方法 [21] 在标记数据上进行训练，以识别时间序列中正常模式的偏差。无监督方法 [38, 45] 通常计算异常分数来衡量原始时间序列与重建或预测时间序列之间的差异。无监督方法可以学习标签之外的时间序列的内在结构和模式。然而，现有的时间序列异常检测方法大多使用集中式数据进行训练，并且计算量很大，限制了它们在资源受限的边缘设备上的使用。

2.2 Federated Learning

联合学习 (FL) 是一种机器学习方法，其中许多客户端（通常称为边缘设备）使用分散数据协作训练模型 [5,12,13,16,24]。通常，根据客户端之间数据特征和样本空间的重叠，FL可以分为水平联邦学习、垂直联邦学习和联邦迁移学习[16]。水平FL[5]被定义为不同客户端上的数据集共享相同特征空间但具有不同样本空间的情况，而垂直FL[12]是相反的情况。在联邦迁移学习[24]中，跨客户端数据之间的样本空间和特征空间实际上是不重叠的。在本研究中，我们考虑基于水平 FL 的时间序列异常检测。

最近，出于隐私保护的考虑，FL已被应用于时间序列，例如时间序列预测[17]和异常检测[10]。然而，现有的研究缺乏对如何在联邦环境中使用预训练的语言模型进行时间序列异常检测的深入探索，在现有文献中留下了很大的空白。这种差距可归因于应用预训练语言模型时在联邦学习背景下协调域差异和任务变化相关的固有复杂性。

3 PROBLEM DEFINITION

我们首先提出必要的预备知识，然后定义要解决的问题。为了使符号一致，我们使用粗体字母来表示矩阵和向量。

定义 3.1（时间序列）。时间序列 $T=\langle t_{1},t_{2},\cdots,t_{m}\rangle$ 是𝑚 观测值的时间排序序列，其中每个观测值 $t_i\in\mathbb{R}^D$ 是一个 𝐷 维向量。如果 𝐷 = 1，则 𝑇 是单变量，如果 𝐷 > 1，则𝑇 是多变量。

联合时间序列异常检测。给定一个服务器 S 和 N 个客户端（例如传感器）及其本地时间序列数据集 $\mathcal{D} = \{\mathcal{T}_{1},\mathcal{T}_{2},\cdots,\mathcal{T}_{\mathcal{N}}\}$ ，每个数据集 $\mathcal{T}_{i}$ 是一组时间序列，即 $\mathcal{T}_{i}=\left\{T_{1}^{i},T_{2}^{i},\cdots,T_{n}^{i}\right\}$ 。我们的目标是学习一个共享的全局函数 $\mathcal{F}(\theta)$ ，它可以检测不同客户端的时间序列中的异常情况。最优全局模型参数 $\theta_{g}^*$ 计算如下：
在这里插入图片描述
其中 $\mathcal{L}(\theta_{g};\mathcal{T}_{i})$ 表示客户端 𝑖 的损失函数， $\theta_{g}$ 表示全局模型的参数。 C 表示客户端集合。

在客户端 𝑖 中，给定时间序列 $T^{i} = \langle t_{1}^{i},t_{2}^{i},\cdots,t_{m}^{i}\rangle$ ，我们的目标是计算每个时间点 𝑗 的异常值分数 $OS(t_j^i)$ 。 $OS(t_j^i)$ 越高意味着 $t_j^i$ 越有可能是异常值。离群值得分可以表述如下：
在这里插入图片描述
其中 $\hat{t}_j^i$ 是 $t_j^i$ 的重建值。我们将 $OS(t_j^i)$ 的顶部 𝑟% 视为异常，其中 𝑟 是阈值。

4 METHODOLOGY

图 2 显示了拟议 PeFAD 的框架概述。如图所示，PeFAD由两大模块组成：基于PLM的本地训练（图右部分）和参数高效的联邦训练（图左部分）。具体来说，在基于PLM的本地训练模块中，客户端首先使用修补机制和异常驱动掩模选择策略（ADMS）对本地时间序列进行预处理，使得模型能够更好地理解时间序列的复杂模式。然后将预处理后的数据输入到基于PLM的本地模型中进行训练。具体来说，预处理后的数据经过嵌入层、堆叠PLM块和输出投影层，最终输出重建的时间序列。客户端根据重构数据，通过计算重构误差来识别异常点。此外，利用保护隐私的共享数据集合成机制（PPDS，图右下部分）通过知识蒸馏来减轻客户端之间的数据异构性。为了减少计算和通信成本，我们还提出了一种参数高效的联合训练模块。接下来我们将分别提供各个模块的技术细节。

4.1 PLM-based Local Training

为了更好地捕获本地时间信息，客户端将本地时间序列划分为不重叠的补丁[20]。具体来说，我们聚合相邻的时间步骤来创建基于补丁的时间序列。这种修补应用允许大幅扩展输入历史时间范围，同时保持令牌长度一致并最大限度地减少变压器模型的信息冗余。然后，我们使用异常驱动的掩模选择策略选择这些补丁的一定比例进行掩模。

4.1.1 Anomaly-Driven Mask Selection.

现有的基于重建的方法[32,38,45]通常忽略训练数据中的异常，这可能会破坏掩模重建。例如，如果正常点被屏蔽，而异常点被用作观测值来重建被屏蔽的时间序列片段，则可能会导致较大的重建误差[37]。为了解决这个问题，我们提出了异常驱动的掩模选择策略，首先识别异常，然后为它们分配更大的权重以选择进行掩模。该模块结合了对补丁内和补丁间变异性的分析来计算补丁的异常分数，捕获补丁特定的偏差和模式随时间的上下文演变。

在这里插入图片描述
图 2：PeFAD 框架概述。 PeFAD 由基于 PLM 的本地训练和参数高效的联合训练组成。

补丁内分解。为了捕获第𝑖补丁（表示为 $P_{i}$ ）的内在特征，我们利用时间序列分解技术[6]。具体来说，我们将每个补丁分解为 𝑀 组件，如式（1）所示。 (3)、提取残差分量计算斑块的异常内得分。

在这里插入图片描述
其中 $g_{j}$ 表示第 𝑗 个分量， $a_{j}$ 是第 𝑗 个分量的系数，𝜀 表示噪声项。

具体来说，我们使用奇异谱分析（SSA）[6]来分解补丁。在SSA中，patch $P_{i}$ 首先通过嵌入转化为Hankel矩阵 $\mathcal{P}_{i}$ ，然后对该矩阵应用奇异值分解（SVD），将 $\mathcal{P}_{i}$ 分解为三个矩阵的乘积： $\mathcal{P}_{i}=U\Sigma V^{T}$ ，其中𝑼和𝑽表示左矩阵和右奇异向量矩阵，𝚺表示奇异值的对角矩阵。然后，原始补丁被重建为

在这里插入图片描述
其中 𝐾 表示 $\mathcal{P}_{i}$ 的非零特征值的数量。 $\sigma_{k}$ 是第 𝑘 个奇异值， $u_{k}$ 是第 𝑘 左奇异向量， $v_{k}$ 是第 𝑘 右奇异向量。

矩阵P𝑖构成了原始补丁的主要结构。例如，趋势、季节性和残差分量对应于矩阵 $\mathcal{P}_{i}$ 的低、中和高频分量。我们可以通过过滤得到这些成分。残差通常包含时间序列中的异常现象[25]。因此，我们提取分解后的残差分量，并计算残差分量的均值作为残差值 $\mathcal{R}_{i}$ ，如式（1）所示。（5）。残差值越高表示出现异常的可能性越大。然后，我们对 $\mathcal{R}_{i}$ 进行归一化，以计算第 𝑖 个补丁的异常分数 $\mathcal{R}_i^{\prime}$ 。
在这里插入图片描述

其中下标𝑘表示矩阵的第𝑘值， $K_{N}$ 表示与通过过滤获得的残差分量相关的奇异值集合。

补丁间相似性评估。补丁间相似性评估提供了对模式补丁动态演化的见解。假设 $\mathcal{A}_{i}$ 是 patch 𝑖 的向量，我们计算第 𝑖 和第 (𝑖-1) 个 patch 之间的余弦相似度。
在这里插入图片描述
余弦相似度的范围是-1到1，值越大表示补丁之间的相似度越高。与之前的补丁相似度较低的补丁更有可能是异常的，因此我们改变单调性并对 $C_{i}$ 进行归一化以计算第𝑖补丁的异常分数 $C_{i}^{\prime}$ 。

补丁的异常分数。我们综合补丁内时间序列分解和补丁间相似性评估，以获得补丁𝑖的最终异常分数，如下所示：
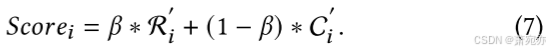
在这里插入图片描述
异常分数超过预定义阈值的补丁被视为异常，并被分配更大的权重以供选择进行屏蔽。由于模型更强调被屏蔽的补丁，异常驱动的屏蔽选择策略可以增强模型对变化点的适应性，从而提高异常检测的鲁棒性。

4.1.2 保护隐私的共享数据集合成。

在联邦学习中，客户端可能具有不同的数据分布和特征，从而带来数据异构性挑战，使得聚合模型的泛化变得困难。为了解决这个问题，我们提出了一种结合知识蒸馏的隐私保护共享数据集合成方案。

保护隐私的共享数据集合成。最近的工作表明，减少互信息可以促进数据集生成中的隐私保护[40]。受这个想法的启发，我们采用约束互信息方法来获取合成数据以保护本地数据的隐私。具体来说，客户端𝑖训练变分自动编码器（VAE）模型以从本地时间序列 $\mathcal{T}_{i}$ 合成时间序列 $\mathcal{T}_{i}$ 。互信息 $I(\mathcal{T}_i;\mathcal{T}_{s,i})$ 衡量 $\mathcal{T}_{s,i}$ 揭示 $\mathcal{T}_{i}$ 的程度。通过约束 $I(\mathcal{T}_i;\mathcal{T}_{s,i})$ ，降低了从 $\mathcal{T}_{s,i}$ 推断出 $\mathcal{T}_{i}$ 的可能性，从而更好地保护数据隐私，并有利于隐私保护时间序列的合成。

在这里插入图片描述

其中𝑝 (𝑥, 𝑦) 表示联合概率分布，𝑝 (𝑥) 和𝑝 (𝑦) 分别作为𝑥 和𝑦 的边际概率。

为了确保合成时间序列的有效性，我们引入了一个约束来保持合成时间序列与原始时间序列之间的分布相似性。我们使用 Wasserstein 距离来量化这种分布相似性 [23]。 Wasserstein 距离越小，表示从一种分布转换到另一种分布的成本越低，这意味着这两个分布更相似。给定两个时间序列 $X=\langle x_{1},x_{2},\ldots,x_{m}\rangle$ 和 $Y=\langle y_{1},y_{2},\ldots,y_{n}\rangle$ ，以及它们的累积分布函数 $F_{X}$ 和 $F_{Y}$ ，可以得到 Wasserstein 距离，如下：

在这里插入图片描述

其中 𝛾 表示 $F_{X}\mathrm{~and~}F_{Y}$ 之间的联合分布，而 $\Gamma(F_X,F_Y)$ 表示具有边际分布 $F_{X}\mathrm{~and~}F_{Y}$ 的所有联合分布的集合。

我们使用VAE来合成时间序列，它由编码器和解码器组成。编码器首先将输入时间序列编码为特征表示，然后解码器尝试基于该表示生成合成时间序列。分别通过约束互信息和 Wasserstein 距离来保证原始数据的隐私性和合成数据的有效性。 VAE 的损失函数由下式给出

在这里插入图片描述
其中 L𝑣𝑎𝑒 表示 VAE 的基本损失函数。 𝒙 和 𝒛 分别表示输入向量和潜在向量。 𝑞(𝒛|𝒙) 和 𝑝 (𝒙|𝒛) 分别表示编码器和解码器的输出分布。 𝐾𝐿(·) 表示 Kullback-Leibler 散度 [30]，其计算公式如下：
在这里插入图片描述
其中 𝑞(𝒛|𝒙) 和 𝑝 (𝒛) 都假设遵循多元高斯分布。 $\mu_{i}\mathrm{~and~}\sigma_{i}$ 是高斯分布的平均值和标准差。

然后，服务器整合来自客户端的合成时间序列以形成共享数据集 $\mathcal{D}_{sh}$ 。请注意，时间序列合成是本地训练之前的一次性离线过程。

在这里插入图片描述
知识蒸馏。我们使用共享数据集进一步执行从全局模型到客户端模型的知识蒸馏，以减少客户端之间的数据异构性。具体来说，我们首先分别获得共享数据集上局部模型和全局模型的学习表示，然后计算两个表示之间的差异。我们使用一致性损失来衡量这种差异。通过减少这种差异，模型可以实现更加一致的客户端更新，从而提高聚合全局模型的性能和稳定性。一致性损失作为局部损失函数的正则化项引入如下，
在这里插入图片描述

其中 $\hat{T}_j^i\mathrm{~and~}T_j^i$ 分别表示客户端 𝑖 第 𝑗 时间序列的重构值和真实值。 $\theta_{i}\mathrm{~and~}\theta_{g}$ 分别表示第 𝑖 局部模型和全局模型的参数。 𝜆 是权衡两个损失项的参数。

4.2 Parameter-Efficient Federated Training

作为一个水平的FL框架，PeFAD由一个中央服务器和多个客户端组成。每个客户端的本地模型由输入嵌入层、堆叠的预训练语言模型 (PLM) 块和输出投影层组成，如图 2 右侧部分所示。使用 GPT2 作为 PLM [22] 。我们首先采用几个线性层将原始时间序列数据嵌入到 PLM 所需的特征表示中。 PLM的输出经过全连接层将GPT2的输出维度转换为数据重建模型需要的维度[45]。

我们将模型参数分为可训练参数 𝜃𝑒 和冻结参数 𝜃𝑝 ，即 𝜃 = (𝜃𝑒, 𝜃𝑝 )。我们冻结了 PLM 中的大部分参数，即 |𝜃𝑒 | ≪|𝜃|。具体来说，冻结参数包括层归一化块和第一个𝑛层（𝑛≥5）。我们选择在微调期间冻结 PLM 的大部分参数，因为它们封装了从预训练阶段学到的大部分通用知识。为了以最小的努力增强下游时间序列异常检测任务，我们对输入输出层以及 PLM 最后一层或三层的某些部分进行了微调，包括注意力层、前馈层和位置嵌入，如下所示它们包含特定于任务的信息，并调整它们使模型能够适应目标领域或任务的细微差别。算法1给出了参数高效联邦训练模块的过程。

服务器端培训。服务器首先将可训练参数 $\theta_{e}$ 发送到客户端进行初始化（第5行）。然后，客户端𝑖通过本地训练更新 $\theta_{e,i}$ （第6行）。最后，服务器接收来自所有客户端的参数并将它们聚合以获得更新的参数 $\theta_{e,g}$ （第7-8行）。

客户端本地培训。客户端从服务器收到 $\theta_{e,g}$ 后，用可训练参数 $\theta_{e,i}$ 和冻结参数 𝜃𝑝 组装整个 PLM 模型（第 10 行）。第 𝑖 个局部模型通过梯度下降更新其参数 $\theta_{e,i}$ （第 11-14 行）。本地训练完成后，客户端将 $\theta_{e,i}$ 发送到服务器进行聚合（第15行）。

重复上述训练过程，直到 PeFAD 根据式（1）收敛。 (1).

在这里插入图片描述

4.3 Overall Objective

在本节中，我们给出了所提出方法的总体目标。对于客户端𝑖，它通过优化损失函数L来更新本地可训练模型参数，并将可训练参数发送到服务器。
在这里插入图片描述
其中 $\hat{T}_j^i\mathrm{~and~}T_j^i$ 分别表示客户端 𝑖 第 𝑗 时间序列的重构值和真实值。 $\theta_i\mathrm{~and~}\theta_g$ 分别表示第𝑖局部模型和全局模型的参数，由可训练参数 $\theta_{e}$ 和冻结参数 $\theta_{p}$ 组成。

服务器在全局迭代轮次中聚合跨客户端的可训练参数以获得全局模型。

在这里插入图片描述
每个客户端的时间序列异常检测是通过利用聚合的全局模型来实现的。为了检测异常，我们将测试时间序列输入到局部模型中以获得其在所有时间点的重建值。时间点 𝑘 的异常分数根据重建误差 𝑟𝑒 计算如下，

在这里插入图片描述
其中 $t_k\mathrm{~and~}\hat{t}_k$ 分别是时间点𝑘的真实值和重建值。

5 EXPERIMENTS

5.1 Datasets and Experiment Setup

5.1.1 数据集。我们在四个现实世界时间序列异常检测数据集上进行了实验：SMD、PSM、SWaT 和 MSL。这4个数据集被现有研究广泛使用，并且是从各个现实世界领域收集的，涵盖互联网数据、服务器运行数据、关键基础设施系统数据和航天器监测系统事件。

• SMD。服务器机器数据集（SMD）[28]是从一家大型互联网公司收集的为期 5 周的数据集，具有 38 个特征维度。
• PSM。池化服务器指标 (PSM) 数据集 [1] 是从 eBay 的多个应用程序服务器收集的，具有 25 个特征维度。
• SWaT。安全水处理（SWaT）数据集[15]是从连续运行的关键基础设施系统的51个传感器获得的。
• MSL。火星科学实验室漫游器（MSL）数据集[8]包含来自航天器监测系统事件意外异常报告的遥测异常数据，具有 55 个特征维度。

5.1.2 基线。我们将 PeFAD 与以下 12 种基线进行比较，包括经典方法：OCSVM [29]、隔离森林 (IF) [11] LOF [3]、GANF [4]、MTGFLOW [43]、基于集中重建的方法：Anomaly Transformer (AT) [ 38]、TimesNet [32] 和 FPT [45]，基于集中预测的方法：Autoformer [33]、Informer [42] 和 FEDformer [44]。此外，我们将 FedAvg [16] 的集中式方法转换为联合版本： AT𝑓𝑙 、 Autoformer𝑓𝑙 、 Informer [42] 和 FEDformer [44] 、 TimesNet𝑓𝑙 和 FPT𝑓𝑙 。我们还将 PeFAD 与 FedTADBench [10] 中性能最佳的模型（即 DeepSVDD）进行比较。

5.1.3 评估指标。采用精度（P）、召回率（R）、F1-Score（F1）和AUC-ROC（AUC，接受者操作特征曲线下的面积）作为评价指标。指标值越高意味着性能越好。

5.1.4 实施细节。我们使用 PyTorch 框架在 NVIDIA RTX 3090 GPU 上实现我们的模型。预训练的语言模型（即 GPT2、BERT、ALBERT、RoBERTa、DeBERTa、DistillBERT 和 Electra）是从 Huggingface 下载的。我们首先通过滑动窗口将时间序列分割成连续的不重叠的片段[27]。补丁长度和批量大小分别设置为 10 和 32。采用 Adam 进行优化。我们采用广泛使用的点调整策略[27,28,36]。我们采用 GPT2 作为 PLM，其中 GPT2 的前八层用于训练。对于 SMD、PSM、SWaT 和 MSL，𝜆 分别设置为 1𝑒1、2𝑒0、2𝑒3 和 15𝑒4。 SMD、MSL、PSM 和 SWaT 的阈值 𝑟 分别设置为 0.5、2、1 和 1。

在这里插入图片描述
表 1：不同方法在四个数据集上的定量结果。 P、R、AUC 和 F1 分别表示精度、召回率、AUC-ROC 和 F1-Score（%）。 “中央。” 代表集中化。

5.2 The Main Result

表1显示了在四个数据集上联邦和集中设置下不同方法的性能比较。在联合设置中，最佳性能用粗体标记，次佳结果用下划线标记。在集中设置中，最佳性能标记为红色。我们用 PeFAD𝑐 来代表 PeFAD 的中心化版本。从表 1 可以看出，与所有四个数据集上的所有联合基线相比，PeFAD 在 F1-Score 和 AUC 方面实现了最佳性能，甚至超过了 SMD 和 PSM 数据集上的所有集中式基线。更具体地说，在 F1-Score 和 AUC 指标方面，PeFAD 平均优于联合基线 3.83%–28.74% 和 3.42%–19.82%。此外，我们可以观察到 PeFAD𝑐 在集中式设置下显示出最佳的整体性能。 FPT 在集中式基线中表现出次优的集成性能，该基线也利用了 PLM。它证明了 PLM 在时间序列异常检测任务中的有效性。然而，FPT 在联合设置下的性能表现出下降。例如，在 SMD 上的 F1-Score 和 AUC 指标上，PeFAD 的表现分别优于 FPT𝑓𝑙 9.85% 和 7.37%。这可能是由于FPT没有采用适合联邦训练的参数高效调整方法，冗余参数可能会影响模型性能。

当将基线模型从集中式设置转移到联邦设置时，观察到性能下降的趋势，这表明时间序列异常检测在联邦环境中变得更加困难。这可能是由于数据共享限制，限制了客户使用较少的数据进行模型训练。然而，PeFAD 在联邦和集中式设置中都表现出了最佳的整体性能，表明其对环境变化的强大适应性。还可以观察到，在某些情况下（即SMD数据集），PeFAD的性能超过了PeFAD𝑐。这可能归因于时间序列数据的多样性。通过联邦学习，在每个本地设备上训练的模型可以更好地捕获其本地数据的多样性。客户端可以根据本地数据的特点获得更具适应性的阈值，而集中设置下获得的单一阈值可能无法容纳整个数据。

在这里插入图片描述

5.3 Ablation Study

为了深入了解 PeFAD 关键方面的影响，我们将 PeFAD 与其四种变体的性能进行了比较，如下所示。 𝑤/𝑜_𝑝𝑝𝑑𝑠：没有隐私保护共享数据集合成（PPDS）机制的 PeFAD； 𝑤/𝑜_𝑎𝑑𝑚𝑠：没有异常驱动掩模选择（ADMS）策略的 PeFAD，其中 ADMS 被随机掩模取代； 𝑤/𝑜_𝑝𝑙𝑚：没有预训练语言模型（PLM）的 PeFAD，被 Transformer 取代。我们分别在数据量最大和最小的SMD和MSL上进行实验。结果如图 3 所示。在这两个数据集上，PeFAD 始终优于没有 PPDS、ADMS 和 PLM 的同类产品。它表明这三个组件对于时间序列异常检测都很有用，因为删除其中任何一个组件都会显着降低性能。

在这里插入图片描述

5.4 Effect of Tuning Strategies and PLMs

5.4.1 各种调优策略的效果。为了测试不同 PLM 调整策略的效果，我们将 PeFAD 与微调不同数量的 PLM 层的策略进行比较，包括不微调 (w/o_ft)、调整最后一层到七层 PLM (PeFAD_t1l - PeFAD_t7l ），并完全微调（PeFAD_fft）。结果如表2所示。我们使用基于GPT2的FPT𝑓𝑙作为参考。人们可以观察到，冻结第一层同时微调最后几层是一种合理的调整策略。通过冻结第一层，模型保留了理解广义知识的能力，而微调最后几层有利于模型适应下游任务，从而实现特定领域知识从预训练模型到时间序列的迁移异常检测任务。具体来说，对于具有更多训练数据的SMD数据集，PeFAD在不同的调整层中保持相对稳定，并在调整最后3层和4层时实现最佳性能。对于较小的MSL数据集，模型性能随着调整层数的增加而下降，在调整最后一层时达到最佳性能。由于篇幅限制，在其他数据集上的实验在附录中提供。在 PeFAD 中，我们选择微调 MSL 的最后一层，并微调其他数据集的最后三层。

结果表明，无论调整层数如何，我们的方法始终优于 FPT。与FPT相比，PeFAD在SMD和MSL上的F1-Score方面分别实现了9.85%和7.09%的性能提升。 PeFAD 将通信成本降低了 41.2% 和 94.9%，这表明了 PeFAD 的效率以及所提出的参数高效联合训练模块的有效性。此外，没有微调（w/o_ft）的 PeFAD 在两个数据集上都优于所有联合基线，这证明了 PLM 卓越的跨模态知识转移能力。 PeFAD_fft 在两个数据集上都没有达到最佳性能，而调整较少，尤其是最后几层，效果更好。这是因为 PLM 的初始层包含通用知识，最后一层更适合学习特定于任务的信息。然而，由于异常数据的稀缺，完全微调可能会增加过度拟合的风险，导致性能下降。

在这里插入图片描述

5.4.2 各种PLM 的影响。接下来，我们研究使用不同 PLM 对模型性能的影响。我们比较了七种主流的预训练模型，即 BERT、ALBERT、RoBERTa、DeBERTa、DistilBERT 和 Electra。结果如图 4 所示。可以看到，GPT2 实现了最佳性能，其次是 DeBERTa。与其他 PLM 相比，GPT2 在 SMD 上的 F1-Score 和 AUC 指标上的性能分别提高了 6.22% 和 5.06%。在 MSL 数据集上，F1-Score 和 AUC 值分别提高了 8.84% 和 6.99%。这是因为 GPT2 在预训练期间接触到了更广泛的环境，使其能够更有效地从时间序列中学习。

5.5 Parameter Sensitivity Analysis

5.5.1 各种掩模比𝑟𝑚和贴片长度𝑙𝑝的影响。接下来我们研究模型对掩模比𝑟𝑚和补丁长度𝑙𝑝的敏感性，由于篇幅限制，我们仅给出SMD上的F1-Score结果作为示例，如图5（a）所示。可以观察到，屏蔽或修补机制的结合可以提高模型性能，证明了这两种机制的有效性。随着𝑟𝑚和𝑙𝑝的增加，模型性能先提高然后下降。当 𝑟𝑚 为 20%、𝑙𝑝 为 10 时，模型性能达到最佳。

5.5.2 合成系列长度的影响。接下来我们研究合成数据长度对模型性能的影响，结果如图 5(b) 所示。具体来说，我们改变 SMD 数据集上每个客户端的合成时间序列的长度。我们观察到 F1-Score 曲线先上升，然后略有下降。一般来说，结果表明，当合成时间序列的长度设置为100时，模型获得最佳性能。随着长度从20增加到100，合成时间序列可以带来更多有用的信息，这有利于模型更有效的表征学习。但长度值太大会导致性能下降。这是因为较长的合成时间序列可能会带来冗余或噪声信息，从而降低模型性能。
在这里插入图片描述

5.6 Case Study

为了直观地展示所提出的 PeFAD 的有效性，我们提供了 SMD 的案例研究，如图 6 所示。图 6（a）显示了通过核密度估计估计的真实时间序列和合成时间序列的分布。图中蓝色曲线表示真实时间序列，橙色曲线表示仅通过互信息（MI）约束获得的合成时间序列，红色曲线表示仅通过Wasserstein距离（WD）约束获得的合成时间序列，绿色曲线表示在 MI 和 WD 联合约束下合成的时间序列。可以看到橙色曲线与蓝色曲线表现出显着差异，而红色曲线与真实分布（蓝色曲线）非常相似。这是因为仅仅减少互信息忽略了对合成数据质量的考虑。然而，绿色曲线既保证了分布相似性，又通过互信息保护了数据的隐私。

图 6(b) 显示了客户端测试期间 SMD 数据集的时间序列重建和异常检测的示例。人们可以观察到，正常点的估计值非常接近真实值，而在异常点，估计值更接近于不受异常影响的合理值。因此，通过评估估计值和实际值之间的差异，可以成功识别时间序列中的异常情况。这可能归功于提出的 ADMS 策略和 PPDS 机制，它们使模型能够更好地适应复杂模式，从而有助于时间序列异常检测的有效性。

6 DISCUSSION

我们进行了全面的实验，表明 PeFAD 在集中式和联合方法方面都优于最先进的基线。结果证明了PLM强大的表示学习能力。此外，所提出的 PPDS 模块还提高了 FL 下的稳定性。消融研究进一步验证了 PeFAD 三个主要组成部分（即 PLM、ADMS 和 PPDS）的有效性。具体来说，ADMS 策略通过捕获块内和块间动态变化，使模型更加关注时间序列中的变化区域。由于时间序列经常随着时间的演变而频繁变化，增强模型学习此类变化的能力可以促进所提出的模型学习代表性特征。此外，PPDS机制帮助模型实现更加一致的客户端更新，从而提高聚合全局模型的性能和稳定性。此外，我们还验证了所提出的高效调优策略有效地减少了通信开销。

在这里插入图片描述

7 CONCLUSION

这项工作提出了 PeFAD，一种用于时间序列异常检测的联邦学习框架。与以前的方法不同，我们的目标是利用预训练语言模型的通用知识和上下文理解能力来解决数据稀缺问题。为了减轻 PLM 带来的联邦学习中的通信和计算负担，我们提出了一种参数高效的联邦训练模块，其中客户端只需要微调和传输小规模参数。此外，PeFAD 采用了一种新颖的异常驱动掩模选择策略来提高时间序列重建的质量，从而提高异常检测的鲁棒性。为了解决客户端异构性问题，还提出了一种保护隐私的共享数据集合成机制，使客户端能够学习到更加一致和全面的信息。对四个真实工作数据集的广泛实验表明了所提出的 PeFAD 的有效性和效率。