180至500公里高度之间的空间物体的矢量化轨道衰减研究（Matlab代码实现）

最新推荐文章于 2025-05-24 21:18:27 发布

荔枝科研社

最新推荐文章于 2025-05-24 21:18:27 发布

阅读量991

点赞数 11

文章标签： matlab 开发语言

本文链接：https://blog.csdn.net/weixin_46039719/article/details/144063164

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、文章

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

摘要：低地球轨道卫星的衰变是许多人感兴趣的问题。这种拖曳力卫星的体验是由于它与这些高度上存在的少数空气分子的相互作用。密度低地球轨道高度的大气层是由太阳X射线通量和磁层粒子沉降控制的因此，它随着当前的空间天气条件而变化。
本文提出了一个简单的模型，将大气密度作为空间环境参数的函数，以及显示了如何应用此方法计算基本圆形轨道上卫星的衰变率和轨道寿命低于500公里高度。本文介绍了一个用QBASIC编写的计算机程序，展示了如何实现该模型。
1.导言
低地球轨道卫星会经历轨道衰变，其物理寿命几乎完全由它们与大气的相互作用。预测此类寿命或重返日期对卫星来说非常重要规划者、使用者、跟踪者，以及经常面向公众。
卫星寿命的预测取决于对初始卫星轨道参数、卫星质量与横截面积（在行进方向上）的比值，以及上层大气密度和如何这响应了也必须预测的空间环境参数。即使有一个完整的大气模型来描述随时间、季节、纬度和高度变化的情况由于卫星姿态预测的不确定性（这影响相关的横截面积），以及太阳和地磁指数（它们会显著改变大气模型）。即使已知大部分数量，似乎仍有一个不可减少的水平，低于这个水平就不可能预测。无论卫星的剩余寿命是多少，这个水平似乎都约为剩余寿命的10%。换句话说，预测一颗预计将在空中停留约10年的卫星衰减的误差为一年，而预计在24小时内重新进入的卫星的消亡时间仅精确到大约2小时！请注意这些数字不适用于航天飞机等航天器，因为航天飞机可以控制重返地球大气层气氛。1979年4月，北美防空司令部对预计的返回进行了预测，从中可以看出对不确定性的认识当年6月11日至7月1日，SKYLAB空间站。实际重返发生在7月11日，在规定区间，中间区间的预测误差约为15%。鉴于在相对较短的时期内出现的此类错误根据预测，大型复杂大气模型中采用的细节与实际大气模型之间存在严重不匹配预测程序和作为输入的预测空间环境参数的准确性。在the在下一节中，将描述一个非常简单的大气模型，该模型乎与精度更接近其他变量中的不确定性对卫星寿命预测的限制。
2. 大大气模型
这种大气模型以及预测方案仅限于轨道完全低于大约500公里的高度。这种轨道可以视为基本圆形，使用半长轴轨道半径的位置。大气密度ρ由一个简单的指数函数指定，具有可变尺度高度
H.对于固定的外逸层温度T，通过使用有效热辐射系数，使H随高度h变化大气分子质量m。该m包括分子质量随高度的实际变化和在180至500公里的考虑范围内，温度变化的补偿期限由于空间环境导致的密度是通过T引入的，T被指定为太阳射电通量的函数F10.7和地磁指数Ap。

📚2 运行结果

部分代码：

%% Inputs:
%
% a [1 x N]/double Semi-Major Axis (km)
%
% e [1 x N]/double Eccentricity
%
% A [1 x N]/double Effective Area (m^2)
%
% Cd [1 x N]/double Coefficient of Drag
%
% m0 [1 x N]/double Satellite Mass (kg)
%
% F107 [1 x N]/double F10.7 Solar Radio Flux
%
% Ap [1 x N]/double Geomagnetic Index
%
%
%% Outputs:
% P [M x N] Orbital Period (sec)
%
% t [M x N] Time of Propagation
% (sec)
%% Revision History:
% Darin C. Koblick (c) 02-12-2016
%% ----------------------------- Begin Code Sequence ----------------------
if exist('getConst','file')
const = getConst();
Re = const.Earth.Rad; %Earth Radius (km)
Mu = const.Earth.Mu; %Earth's Gravitational Constant
else
Re = 6378.137;
Mu = 398600.4418;
end

%% Demonstration of Decay in absense of any user inputs:
if nargin == 0
a = Re+(300:25:400); %km
m0 = 100; %kg
A = 1; %m^2
e = 0;
Cd = 1;
F107 = 70;
Ap = 0;
[P,t] = computeOrbitalDecay(a,e,A,Cd,m0,F107,Ap);
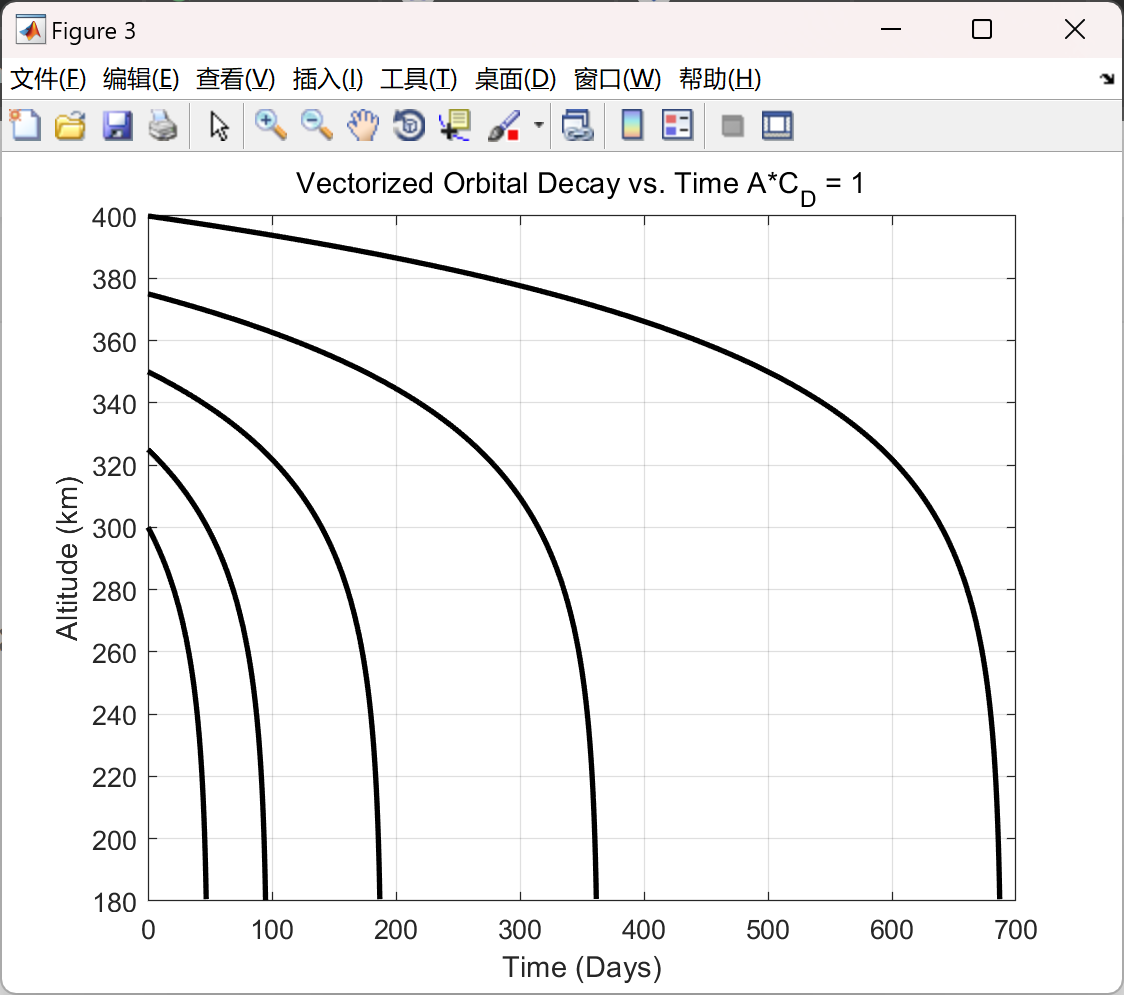
figure('color',[1 1 1]);
plot(t./86400,((P./(2.*pi)).^2.*Mu).^(1/3)-Re,'k','linewidth',2);
grid on;
xlabel('Time (Days)');
ylabel('Altitude (km)');
title(['Vectorized Orbital Decay vs. Time ','A*C_D = ',num2str(A*Cd)]);
ylim([180 max(a-Re)]);
[P,t] = deal([]);
return;
end

P = 2*pi.*sqrt(a.^3./Mu); %Orbital Period (sec)
Ae = A.*Cd; %Effective Cross Sectional Area
dt = min(0.5*P); %Time step in seconds
t = 0; %Elapsed Propagation Time (sec)

%% Defined inline Orbital Routines:
h = @(P)((P./(2.*pi)).^2.*Mu).^(1/3)-Re; % Compute the circular height (km)
rP = @(a,e)a.*(1-e); % Compute the Perigee Radius calculation
he = @(a,e)(rP(a,e)-Re)+900.*e.^(0.6); % Compute the effective height (km)

%% Very Basic Atmospheric Model:
m = @(h)27-0.012.*(h-200); %180 < h [km] < 500
H = @(h)(900 + 2.5.*(F107-70) + 1.5.*Ap)./m(h); %Equivilent height in km
rho = @(h)6e-10.*exp(-(h-175)./H(h)); %Density (kg m^-3)

%% Find the period corresponding to a height of 180 km:
P_min = 2*pi.*sqrt((Re+180).^3./Mu);