💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
永磁直线同步发电机(PMLSM)在起伏浮标波浪能转换器(PA-WEC)中的应用与性能分析
💥1 概述
摘要:海洋波能转换是一个热门的研究领域,因为非可再生能源资源日益稀缺。然而,提取波能并不是一个简单的过程。例如,设计和建造可靠、耐用、高效的波能收集设备是一个挑战。

全文目录:

本报告描述了一个永磁线性同步发电机模型,它是将海洋波能转换成电能的系统的一部分。基于引用文献[2],开发了这种发电机的动态数学模型,并使用多种模拟进行了测试。同步发电机是指所产生电压的波形与发电机的旋转同步的发电机。永磁体用于提供线性同步发电机的场激励。由于机械约束,线性电机具有大的、可变的气隙[3]。因此,磁路具有较大的磁阻。磁阻或磁电阻是磁路的一种属性。磁阻的概念类似于电路中的电阻。但是,磁阻不是消耗电能,而是存储磁能。电场使电流沿最小阻力路径流动。同样,磁场使磁通沿最小磁阻路径流动。永磁体线性同步电机需要具有大的矫顽力的磁铁,矫顽力是将材料磁化饱和后,要将该材料的磁化降为零所需的磁场强度。当材料具有大的矫顽力时,它就难以磁化。
本报告介绍了永磁线性同步发电机模型,该模型是将海洋波能转换成电能系统的一部分。基于引用文献[2],开发了该发电机的动态数学模型,并进行了多种模拟测试。同步发电机的电压波形与发电机旋转同步。永磁体用于提供线性同步发电机的场激励。由于机械限制,线性电机具有大的、可变的气隙[3],因此磁路具有较大的磁阻。磁阻是磁路的一种属性,类似于电路中的电阻。但是,磁阻存储磁能而不是消耗电能。电场使电流沿最小阻力路径流动,磁场使磁通沿最小磁阻路径流动。永磁体线性同步电机需要具有大的矫顽力的磁铁,即在将材料磁化饱和后,要将该材料的磁化降为零所需的磁场强度。
永磁直线同步发电机(PMLSM)在起伏浮标波浪能转换器(PA-WEC)中的应用与性能分析
一、永磁直线同步发电机的结构与优势
-
基本结构与磁场增强设计
永磁直线同步发电机(PMLSM)由初级(定子)和次级(动子)组成,采用Halbach磁极阵列优化磁场分布,显著提升气隙磁密和功率密度。这种设计通过增强磁场强度,可提高电动势幅值并降低谐波畸变率,适用于波浪能转换器(WEC)中的往复运动场景。 -
性能优势
- 高效率与直接驱动:PMLSM无需中间传动机构,直接将浮标的直线运动转换为电能,减少能量损失,效率可达85%以上。
- 动态响应快:通过磁场模型和电路模型的耦合设计,PMLSM能够快速响应波浪频率变化,适应规则波、不规则波甚至极端波况。
- 控制灵活性:采用最大功率点跟踪(MPPT)控制策略和力控制算法,实时优化能量捕获效率。
二、起伏浮标波浪能转换器的取力器(PTO)功能定位
-
取力器的作用
PTO系统是PA-WEC的核心组件,负责将浮标的机械运动(如液压动能或直线动能)转换为电能。传统液压PTO存在效率低(约50%)、维护复杂等问题,而PMLSM作为直接驱动型PTO,可简化结构并提升转换效率至60%-80%。 -
性能评价指标
- 能量转换效率:重点关注波浪能到电能的总效率,包括机械耦合效率与发电效率。
- 峰值与平均功率比:低峰均比(如3:1)表明系统设计匹配波况,减少电网接入的波动性。
- 动态稳定性:在极端波况下(如浪高>4m),需评估PMLSM的磁场退磁风险及机械支撑系统的可靠性。
- 环境适应性:抗腐蚀设计(如永磁体密封)和耐冲击性能是关键。
三、系统建模与优化方法
-
多物理场耦合建模
- 水动力模型:基于势流理论或计算流体力学(CFD)模拟浮标的运动响应。
- 机电耦合模型:结合磁场模型(如有限元分析)与电路模型,预测PMLSM的输出特性。
- 控制模型:采用滑模变结构控制或模型预测控制(MPC),优化动态响应。
-
参数优化技术
- 多目标优化算法:遗传粒子群综合算法(GAPSO)用于平衡磁场强度与机械强度,降低制造成本。
- 实验验证:通过样机台架测试,验证Halbach阵列对谐波抑制的效果(可降低谐波畸变率至5%以下)。
四、技术难点与解决方案
-
低速大推力设计
波浪驱动的动子速度通常为0.5-2 m/s,需通过优化永磁体布局(如横向磁通结构)和绕组设计提升推力密度(目标>5 kN/m²)。 -
多物理场耦合挑战
- 磁场与机械振动耦合:采用磁-机联合仿真,抑制动子振动对磁场均匀性的影响。
- 热管理:高负载下绕组温升需通过液冷或相变材料散热控制温升<50°C。
-
环境适应性
- 防腐蚀:采用钛合金外壳或陶瓷涂层保护永磁体。
- 密封设计:动子与定子间采用磁流体密封,防止海水侵入。
五、案例分析与前沿技术
-
典型应用案例
- 英国Ceto浮标系统:采用模块化PMLSM设计,单浮标功率输出达150 kW,适用于深水区域。
- 中国鹰式浮标:集成液压-PMLSM混合PTO,在南海测试中实现平均效率65%。
-
前沿技术方向
- 超导材料应用:高温超导直线电机可提升功率密度30%,但需解决低温冷却问题。
- 人工智能控制:基于深度学习的实时波况预测与PTO参数自适应调整,可提升极端波况下的生存率。
六、结论
永磁直线同步发电机作为起伏浮标波浪能转换器的取力器,凭借其高效率、直接驱动和动态响应优势,已成为替代传统液压系统的优选方案。未来研究需进一步解决低速推力密度提升、环境适应性和多物理场耦合问题,同时探索超导材料与智能控制技术的融合应用,以实现波浪能商业化开发的突破。
📚2 运行结果

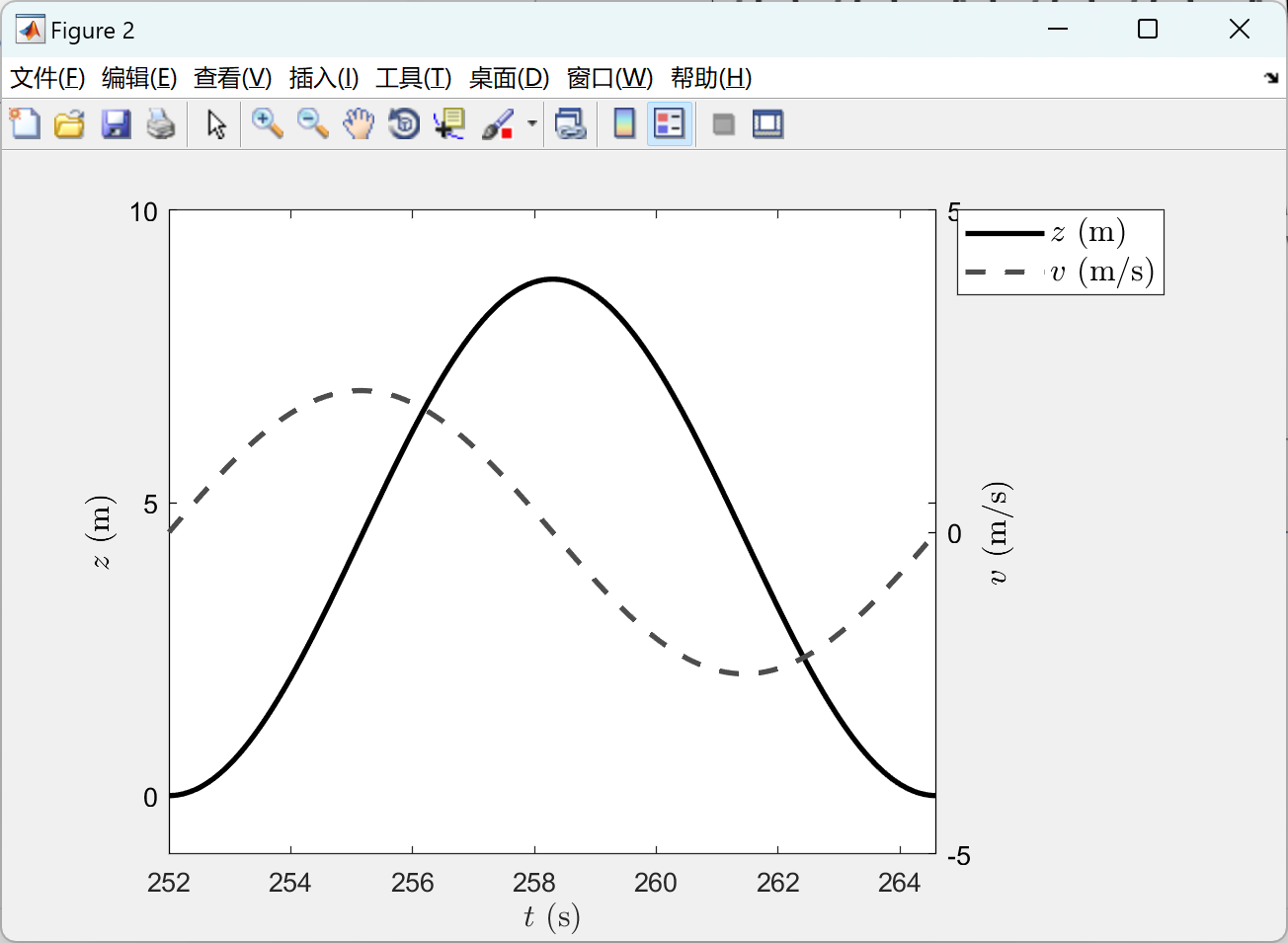


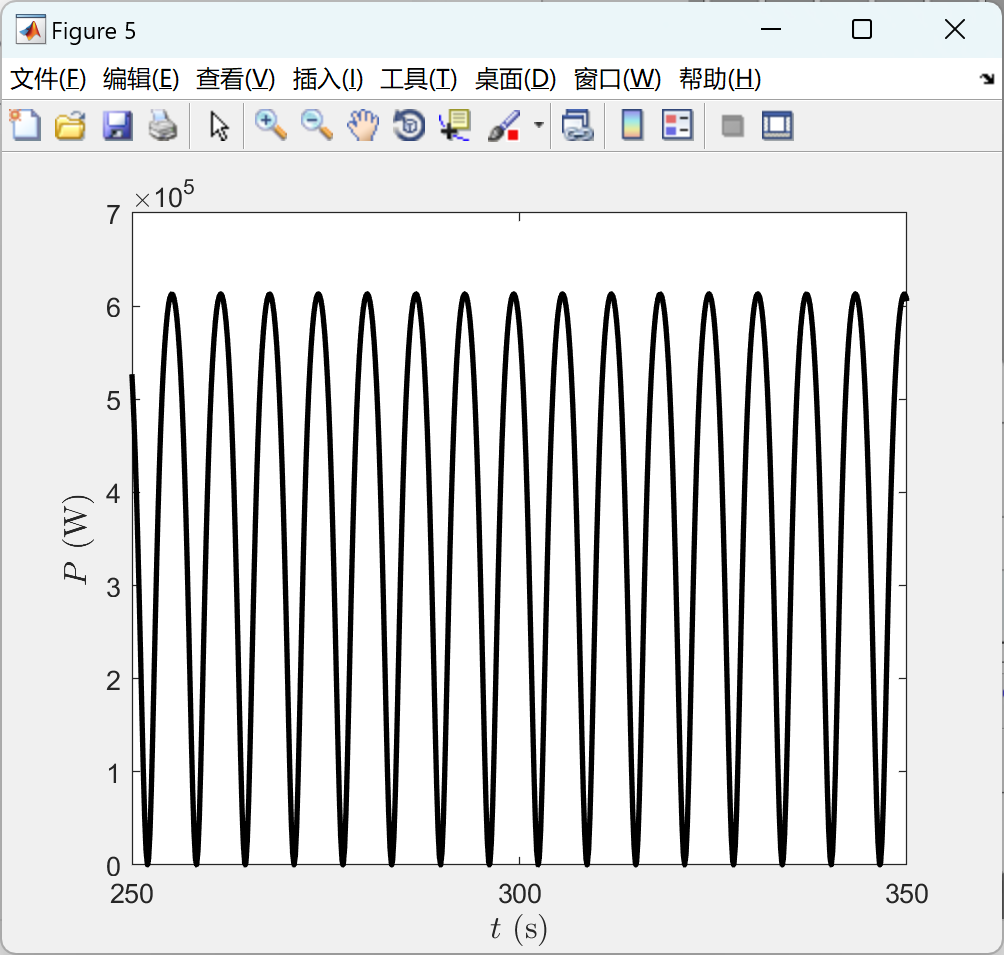

部分代码:
%% figure // Current-Complex-Zoom
data.fig_name = 'Current-Complex-Zoom';
% label names
data.xname = '$t$ (s)';
data.yname = '$i$ (A)';
data.y1name = '$i_1$ (A)';
data.y2name = '$i_2$ (A)';
data.y3name = '$i_3$ (A)';
% state data
data.x1 = t;
data.y1 = x(:,3); % current 1
data.y2 = x(:,4); % current 2
data.y3 = x(:,5); % current 3
% axis limits
data.xmin = 255.2;
data.xmax = 267.8;
data.ymin = -300;
data.ymax = 300;
fig_index = fig_index + 1;
create_figure(data,fig_index,3)
save2pdf(strcat(path,data.fig_name,'.pdf'),fig_index,600)
%% figure // Power-Complex
data.fig_name = 'Power-Complex';
% label names
data.xname = '$t$ (s)';
data.yname = '$P$ (W)';
% state data
data.x1 = t;
data.y1 = Pout; % power
% axis limits
data.xmin = 250;
data.xmax = 350;
data.ymin = 0;
data.ymax = 7*10^5;
fig_index = fig_index + 1;
create_figure(data,fig_index,1)
save2pdf(strcat(path,data.fig_name,'.pdf'),fig_index,600)
%% figure // Power-Complex-Zoom
data.fig_name = 'Power-Complex-Zoom';
% label names
data.xname = '$t$ (s)';
data.yname = '$P$ (W)';
% state data
data.x1 = t;
data.y1 = Pout; % power
% axis limits
data.xmin = 255.2;
data.xmax = 267.8;
data.ymin = 0;
data.ymax = 7*10^5;
fig_index = fig_index + 1;
create_figure(data,fig_index,1)
save2pdf(strcat(path,data.fig_name,'.pdf'),fig_index,600)
%% figure // Timestep-Complex
delta = zeros(length(t) - 1,1);
n = 1:length(t) - 1;
for i = 1:length(t) - 1
delta(i) = t(i + 1) - t(i);
end
data.fig_name = 'Timestep-Complex';
% label names
data.xname = '$i$';
data.yname = 'log$_{10}(\Delta t)$';
% state data
data.x1 = n;
data.y1 = log10(delta); % power
% axis limits
data.xmin = 0;
data.xmax = 60000;
data.ymin = -3.5;
data.ymax = -1;
fig_index = fig_index + 1;
create_figure(data,fig_index,1)
save2pdf(strcat(path,data.fig_name,'.pdf'),fig_index,600)
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。

























 591
591

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










